luogu P3355 骑士共存问题 |最大流

题目描述

在一个 \(n*n\)个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入

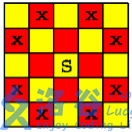
对于给定的 \(n*n\) 个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击

输入格式

第一行有 2 个正整数\(n\) 和 \(m\) \((1<=n<=200, 0<=m<n^2)\)，分别表示棋盘的大小和障碍数。接下来的 \(m\) 行给出障碍的位置。每行 \(2\) 个正整数，表示障碍的方格坐标。

输出格式

将计算出的共存骑士数输出

---

将棋盘上的点分成两类，求最小割

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define int long long
#define ll long long
#define re register int
using namespace std;
const int N=4e5+10,M=6e5+10,inf=1<<30;
int n,m,s,t,maxflow;
int nxt[M],head[N],go[M],edge[M],tot=1;
inline void add(int u,int v,int o){
	nxt[++tot]=head[u];head[u]=tot;go[tot]=v;edge[tot]=o;
	nxt[++tot]=head[v];head[v]=tot;go[tot]=u;edge[tot]=0;	
}
int d[N];
inline bool bfs(){
	queue<int>q;
	memset(d,0,sizeof(d));
	q.push(s);d[s]=1;
	while(q.size()){
		int u=q.front();q.pop();
		for(re i=head[u];i;i=nxt[i]){
			int v=go[i];
			if(edge[i]&&!d[v]){
				q.push(v);
				d[v]=d[u]+1;
				if(v==t)return 1;
			}
		}
	}
	return 0;
}
inline int dinic(int u,int flow){
	if(u==t)return flow;
	int rest=flow,k;
	for(re i=head[u];i&&rest;i=nxt[i]){
		int v=go[i];
		if(edge[i]&&d[v]==d[u]+1){
			k=dinic(v,min(rest,edge[i]));
			if(!k)d[v]=0;
			edge[i]-=k;
			edge[i^1]+=k;
			rest-=k;
		}
	}
	return flow-rest;
}
bool vis[205][205];
inline int P(int x,int y){
    return (x-1)*n+y;
}
const int dx[8]={1,1,-1,-1,2,2,-2,-2},dy[8]={2,-2,2,-2,1,-1,1,-1}; 
signed main(){
    cin>>n>>m; t=n*n+2;
    for(int i=1,x,y;i<=m;i++){
        scanf("%lld%lld",&x,&y);
        vis[x][y]=1;
    }
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++){
        if(!vis[i][j]){
            if((i+j)&1)add(s,P(i,j),1);
            else add(P(i,j),t,1);
        }
        if((i+j)&1)
        for(int k=0;k<8;k++){
            int x=i+dx[k],y=j+dy[k];
            if(x<1||y<1||x>n||y>n||vis[x][y])continue;
            add(P(i,j),P(x,y),inf);
        }
    }
	int flow=0;
	while(bfs())
	while(flow=dinic(s,inf))maxflow+=flow;
	cout<<n*n-m-maxflow<<endl;
}