题解 七十
弄个矩阵高斯消元
发现矩阵很像带状矩阵
具体一点,它长这样:

那么一种处理方式是分成几个部分分别处理
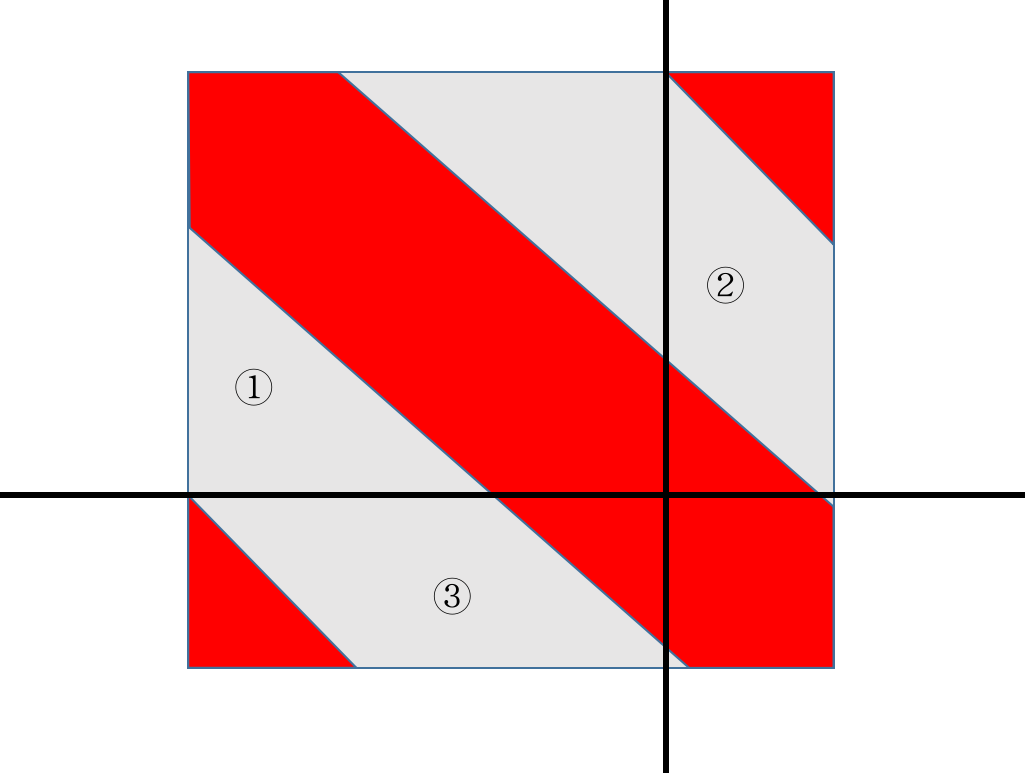
先把 2 部分当成增广部分(用这部分未知数表示前 \(n-k\) 个元)
然后把 1 部分消成只有主对角线上有值
然后用 1 部分将 3 部分消空(右边仍当做增广矩阵)
然后对 4 部分暴力消元,消的时候把区域 2 也消空
这样的话复杂度是 \(O(nk^2+k^3)\) 的
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define N 20010
#define ll long long
//#define int long long
char buf[1<<21], *p1=buf, *p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf, 1, 1<<21, stdin)), p1==p2?EOF:*p1++)
inline int read() {
int ans=0, f=1; char c=getchar();
while (!isdigit(c)) {if (c=='-') f=-f; c=getchar();}
while (isdigit(c)) {ans=(ans<<3)+(ans<<1)+(c^48); c=getchar();}
return ans*f;
}
int n, k;
ll l[N][55], r[N][55], sum[N];
const ll mod=998244353;
inline void add(ll& a, ll b) {a=(a+b)%mod;}
inline void mul(ll& a, ll b) {a=a*b%mod;}
inline ll qpow(ll a, ll b) {ll ans=1; for (; b; a=a*a%mod,b>>=1) if (b&1) ans=ans*a%mod; return ans;}
namespace force{
ll ans[N];
struct matrix{
int n, m;
ll a[310][310];
void resize(int x, int y) {n=x; m=y; memset(a, 0, sizeof(a));}
inline ll* operator [] (int t) {return a[t];}
void put() {for (int i=0; i<=n; ++i) {for (int j=0; j<=m; ++j) cout<<setw(10)<<a[i][j]<<' '; cout<<endl;}cout<<endl;}
void gauss() {
for (int i=0; i<n; ++i) {
int r=i;
while (r<=n && !a[r][i]) ++r;
swap(a[i], a[r]);
ll t=qpow(a[i][i], mod-2);
for (int j=i; j<=m; ++j) a[i][j]=a[i][j]*t%mod;
for (int j=0; j<=n; ++j) if (j!=i) {
ll t=a[j][i];
for (int k=i; k<=m; ++k) a[j][k]=(a[j][k]-a[i][k]*t)%mod;
}
}
for (int i=0; i<n; ++i) ans[i]=a[i][m];
}
}f;
void solve() {
f.resize(n, n);
for (int i=0; i<n; ++i) {
f[i][i]=-1;
ll inv=qpow(sum[i], mod-2);
for (int j=1; j<=k; ++j) f[(i-j+n)%n][i]=(f[(i-j+n)%n][i]+l[i][j]*inv)%mod;
for (int j=1; j<=k; ++j) f[(i+j)%n][i]=(f[(i+j)%n][i]+r[i][j]*inv)%mod;
}
for (int i=0; i<=n; ++i) f[n][i]=1;
f.gauss();
for (int i=0; i<n; ++i) printf("%lld\n", (ans[i]%mod+mod)%mod);
}
}
namespace task1{
ll kl[N], kr[N], k[N], f[N], inv[N];
void solve() {
for (int i=0; i<n; ++i) inv[i]=qpow(sum[i], mod-2);
kl[0]=k[0]=1;
for (int i=1; i<n; ++i) {
ll t=(1-kr[i-1]*r[i-1][1]%mod*inv[i-1]%mod)%mod;
kl[i]=kl[i-1]*r[i-1][1]%mod*inv[i-1]%mod*qpow(t, mod-2)%mod;
kr[i]=l[(i+1)%n][1]*inv[(i+1)%n]%mod*qpow(t, mod-2)%mod;
}
for (int i=n-1; i; --i) k[i]=(kl[i]+kr[i]*k[(i+1)%n])%mod;
ll sum=0;
for (int i=0; i<n; ++i) sum=(sum+k[i])%mod;
f[0]=qpow(sum, mod-2);
for (int i=1; i<n; ++i) f[i]=f[0]*k[i]%mod;
for (int i=0; i<n; ++i) printf("%lld\n", (f[i]%mod+mod)%mod);
}
}
namespace task{
ll ans[N];
int size, cnt;
struct node{ll val; int next, dat;}e[N*5000];
unordered_map<int, ll> mp[N];
struct matrix{
int n, m;
struct array{
int id, n, m;
ll a[165];
inline ll& operator [] (int t) {
if (id>=n-k) return mp[id][t];
if (t>=max(id-k, 0)&&t<=min(id+k, m-k-1)) return a[t-(id-k)];
else if (t>=m-k) return a[105+t-(m-k)];
else return a[164];
}
}a[N];
// struct hash_map{
// static const int SIZE=55;
// int head[SIZE], sta[SIZE], top;
// hash_map(){memset(head, -1, sizeof(head));}
// inline int end() {return -1;}
// inline ll& operator [] (int t) {
// int t2=1ll*t*98244353%SIZE;
// if (head[t2]==-1) sta[++top]=t2;
// for (int i=head[t2]; ~i; i=e[i].next)
// if (e[i].dat==t) return e[i].val;
// e[++size]={0, head[t2], t}; head[t2]=size;
// return e[size].val;
// }
// inline int find(int t) {
// int t2=1ll*t*98244353%SIZE;
// for (int i=head[t2]; ~i; i=e[i].next)
// if (e[i].dat==t) return 1;
// return -1;
// }
// void clear() {
// while (top) head[sta[top--]]=-1;
// size=0;
// }
// }a[N];
// void resize(int x, int y) {n=x; m=y;}
void resize(int x, int y) {n=x; m=y; for (int i=0; i<=n; ++i) a[i].id=i, a[i].n=x, a[i].m=y;}
inline array& operator [] (int t) {return a[t];}
// inline hash_map& operator [] (int t) {return a[t];}
// inline unordered_map<int, ll>& operator [] (int t) {return a[t];}
void put() {for (int i=0; i<=n; ++i) {for (int j=0; j<=m; ++j) cout<<setw(10)<<a[i][j]<<' '; cout<<endl;}cout<<endl;}
void gauss() {
for (int i=0; i<n-k; ++i) {
ll t=qpow(a[i][i], mod-2); ++cnt;
for (int j=i; j<=min(i+k, m-k-1); ++j) mul(a[i][j], t), ++cnt;
for (int j=m-k; j<=m; ++j) mul(a[i][j], t), ++cnt;
for (int j=i+1; j<=min(i+k, n-k-1); ++j) {
ll d=a[j][i]; ++cnt;
for (int t=i; t<=min(i+k, m-k-1); ++t) add(a[j][t], -a[i][t]*d), cnt+=2;
for (int t=m-k; t<=m; ++t) add(a[j][t], -a[i][t]*d), cnt+=2;
}
}
for (int i=n-k-1; ~i; --i) {
for (int j=max(i-k, 0); j<i; ++j) {
ll d=a[j][i];
// if (j<i-k) assert(!d);
for (int t=i; t<=min(i+k, m-k-1); ++t) add(a[j][t], -a[i][t]*d);
for (int t=m-k; t<=m; ++t) add(a[j][t], -a[i][t]*d);
}
}
for (int i=0; i<n-k; ++i) {
for (int j=n-k; j<=n; ++j) {
ll d=a[j][i]; a[j][i]=0;
for (int t=m-k; t<=m; ++t) add(a[j][t], -a[i][t]*d);
}
}
for (int i=n-k; i<=n; ++i) {
int r=i;
while (r<=n && !a[r][i]) ++r;
// swap(a[i], a[r]);
swap(mp[i], mp[r]);
ll t=qpow(a[i][i], mod-2);
for (int j=i; j<=m; ++j) mul(a[i][j], t);
for (int j=0; j<=n; ++j) if (j!=i) {
ll d=a[j][i];
for (int t=i; t<=m; ++t) add(a[j][t], -a[i][t]*d);
}
}
for (int i=0; i<n; ++i) ans[i]=a[i][m];
}
}f;
void solve() {
f.resize(n, n);
for (int i=0; i<n; ++i) {
f[i][i]=-1;
ll inv=qpow(sum[i], mod-2);
for (int j=1; j<=k; ++j) f[(i-j+n)%n][i]=(f[(i-j+n)%n][i]+l[i][j]*inv)%mod;
for (int j=1; j<=k; ++j) f[(i+j)%n][i]=(f[(i+j)%n][i]+r[i][j]*inv)%mod;
}
for (int i=0; i<=n; ++i) f[n][i]=1;
f.gauss();
// f.put();
cerr<<"cnt: "<<cnt<<endl;
for (int i=0; i<n; ++i) printf("%lld\n", (ans[i]%mod+mod)%mod);
}
}
signed main()
{
freopen("seventy.in", "r", stdin);
freopen("seventy.out", "w", stdout);
n=read(); k=read();
for (int i=0; i<n; ++i) {
for (int j=k; j; --j) sum[i]=(sum[i]+(l[i][j]=read()))%mod;
for (int j=1; j<=k; ++j) sum[i]=(sum[i]+(r[i][j]=read()))%mod;
}
// if (k==1) task1::solve();
// force::solve();
task::solve();
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号