题解 DZY Loves Math IV/P4240 毒瘤之神的考验/暴力题

DZY Loves Math IV
P4240 毒瘤之神的考验
暴力题

不知道之前 DZY 这题我为什么没写题解大概是忘了，所以先来补一下
因为 \(m\leqslant 1e9\)，所以推法和后面并不太一样
令 \(p=\prod p_i^{c_i-1},q=\prod p_i\)

\[\begin{aligned} S(n, m)&=p\sum\limits_{i=1}^m\varphi(iq)\\ &=p\sum\limits_{i=1}^m\varphi(\frac{q}{\gcd(i, q)}\times i\times\gcd(i, q))\\ &=p\sum\limits_{i=1}^m\varphi(\frac{q}{\gcd(i, q)})\times \varphi(i\times\gcd(i, q))\\ &=p\sum\limits_{i=1}^m\varphi(\frac{q}{\gcd(i, q)})\times \varphi(i)\times\gcd(i, q)\\ &=p\sum\limits_{i=1}^m\varphi(\frac{q}{\gcd(i, q)})\times \varphi(i)\times\sum\limits_{d\mid\gcd(i, q)}\varphi(d)\\ &=p\sum\limits_{i=1}^m\varphi(i)\times\sum\limits_{d\mid\gcd(i, q)}\varphi(\frac{q}{d})\\ &=p\sum\limits_{d\mid q}\varphi(\frac{q}{d})\sum\limits_{i=1}^{\lfloor\frac{m}{d}\rfloor}\varphi(id)\\ &=p\sum\limits_{d\mid q}\varphi(\frac{q}{d})S(d, \lfloor\frac{m}{d}\rfloor)\\ \end{aligned}\]

边界为 \(n=1\) 时杜教筛，复杂度证明见这里

然后是 P4240 毒瘤之神的考验
发现现在 \(n, m\leqslant 1e5\)，但有 \(1e4\) 组多测
式子太长了不想手打一遍了


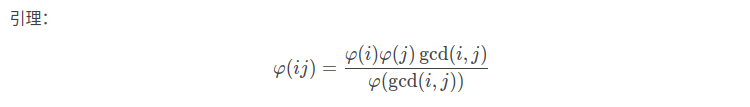
令 \(f(x)=\sum\limits_{d\mid x}\frac{d}{\varphi(d)}\mu(\frac{x}{d})\)
令 \(g(y, x)=\sum\limits_{i=1}^x\varphi(iy)\)，有 \(g(y, x)=g(y, x-1)+\varphi(xy)\)
令 \(h(x, y, z)=\sum\limits_{i=1}^zf(i)g(i, x)g(i, y)\)，有 \(h(x, y, z)=h(x, y, z-1)+f(z)g(z, x)g(z, y)\)
这里 \(f\) 和 \(g\) 可以 \(O(n\ln n)\) 预处理出来
然后考虑根号分治
\(h\) 可以 \(O(nB^2)\) 预处理出 \(\frac{m}{T}\leqslant B\) 的部分
剩下的部分有 \(T\leqslant\frac{m}{B}\)，暴力算即可

点击查看代码

#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define N 100010
#define ll long long
//#define int long long

char buf[1<<21], *p1=buf, *p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf, 1, 1<<21, stdin)), p1==p2?EOF:*p1++)
inline int read() {
	int ans=0, f=1; char c=getchar();
	while (!isdigit(c)) {if (c=='-') f=-f; c=getchar();}
	while (isdigit(c)) {ans=(ans<<3)+(ans<<1)+(c^48); c=getchar();}
	return ans*f;
}

int n, m;
bool npri[N];
ll f[N], invphi[N];
vector<ll> g[N];
vector<ll> h[55][55];
const int len=50;
int pri[N], mu[N], phi[N], pcnt;
const ll mod=998244353;
inline ll qpow(ll a, ll b) {ll ans=1; for (; b; a=a*a%mod,b>>=1) if (b&1) ans=ans*a%mod; return ans;}

void init() {
	mu[1]=phi[1]=1;
	for (int i=2; i<N; ++i) {
		if (!npri[i]) pri[++pcnt]=i, phi[i]=i-1, mu[i]=-1;
		for (int j=1,x; j<=pcnt&&i*pri[j]<N; ++j) {
			npri[x=i*pri[j]]=1;
			if (!(i%pri[j])) {phi[x]=phi[i]*pri[j]; break;}
			else phi[x]=phi[i]*phi[pri[j]], mu[x]=-mu[i];
		}
	}
	for (int i=1; i<N; ++i) invphi[i]=qpow(phi[i], mod-2);
	for (int i=1; i<N; ++i)
		for (int j=i; j<N; j+=i)
			f[j]=(f[j]+i*invphi[i]*mu[j/i])%mod;
	for (int i=1; i<N; ++i) {
		g[i].resize(N/i+1);
		for (int j=1,lim=N/i; j<=lim; ++j)
			g[i][j]=(g[i][j-1]+phi[i*j])%mod;
	}
	for (int i=1; i<=len; ++i)
		for (int j=1; j<=len; ++j) {
			h[i][j].resize((N-1)/max(i, j)+1);
			for (int k=1,lim=(N-1)/max(i, j); k<=lim; ++k)
				h[i][j][k]=(h[i][j][k-1]+f[k]*g[k][i]%mod*g[k][j])%mod;
		}
}

ll solve(int n, int m) {
	if (n>m) swap(n, m);
	ll ans=0;
	// for (int t=1; t<=n; ++t) ans=(ans+f[t]*g[t][n/t]%mod*g[t][m/t])%mod;
	int lim=m/len;
	for (int t=1; t<=lim; ++t) ans=(ans+f[t]*g[t][n/t]%mod*g[t][m/t])%mod;
	for (int l=lim+1,r; l<=n; l=r+1) {
		r=min(n/(n/l), m/(m/l));
		ans=(ans+h[n/l][m/l][r]-h[n/l][m/l][l-1])%mod;
	}
	return (ans%mod+mod)%mod;
}

signed main()
{
	// freopen("b.in", "r", stdin);
	// freopen("b.out", "w", stdout);

	int T=read();
	init();
	while (T--) {
		n=read(); m=read();
		printf("%lld\n", solve(n, m));
	}
	
	return 0;
}