题解 如何优雅的送分

传送门

我只知道如何优雅的爆零

• 当计数题让算形如 \(2^{f(i)}\) 的柿子时，（尤其当 \(f(i)\) 为一个计数函数）特别注意也许可以理解为对所有情况枚举子集
  可以考虑设法对合法的子集进行计数
• \(\mu^2(i)\) 的实际意义是 \(i\) 这个数是否不含平方因子

于是这题就可以转化为对每个数中含有的质因子的子集进行计数
首先有

\[ans=\sum\limits_{i=1}^n \mu^2(i)\lfloor\frac{n}{i}\rfloor \]

这里 \(i\) 是在枚举质因子集合，则有 \(\frac{n}{i}\) 个数包含它于是计数

• 关于对 \(\mu\) 函数的平方求前缀和，有
  \[\sum\limits_{i=1}^n\mu^2(i) = \sum\limits_{i=1}^{n}\lfloor\frac{n}{i^2}\rfloor \mu(i) \]
  考虑 \(\mu^2\) 的实际意义是是否不含平方因子
  若一个k含平方因子，且这些平方因子为 \(\{p_1, p_2...p_n\}\)
  \(i\) 依然是在枚举因子集合，一定会枚举到上面集合的子集
  于是若该集合不是空集，所有子集都被枚举后 \(\mu\) 实现了偶加奇减，总贡献为0
  若是空集，将会在 \(i=1\) 处产生恰好一次贡献
  复杂度是根号级别的

但是这样只有部分分，于是还有一种推法：

\[2^{F(n)}=\sum\limits_{d\mid n}\mu^2(d) \]

这里 \(d\) 是在枚举 \(n\) 的所有因子集合
但因为我们在枚举子集的时候要求每个质因子至多出现一次（即不包含平方因子），所以用 \(\mu\) 函数来计数
于是

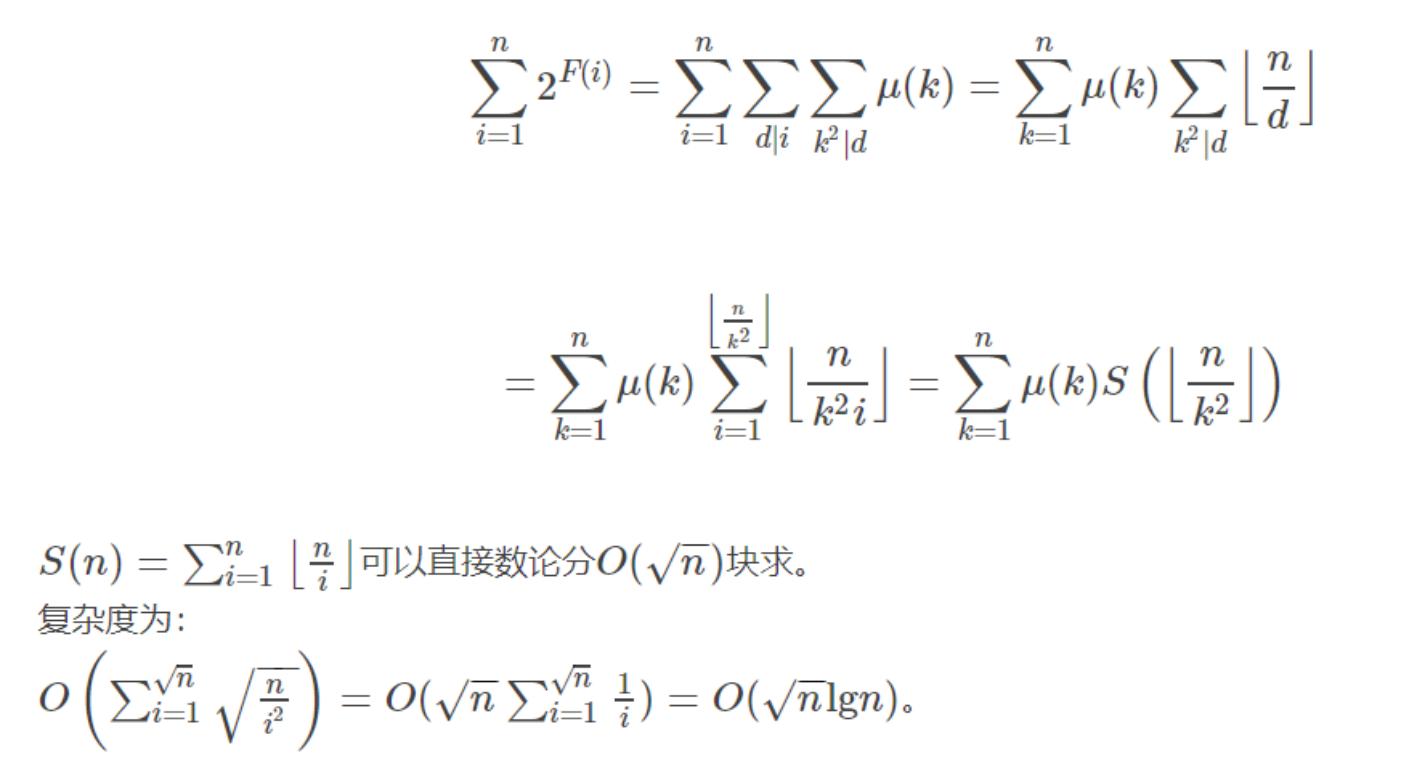
Code:

#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define N 1000010
#define ll long long
//#define int long long

char buf[1<<21], *p1=buf, *p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf, 1, 1<<21, stdin)), p1==p2?EOF:*p1++)
inline ll read() {
	ll ans=0, f=1; char c=getchar();
	while (!isdigit(c)) {if (c=='-') f=-f; c=getchar();}
	while (isdigit(c)) {ans=(ans<<3)+(ans<<1)+(c^48); c=getchar();}
	return ans*f;
}

ll n;
int pri[N], pcnt, f[N], mu[N];
bool npri[N];
const ll mod=1e9+7;
inline ll qpow(ll a, ll b) {ll ans=1ll; for (; b; a=a*a%mod,b>>=1) if (b&1) ans=ans*a%mod; return ans;}

namespace force{
	ll cnt[N], ans;
	void solve() {
		for (int i=1; i<=n; ++i) ++cnt[f[i]];
		for (int i=0; i<=n; ++i) ans=(ans+cnt[i]*qpow(2, i)%mod)%mod;
		printf("%lld\n", ans);
		exit(0);
	}
}

namespace task{
	ll s(ll n) {
		ll ans=0;
		for (ll l=1,r; l<=n; l=r+1) {
			r=(n/(n/l));
			ans=(ans+(r-l+1)*(n/l))%mod;
		}
		return ans;
	}
	void solve() {
		ll sqr=sqrt(n), ans=0;
		for (ll i=1; i<=sqr; ++i) {
			ans=(ans+mu[i]*s(n/(i*i)))%mod;
		}
		printf("%lld\n", (ans%mod+mod)%mod);
		exit(0);
	}
}

signed main()
{
	freopen("elegant.in", "r", stdin);
	freopen("elegant.out", "w", stdout);

	n=read();
	npri[0]=npri[1]=1; mu[1]=1;
	for (int i=2; i<N; ++i) {
		if (!npri[i]) pri[++pcnt]=i, f[i]=1, mu[i]=-1;
		for (int j=1; j<=pcnt&&i*pri[j]<N; ++j) {
			f[i*pri[j]]=f[i]+(i%pri[j]!=0);
			npri[i*pri[j]]=1;
			if (!(i%pri[j])) break;
			else mu[i*pri[j]]=-mu[i];
		}
	}
	// cout<<"n: "; for (int i=1; i<=20; ++i) cout<<setw(2)<<i<<' '; cout<<endl;
	// cout<<"f: "; for (int i=1; i<=20; ++i) cout<<setw(2)<<f[i]<<' '; cout<<endl;
	// force::solve();
	task::solve();

	return 0;
}