题解 高考（留坑）

传送门

• 当出现形如「\(m\) 次操作，每次随机选一个数/人/位置进行一次操作，选中第 \(i\) 个数/人/位置的概率为 \(\frac{a_i}{\sum\limits_{j=1}^n a_j}\) 时，尝试证一下得到每种结果概率都相等」

对于本题，每种情况的概率为

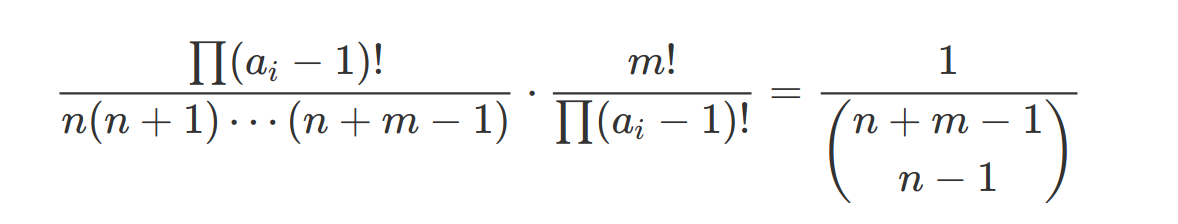
神仙题，感觉理解的不好，先咕着以后补吧

Code:

#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define N 5010
#define ll long long
#define reg register int
// #define int long long

char buf[1<<21], *p1=buf, *p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf, 1, 1<<21, stdin)), p1==p2?EOF:*p1++)
inline int read() {
	int ans=0, f=1; char c=getchar();
	while (!isdigit(c)) {if (c=='-') f=-f; c=getchar();}
	while (isdigit(c)) {ans=(ans<<3)+(ans<<1)+(c^48); c=getchar();}
	return ans*f;
}

int n, m;
const ll mod=1e9+7;
inline void md(ll& a, ll b) {a+=b; a=a>=mod?a-mod:a;}
inline ll qpow(ll a, ll b) {ll ans=1ll; for (; b; a=a*a%mod,b>>=1) if (b&1) ans=ans*a%mod; return ans;}

namespace force{
	ll ans[N], inv[N];
	int a[N], tem[N];
	void dfs(int u, ll pro) {
		// cout<<"a: "; for (int i=1; i<=n; ++i) cout<<a[i]<<' '; cout<<"u: "<<u<<' '<<pro<<endl;
		if (u>m) {
			// cout<<"a: "; for (int i=1; i<=n; ++i) cout<<a[i]<<' '; cout<<"u: "<<u<<' '<<pro<<endl;
			for (int i=1; i<=n; ++i) tem[i]=a[i];
			sort(tem+1, tem+n+1, [](int a, int b) {return a>b;});
			ll sum=0;
			for (int i=1; i<=n; ++i) {
				sum+=tem[i];
				// cout<<"sum: "<<sum<<' '<<sum*pro%mod<<endl;
				ans[i]=(ans[i]+sum*pro%mod)%mod;
			}
			return ;
		}
		for (int i=1; i<=n; ++i) {
			++a[i];
			dfs(u+1, pro*(a[i]-1)%mod*inv[n+u-1]%mod);
			--a[i];
		}
	}
	void solve() {
		inv[0]=inv[1]=1;
		for (int i=2; i<=n+m; ++i) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
		// cout<<"inv: "; for (int i=1; i<=n+m; ++i) cout<<inv[i]<<' '; cout<<endl;
		for (int i=1; i<=n; ++i) a[i]=1;
		dfs(1, 1);
		for (int i=1; i<=n; ++i) printf("%lld\n", ans[i]);
		exit(0);
	}
}

namespace task{
	ll fac[N<<1], inv[N<<1], g[N][N], f[N][N];
	inline ll C(int n, int k) {return fac[n]*inv[k]%mod*inv[n-k]%mod;}
	void solve() {
		int lim=n+m;
		fac[0]=fac[1]=1; inv[0]=inv[1]=1;
		for (int i=2; i<=lim; ++i) fac[i]=fac[i-1]*i%mod;
		for (int i=2; i<=lim; ++i) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
		for (int i=2; i<=lim; ++i) inv[i]=inv[i-1]*inv[i]%mod;
		for (int i=1; i<=n; ++i)
			for (int j=1; i*j<=m; ++j)
				for (int k=i; k<=n&&k*j<=m; ++k)
					g[i][j]=(g[i][j]+C(k, i)*((k-i)&1?-1:1)*C(n, k)%mod*C(m-k*j+n-1, n-1)%mod)%mod;
		ll ans=0;
		for (int i=n; i; --i) 
			for (int j=1; j<=m; ++j)
				f[i][j]=(g[i][j]+f[i+1][j])%mod;
		for (int i=1; i<=n; ++i) {
			for (int j=1; j<=m; ++j)
				ans=(ans+f[i][j])%mod;
			printf("%lld\n", ((ans*qpow(C(n+m-1, n-1), mod-2)%mod+i)%mod+mod)%mod);
		}
		exit(0);
	}
}

signed main()
{
	freopen("c.in", "r", stdin);
	freopen("c.out", "w", stdout);

	n=read(); m=read();
	// force::solve();
	task::solve();

	return 0;
}