题解 DZY Loves Math

传送门

本来以为是大水题，结果做了一天

首先柿子很好化成 \(\sum\limits_{T=1}^n \lfloor \frac{n}{T} \rfloor \lfloor \frac{m}{T} \rfloor \sum\limits_{k \mid T} f(k) * \mu(\frac{T}{k})\)
考虑怎么预处理 \(f\)
发现对于一个 \(i\)，\(f(i*pri_j)\) 的取值只能在 \(f(i)\) 和 \(cnt_{pri_j}\) 之中
所以可以线性筛

这部分线性筛代码

mu[1]=1;
for (reg i=2,cnt,s; i<N; ++i) {
	if (!npri[i]) pri[++pcnt]=i, mu[i]=-1, f[i]=1;
	for (reg j=1; j<=pcnt&&i*pri[j]<N; ++j) {
		npri[i*pri[j]]=1;
		if (!(i%pri[j])) {
			s=i; cnt=1;
			while (!(s%pri[j])) {++cnt; s/=pri[j];}
			f[i*pri[j]]=max2(f[i], cnt);
			break;
		}
		else mu[i*pri[j]]=-mu[i], f[i*pri[j]]=f[i];
	}
}

然后考虑预处理 \(\sum\limits_{k \mid T} f(k) * \mu(\frac{T}{k})\)
大力卡常的话其实可以过
但有 \(O(n)\) 的预处理方法
令 \(h(n) = \sum\limits_{k \mid n} f(k) * \mu(\frac{n}{k})\)
\(f\) 不是积性函数，无法直接线性筛
尝试找找它有什么性质
令 \(T = \prod p_i^{a_i}\) 的话，发现对于一个当前枚举的 \(i = \prod p_i^{b_i}\)
\(i\) 能产生贡献的前提是 \(\mu\) 不为0，也即 \(\forall a_i, b_i\) 有 \(a_i-b_i \in [0, 1]\)
康康这个东西有什么性质
那对于一个固定的 \(T\)，如果它的质因子有 \(k\) 个，就会有 \(2^k\) 个数能对 \(h(T)\) 产生贡献（考虑 \(b_i=a_i\) 或 \(b_i=a_i-1\)）
有一个极其神奇的地方：
截一段大佬博客

对于情况1的理解：

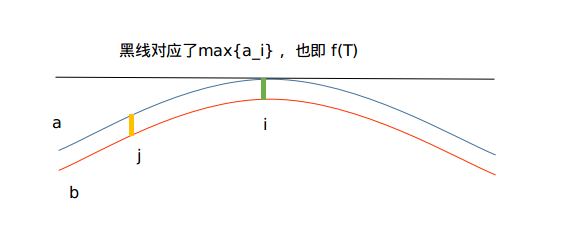
对于这个图上的位置 \(i\)，有01两种选法，对于每一种选法：
注意到位置 \(j\) 无论怎么选都不会影响到 \(f(T)\)
而位置 \(j\) 选0或选1对应的 \(\mu\) 成相反数，所以消掉了

对于情况2：

当存在一个位置 \(I\) 选1时：
如图，此时 \(i\) 的两种选法中的每一次分别对应了 \(j\) 的两种选法，相互抵消了，所以不产生贡献
那当所有位置都选0时，因为此时 \(f(T)=a_i-1\)，就与 \(f(T')=a_i\) 产生了 \(1\) 的差值，产生了 \(-\mu\) 的贡献
然后就没有了

至于具体实现：我还是不会，巨丢人
最终在这里康懂了
每次筛到的一定是最小质因子
所以我们令这个数去掉这个最小质因子后等于 \(d\)
通过比较 \(d\) 的最小质因子的幂次以及 \(i\) 的最小质因子的幂次来看 \(h(i)\) 是否为0
需要特判几个情况

Code:

#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define N 10000010
#define ll long long
#define reg register int
//#define int long long 
#define max2(a, b) ((a)>(b)?(a):(b))

char buf[1<<21], *p1=buf, *p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf, 1, 1<<21, stdin)), p1==p2?EOF:*p1++)
inline int read() {
	int ans=0, f=1; char c=getchar();
	while (!isdigit(c)) {if (c=='-') f=-f; c=getchar();}
	while (isdigit(c)) {ans=(ans<<3)+(ans<<1)+(c^48); c=getchar();}
	return ans*f;
}

int n, m, T;
int pri[N], pcnt, h[N], a[N], b[N];
ll sumh[N];
bool npri[N];

signed main()
{
	for (reg i=2; i<N; ++i) {
		if (!npri[i]) pri[++pcnt]=i, h[i]=a[i]=1, b[i]=i;
		for (reg j=1,x,d; j<=pcnt&&i*pri[j]<N; ++j) {
			x=i*pri[j];
			npri[x]=1;
			if (!(i%pri[j])) {
				a[x]=a[i]+1;
				b[x]=b[i]*pri[j];
				d=i/b[i];
				if (d==1) h[x]=1;
				else h[x]=(a[i]+1==a[d])?-h[d]:0;
				break;
			}
			else h[x]=(a[i]==1)?-h[i]:0, a[x]=1, b[x]=pri[j];
		}
	}
	for (reg i=1; i<N; ++i) sumh[i]=sumh[i-1]+h[i];
	
	T=read();
	ll ans;
	while (T--) {
		n=read(); m=read(); ans=0;
		if (n>m) swap(n, m);
		for (reg l=1,r; l<=n; l=r+1) {
			r=min(n/(n/l), m/(m/l));
			ans+=1ll*(n/l)*(m/l)*(sumh[r]-sumh[l-1]);
		}
		printf("%lld\n", ans);
	}
	
	return 0;
}