题解 Lyk Love painting

传送门

30pts暴力冻傻了，碰都没碰

题意为将一个 \(2*n\) 的矩形划分成 \(m\) 个矩形，使得最大矩形的权值和最小
正解的话主要要维护一个性质
令 \(dp[i]\) 为上下同时填到位置 \(i\) 至少需要多少幅画
这样对于一个位置 \(i\)，我们只需要找最靠前的那个可以转移的决策点来进行转移
还有一种转移是下面这样

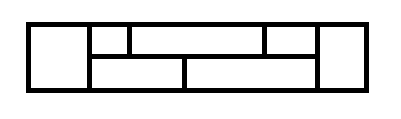
那么对于一个位置 \(i\)，我们不断向左填画进行转移
每次填两行里最短的那一个，取两者的max作为决策点，最多填不超过 \(m\) 幅画

所以总结是啥？DP通过转化为「至少」确保决策点单调？

Code:

#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define N 100010
#define ll long long
//#define int long long

char buf[1<<21], *p1=buf, *p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf, 1, 1<<21, stdin)), p1==p2?EOF:*p1++)
inline int read() {
	int ans=0, f=1; char c=getchar();
	while (!isdigit(c)) {if (c=='-') f=-f; c=getchar();}
	while (isdigit(c)) {ans=(ans<<3)+(ans<<1)+(c^48); c=getchar();}
	return ans*f;
}

int n, m;
int f[4][N];
ll mp[4][N], dp[N], sum[4][N], lim, maxn;

bool check(ll k) {
	//cout<<"check: "<<k<<endl;
	memset(f, 0, sizeof(f));
	memset(dp, 0x3f, sizeof(dp));
	dp[0]=0;
	for (int i=1; i<=3; ++i) 
		for (int j=1,l,r,mid; j<=n; ++j) {
			l=0, r=j;
			#if 1
			while (l<r) {
				mid=(l+r)>>1;
				//cout<<"mid: "<<j<<' '<<sum[3][j]<<' '<<sum[3][mid]<<endl;
				if (sum[i][j]-sum[i][mid]<=k) r=mid;
				else l=mid+1;
			}
			f[i][j]=l;
			#else
			for (int i=j; ~i; --i)
				if (sum[3][j]-sum[3][i]<=k) f[3][j]=i;
				else break;
			#endif
		}
	//cout<<"f3: "; for (int i=1; i<=n; ++i) cout<<f[3][i]<<' '; cout<<endl;
	#if 0
	for (int i=1,l,r,mid; i<=3; ++i)
		for (int j=0; j<=n; ++j) {
			l=j, r=n;
			#if 1
			while (l<=r) {
				mid=(l+r)>>1;
				if (sum[i][mid]-sum[i][j]<=k) l=mid+1;
				else r=mid-1;
			}
			f[i][j]=l-1;
			#else
			for (int h=j; h<=n; ++h)
				if (sum[i][h]-sum[i][j]<=k) f[i][j]=h;
				else break;
			#endif
		}
	#endif
	//cout<<"f1: "; for (int i=0; i<=n; ++i) cout<<f[1][i]<<' '; cout<<endl;
	//cout<<"f2: "; for (int i=0; i<=n; ++i) cout<<f[2][i]<<' '; cout<<endl;
	for (int i=0; i<=n; ++i) {
		dp[i]=min(dp[i], dp[f[3][i]]+1);
		for (int j=1,pos1=i,pos2=i; j<=m; ++j) {
			if (pos1>pos2) pos1=f[1][pos1];
			else pos2=f[2][pos2];
			//dp[min(pos1, pos2)]=min(dp[min(pos1, pos2)], dp[i]+j);
			dp[i]=min(dp[i], dp[max(pos1, pos2)]+j);
			//if (pos1==pos2) break;
		}
	}
	//cout<<"dp: "; for (int i=1; i<=n; ++i) cout<<dp[i]<<' '; cout<<endl;
	//cout<<"return: "<<dp[n]<<' '<<(dp[n]<=m)<<endl;
	return dp[n]<=m;
}

signed main()
{
	n=read(); m=read();
	for (int i=1; i<=n; ++i) mp[1][i]=read(), mp[3][i]+=mp[1][i], lim+=mp[1][i], maxn=max(maxn, mp[1][i]);
	for (int i=1; i<=n; ++i) mp[2][i]=read(), mp[3][i]+=mp[2][i], lim+=mp[2][i], maxn=max(maxn, mp[2][i]);
	for (int i=1; i<=n; ++i) {
		sum[1][i]=sum[1][i-1]+mp[1][i];
		sum[2][i]=sum[2][i-1]+mp[2][i];
		sum[3][i]=sum[3][i-1]+mp[3][i];
	}
	//cout<<"sum3: "; for (int i=1; i<=n; ++i) cout<<sum[3][i]<<' '; cout<<endl;
	ll l=maxn, r=lim+1, mid;
	while (l<r) {
		mid=(l+r)>>1;
		if (check(mid)) r=mid;
		else l=mid+1;
	}
	printf("%lld\n", l);
	//for (int i=1; i<=lim; ++i)
	//	if (check(i)) {cout<<i<<endl; break;}

	return 0;
}