题解 Miner
题面劝退+冻的要死
看着subtask5 puts("0"); 白送的分愣是没起来打……
- 看到无向图中形如「可以传送到任意点」的条件,实际上就是在说可以任意加边
- 看到形如「每条边经过且仅经过一次」的限制首先考虑欧拉路,别先想别的各类复杂图
首先不考虑加边什么的,问题就是在求欧拉路
现在还要给它加边,考虑要加的边有什么特点
让加的边数尽量少的话,应该是尽量把入度为奇的点都连起来,再把连通块都连起来,使入度为奇的点只有两个
那就分连通块考虑,令连通块 \(i\) 中入度为奇的点个数为 \(c_i\)
那么应加边数为
\[\frac{\sum\limits_{c_i>0} c_i}{2}-1+\sum[c_i=0]
\]
也即
\[\sum max(\frac{c_i}{2}, 1)
\]
那么考虑构造方案
其实就是加边使原图成为欧拉图,然后找出一条欧拉路就行了
至于这个过程如何实现
先在奇度数点之间加边,使原图中没有奇度数点,特殊标记新加的边
然后对每个连通块求欧拉路,新加的边会将路径分为几个部分,我们称为「一段路径」
那么路径之间是可以任意组合的,求出所有路径之后用1边串起来就行了
然后发现dfs会爆栈,需要手动模拟实现
- 一遍dfs求欧拉路
md劳资居然不会真丢人
从一个奇度数点出发,不断挑选一条未标记过的边dfs下去,在回溯时将这个点入栈,最后倒序输出栈
这实际上确保了与这个点相连的所有边都被经过了
感性理解一下,入边被强制最后入栈了
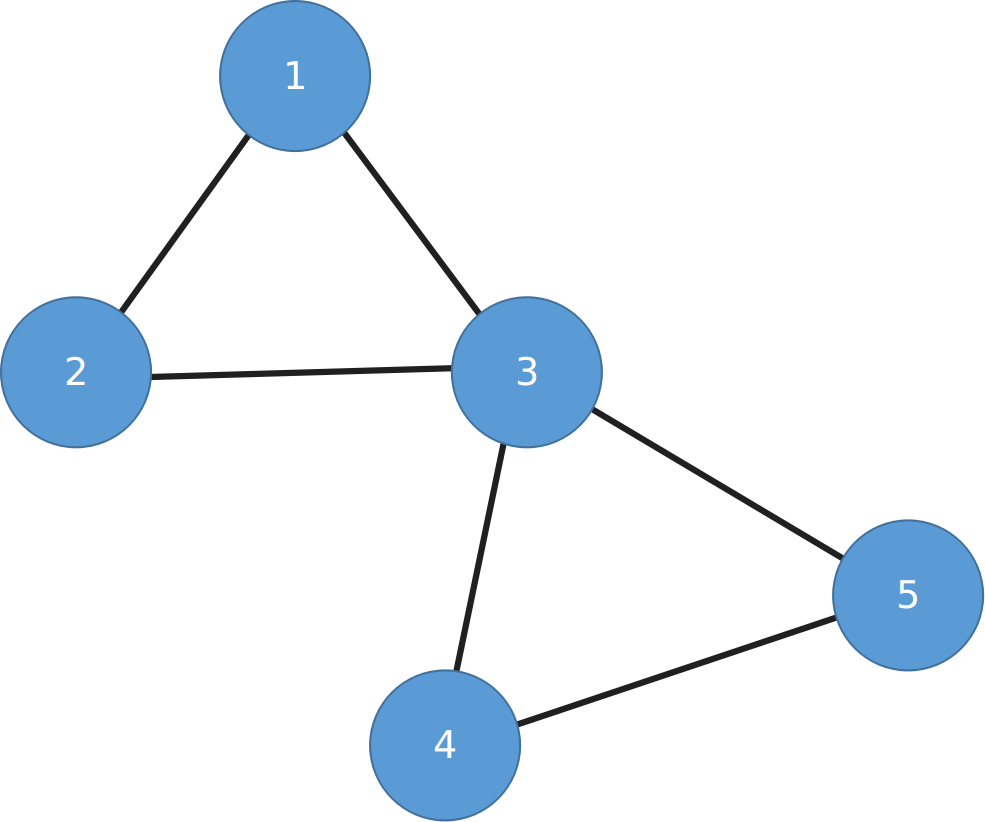
这里dfs到3的时候两种可能
如果去2,则在栈中3的子树在2和3之间,被考虑到了
如果去4/5,则从子树中一路dfs下去可以遍历到2,也是合法的
Code:
#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define N 100010
#define ll long long
#define pb push_back
#define fir first
#define sec second
#define make make_pair
//#define int long long
char buf[1<<21], *p1=buf, *p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf, 1, 1<<21, stdin)), p1==p2?EOF:*p1++)
inline int read() {
int ans=0, f=1; char c=getchar();
while (!isdigit(c)) {if (c=='-') f=-f; c=getchar();}
while (isdigit(c)) {ans=(ans<<3)+(ans<<1)+(c^48); c=getchar();}
return ans*f;
}
int n, m;
int head[N], size=1, cnt[N], fa[N], c[N], sta[N<<1], top, s, tot, odd[N], osiz, now;
bool vis[N<<2], vis2[N];
pair<int, int> sta2[N<<1];
struct edge{int to, next; bool ext;}e[N<<2];
struct ring{vector< pair<int, int> > v;}r[N<<1];
struct path{vector<int> v;}p[N<<1];
inline void add(int s, int t) {e[++size].to=t; e[size].ext=0; e[size].next=head[s]; head[s]=size;}
inline void add(int s, int t, bool typ) {e[++size].to=t; e[size].ext=typ; e[size].next=head[s]; head[s]=size;}
inline int find(int p) {return fa[p]==p?p:fa[p]=find(fa[p]);}
signed main()
{
memset(head, -1, sizeof(head));
n=read(); m=read();
for (int i=1; i<=n; ++i) fa[i]=i;
for (int i=1,u,v; i<=m; ++i) {
u=read(); v=read();
add(u, v); add(v, u);
++cnt[u]; ++cnt[v];
fa[find(u)]=find(v);
}
for (int i=1,f; i<=n; ++i) if (cnt[i]) {
f=find(i);
if (!vis[f]) sta[++top]=f, vis[f]=1;
if (cnt[i]&1) ++c[f], odd[++osiz]=i;
}
ll ans=0;
while (top) ans+=max(c[sta[top--]]/2, 1); //, cout<<c[sta[top+1]]<<endl;
printf("%lld\n", ans-1);
memset(vis, 0, sizeof(bool)*(n+5));
for (int i=2; i<=osiz; i+=2) add(odd[i-1], odd[i], 1), add(odd[i], odd[i-1], 1), fa[find(odd[i-1])]=find(odd[i]);
for (int i=1; i<=n; ++i) if (cnt[i] && !vis2[find(i)]) {
sta2[++top]=make(i, 0); vis2[find(i)]=1; ++now;
while (top) {
pair<int, int> u=sta2[top];
for (int i=head[u.fir]; ~i; head[u.fir]=i=e[i].next) if (!vis[i]) {
//cout<<"ext: "<<e[i].ext<<endl;
sta2[++top]=make(e[i].to, e[i].ext);
vis[i]=vis[i^1]=1;
head[u.fir]=e[i].next;
goto jump;
}
--top;
r[now].v.pb(u);
jump: ;
}
//r[now].v.pb(make(i, 0));
reverse(r[now].v.begin(), r[now].v.end());
}
//cout<<"now: "<<now<<endl;
for (int i=1,lst=0; i<=now; ++i) {
int pos1=0, pos2=0, beg=0;
//cout<<"rsiz: "<<r[i].v.size()<<endl;
//for (auto it:r[i].v) cout<<it.fir<<','<<it.sec<<' '; cout<<endl;
while (pos1<r[i].v.size() && !r[i].v[pos1].sec) ++pos1;
//cout<<"then pos1: "<<pos1<<endl;
if (pos1>=r[i].v.size()) {
++tot;
for (auto it:r[i].v) p[tot].v.pb(it.fir);
}
else {
beg=pos1;
for (pos2=pos1+1; pos2<r[i].v.size(); pos1=pos2,++pos2) {
while (pos2<r[i].v.size() && !r[i].v[pos2].sec) ++pos2;
//cout<<"then pos2: "<<pos2<<endl;
++tot;
for (int j=pos1; j<pos2; ++j) p[tot].v.pb(r[i].v[j].fir); //, cout<<"pb: "<<r[i].v[j].fir<<endl;
}
for (int j=1; j<beg; ++j) p[tot].v.pb(r[i].v[j].fir); //, cout<<"pb2: "<<r[i].v[j].fir<<endl;
}
}
//cout<<"tot: "<<tot<<endl;
for (int i=1,lst=0; i<=tot; ++i) {
if (!lst) printf("%d\n", p[i].v[0]);
else printf("1 %d\n", p[i].v[0]);
lst=p[i].v[0];
for (int j=1; j<p[i].v.size(); ++j) printf("0 %d\n", p[i].v[j]);
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号