OI选手常见作死错误列表
哦对这个题目是抄来的
1.关于动态内存
貌似noip测评时算的是静态内存?也就是说,申请的内存释不释放好像并没有什么区别…… 而且加上delete之后有几率触发随机玄学错误特效还是不加的好
2021.4.23 upd: noip测评时算的的确是静态内存,只要申请过就会计入总内存,delete完全没有用。小心考场上因为这个爆内存。
delete释放:
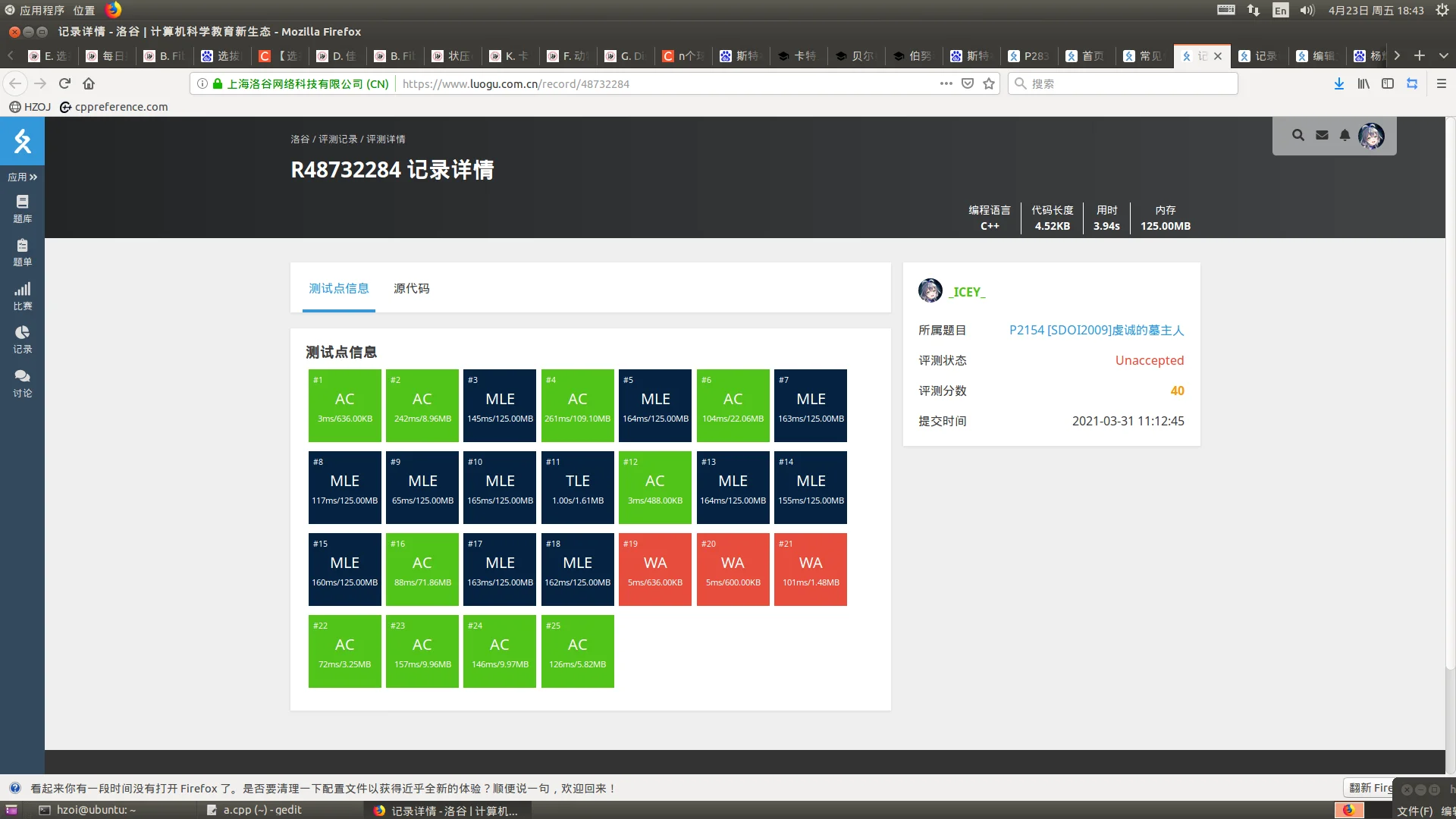
不释放:
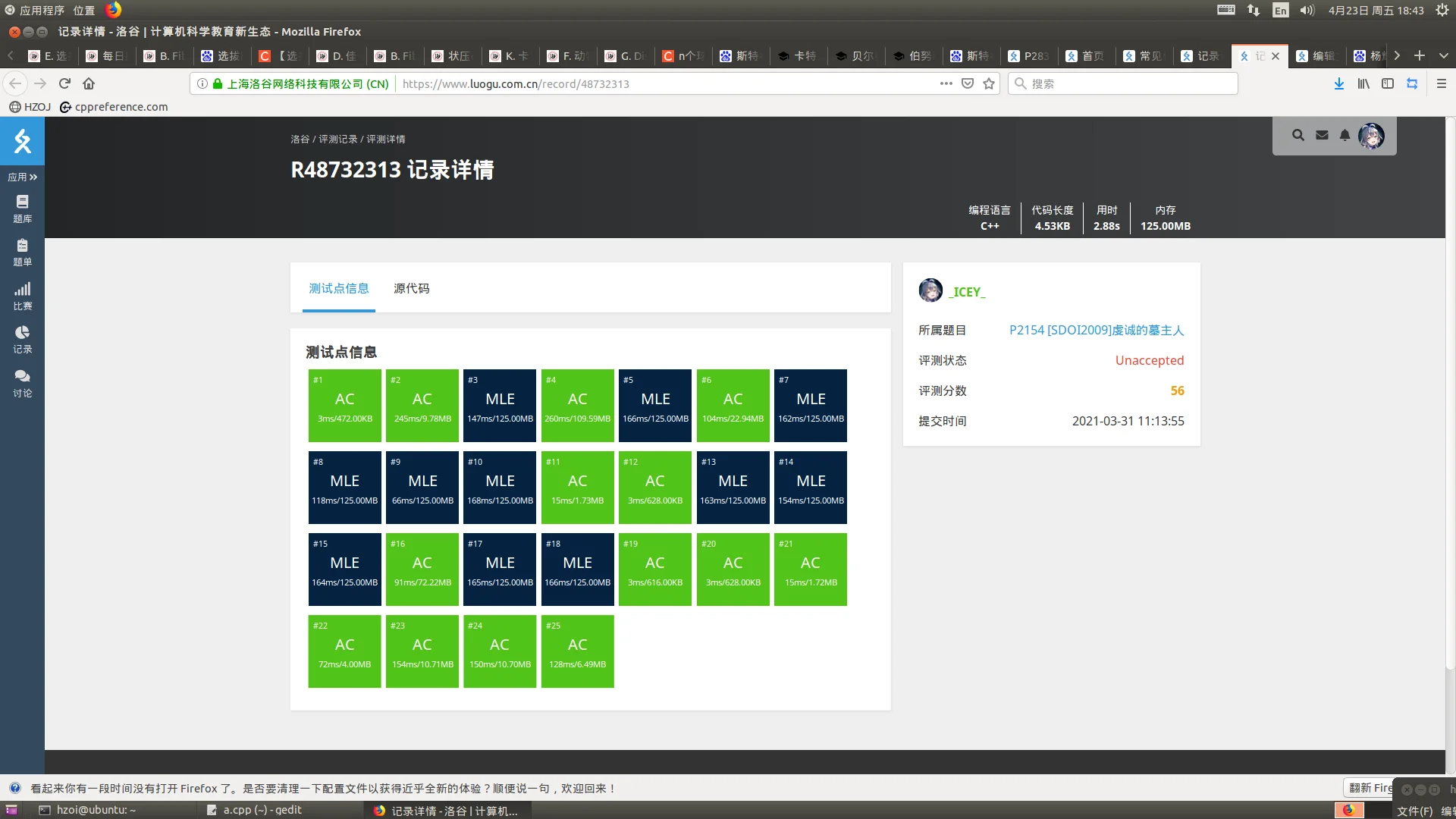
2.关于运算优先级
!(i&1<<c) 和 !i&1<<c 并不等价
(s|per[j]==s) 和 (s|per[j])==s 并不等价
==的优先级比&,|高,所以是s|(1<<i)==s实际上会被理解为s|((1<<i)==s)
3.状压DP
首先注意第2点。
还有 某些状压DP的题状态s不从0开始枚举就是找死
4.关于bitset卡常
(并不知道对不对)由于处理器特性,在某些机器上bitset修改/连续访问/随机访问貌似需要一次取出8位,导致其速度尽失。所以开bitset反而可能T飞。
p.s. 具体来说,bitset源码中有大量#if __cplusplus >= 201103L形式的优化,而这些优化在g++ 4.8.4上是不起作用的,即使开了c++11也没用,所以考场上不建议使用。另外,经笔者实测(使用g++ 8.2.0),在高版本编译器上bitset就会快许多了。
5.关于四舍五入
printf四舍五入有舍入误差,输出时记得加上个eps
具体原理详见这篇文章
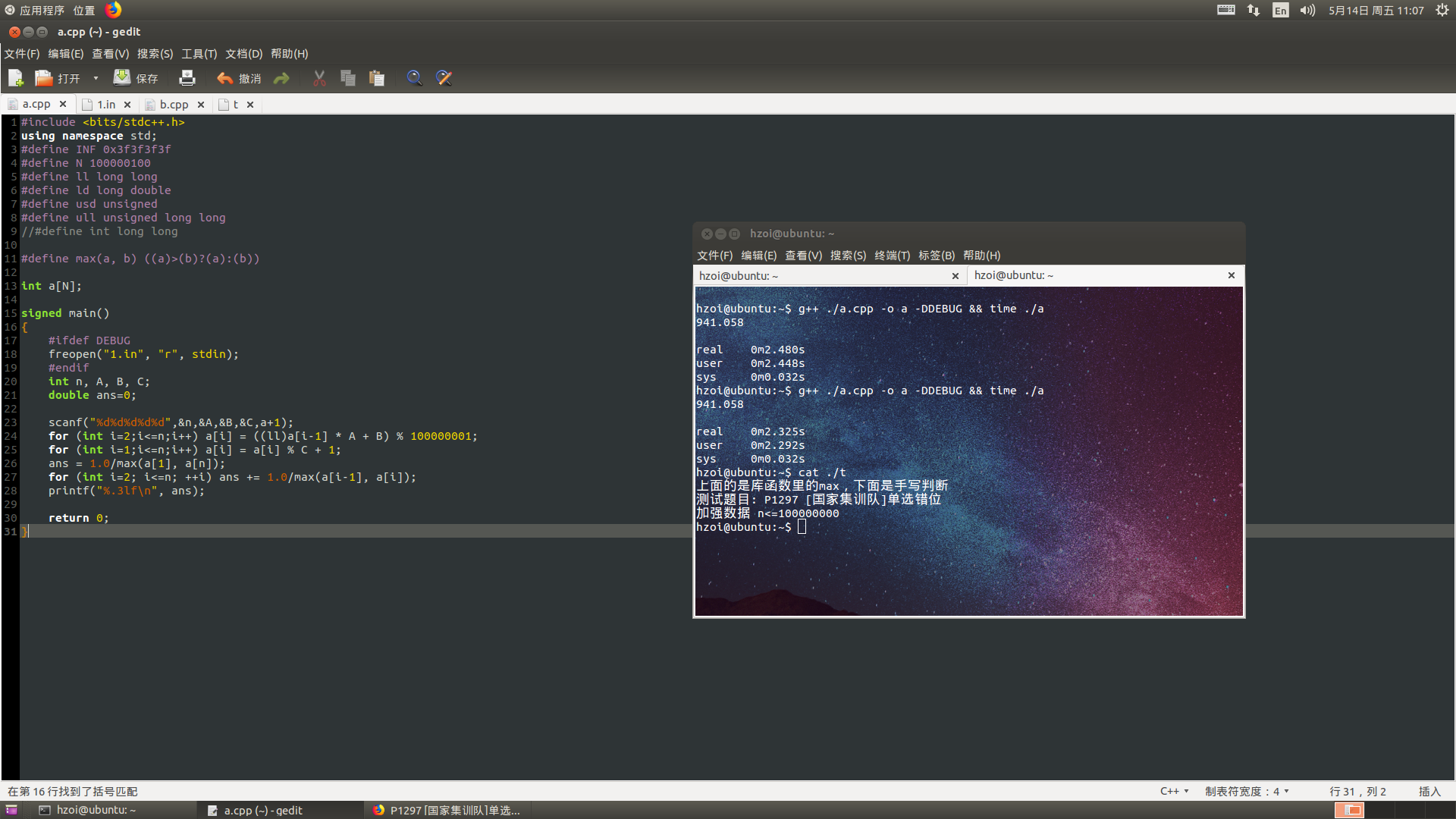
6.关于max
手写max真的快过库函数中的max函数。
7.关于INF
对于long long, 0x3f3f3f3f真的不算大。如果有明显需要开long long的题, 记得调一下INF。
反正都开long long了, INF就往大了开就好了, 可以考虑一下0x7ffffffffff
8.关于二分答案
如果二分区间是[l, r], 那个r其实是取不到的, 需要视情况+1
有需要根据数据确定二分上界的题(比如这道[NOIP2011 提高组] 聪明的质监员), r不+1的话可能被卡虽然官方数据没卡
#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define N 100010
#define ll long long
#define ld long double
#define usd unsigned
#define ull unsigned long long
//#define int long long
inline int read() {
int ans=0, f=1; char c=getchar();
while (!isdigit(c)) {if (c=='-') f=-f; c=getchar();}
while (isdigit(c)) {ans=(ans<<3)+(ans<<1)+(c^48); c=getchar();}
return ans*f;
}
struct trie{
int son[2], cnt[2], val;
#define t(p) tree[p]
}tree[N*31];
int n, size;
int add(int dat) {
int p=0, t;
int t2;
for (int i=30; i>=0; --i) {
t2 = (dat&(1<<i))?1:0;
//cout<<i<<' '<<t2<<endl;
t=t(p).son[t2]; ++t(p).cnt[t2];
if (!t) {t(p).son[t2]=++size; t=size; t(t).val=t2;}
p = t;
}
return 3;
}
int query(int u, int p1, int p2) {
//cout<<"query "<<u<<' '<<p1<<' '<<p2<<endl;
if (u<0) return 0;
int ans=0; bool vis=0;
int s10=t(p1).son[0], s11=t(p1).son[1], s20=t(p2).son[0], s21=t(p2).son[1];
//if (u==4 || u==5) {cout<<s10<<' '<<s11<<' '<<s20<<' '<<s21<<endl; cout<<p1<<' '<<p2<<endl; cout<<t(p1).val<<' '<<t(p2).val<<endl;}
if (s11&&s20) {ans=max(ans, query(u-1, s11, s20)|(1<<u)); vis=1;}
if (s10&&s21) {ans=max(ans, query(u-1, s10, s21)|(1<<u)); vis=1;} 这个地方,如果|(1<<u)写在外面会炸锅
if (!vis && p1==p2) {
if (t(p1).cnt[0]>1) ans=max(ans, query(u-1, s10, s10));
if (t(p1).cnt[1]>1) ans=max(ans, query(u-1, s11, s11));
}
else if (!vis && p1!=p2) {
if (s11&&s21) ans=max(ans, query(u-1, s11, s21));
if (s10&&s20) ans=max(ans, query(u-1, s10, s20));
}
//cout<<"return "<<u<<' '<<ans<<endl;
return ans;
}
signed main()
{
#ifdef DEBUG
freopen("1.in", "r", stdin);
#endif
n=read();
for (int i=1; i<=n; ++i) add(read());
printf("%d\n", query(30, 0, 0));
return 0;
}
8.一些细节问题:
-
整数解高斯消元要注意doubel转int的时候可能被卡精度
-
开fread了就别再用scanf之类了, 发现程序没读入可能是fread的锅
-
参数表里的参数处理顺序貌似是随机的,所以形如
upd(read(), 1, n, read())这样的写法可能会炸 -
建边写成edge e; e=new edge[m2+10]是正优化
-
lca预处理lg数组(貌似)是正优化,预处理bin数组是负优化
-
写完hash要写--n!
-
inline int md(int& a, int t) {a+=t; a=(a>=mod?a-mod:(a<=-mod?a+mod:a));}是负优化,还没有%mod快 -
动态开点线段树写垃圾回收机制要记得写废点的clear操作(或者在每次开新点的时候清空一下)
-
要求取最大值的题目,注意这个最大值能不能是负的
-
cnt(p)=cnt(p<<1)+cnt(p<<1|1)-(rcol(p<<1)==lcol(p<<1|1));
和
cnt(p)=cnt(p<<1)+cnt(p<<1|1)-rcol(p<<1)==lcol(p<<1|1);
并不是等价写法,巨坑
-
当输入形似 Q 3 5 ,即最前面会有一个字符时,不能偷懒定义一个char c,然后scanf("%s%d%d", &c, &a, &b);
因为c风格字符串结尾处会有一个'\0',这个'\0'在这里会越界。必须定义一个长度\(\geqslant 2\)的字符数组 -
kruskal重构树:别忘了这个东西,这里讲的还行,建议BFS下它的性质,还有重新连边的时候别忘了处理虚点
-
开O2线段树数组实现比结构体实现快一些,但不开O2数组实现略慢
-
对于像火星人这样字符串的长度在不断增大的字符串hash,p[]数组要预处理够,否则字符串长度增加之后hash可能会炸掉
-
一个数的质因数大约有log个
-
线段覆盖问题,要求坐标 \(i\) 不能被超过 \(a_i\) 条线段覆盖,很常见的模板题
-
序列问题出现形如「区间间只有包含和不相交关系」的限制条件时,把它扔树上去
-
序列的左右区间/树上的左右子树相乘,可以转化为两个区间/子树内的点对个数(?)
-
对于一个序列,两两异或和最小值就是排完序后相邻元素异或和的最小值,也即若 \(a<b<c\),有 \(a \oplus c \geqslant min\{a \oplus b, b \oplus c\}\)
-
树上子树以权值线段树形式向上合并且每次合并需要整体平移1,考虑转化,令t为时刻,d为深度,则其下标可以表示为 \(t+\Delta t+d\),而 \(d=\Delta t\),所以可以消掉
-
开题三问:它有单调性吗?某种合法数的个数/可行操作数是log/根号的吗?
-
AC自动机上如果要求某个串不能出现,那所有包含这个串的串都不能出现
也即如果 \(fail_x\) 非法,那 \(x\) 也是非法的(这个容易忘了处理) -
dfs判环:一直写不对太丢人了
bool dfs(int u) { vis[u]=ring[u]=1; for (int i=head[u],v; ~i; i=e[i].next) { v = e[i].to; if (ring[v]) return 1; if (!vis[v] && dfs(v)) return 1; } ring[u]=0; } -
「是一个串的子串」即「是一个串前缀的后缀」
-
取模的题输出的时候要再取一遍模!尤其是模数由输入给定的时候,某些沙雕数据可能让你对1取模
-
AC自动机上跑状压注意建图的时候把后缀信息也或进去
-
稀疏矩阵消元在类似这样的题里有用,
但我还不会 -
在一张图上随机游走,每个点的期望经过次数就等于每个时刻在这个点的概率之和
这个配合矩阵快速幂会很好用,见这题 -
分块可以处理形如链/DAG上带修前缀和问题,比如这个
-
错位排列:\(D_n = (n-1)*(D_{n-2}+D_{n-1})\)
-
\(σ0\) 和 \(\varphi\) 在素数幂处的值很容易得到: \(k>0\) 时 \(\sigma_0(p^k)=k+1\),\(\varphi(p^k)=p^{k-1}(p-1)\)
-
\(\sum\limits_{i=1}^n k\bmod i = \sum\limits_{i=1}^n k-i\lfloor \frac{k}{i} \rfloor\)

 浙公网安备 33010602011771号
浙公网安备 33010602011771号