题解 单
本来当本场保分题做的,结果爆零了,自闭ing
首先t=0的情况就是个双爆搜的板子,然而我下推的dfs式子推错了
下推部分出错时靠近根节点的节点不一定会错,所以一定要完整地手模几组样例!
b数组考场上推了半天式子没找到思路,最后打了个高斯消元走人,结果被卡精度了
整数解高斯消元要注意doubel转int的时候可能被卡精度,建议加个0.5再强制转换
好了下面是题解:
对于t=1的情况,以1节点为根,令\(sum[i]\)为每个点的子树(包括自身)的权值和,则\(sum[1]\)为总权值和,联想前缀和,整棵树上除i的子树以外的节点的权值和就是\(sum[1]-sum[i]\)。
看到b数组的定义,不难猜到, 某两个点的b值相减应该能消掉大部分项。每个\(a[i]\)的系数是\(dis(i, v)\) 这个系数在相邻的节点上总是差一,所以考虑让两个相邻节点相减
这里有个问题:在一棵树上,\(sum[]\)数组的处理是基于子树的,也就是说两个相邻节点必有一个是另一个的子节点。令两节点分别为i, fa, 这里拿点1和点2举个例子:
图是盗来的
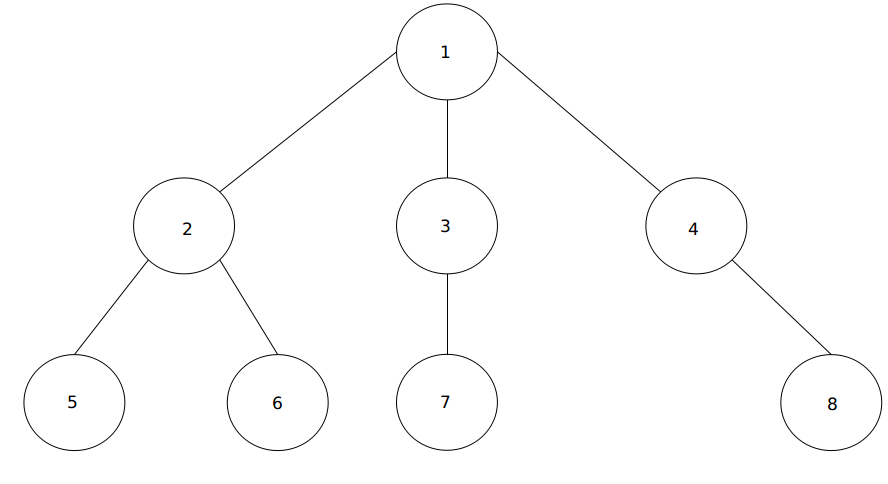
这里 也是盗来的
\(b[1]=a[1]*0+a[2]*1+a[3]*1+a[4]*1+a[5]*2+a[6]*2+a[7]*2+a[8]*2\)
\(b[2]=a[1]*1+a[2]*0+a[3]*2+a[4]*2+a[5]*1+a[6]*1+a[7]*3+a[8]*3\)
从图中我们可以发现,两式相减后所有a[i]的系数绝对值为1. 再考虑正负,发现两节点中子节点子树系数均为负.
联想前缀和,我们可以表示出\(b[i]-b[fa]=sum[i]-(sum[1]-sum[fa])=sum[1]-2*sum[i]\)
尝试消去式中所有sum[i], 令\(tot = \sum_{i!=1}b[i]-b[fa] = (n-1)sum[1]-2\times\sum_{i!=1}sum[i]\)
这里\(\sum_{i!=1}sum[i] = b[1]\),所以原式可化为\(\sum_{i!=1}b[i]-b[fa] = (n-1)sum[1]-2*b[1]\)
b数组已知,则可解出\(sum[1]\),利用\(b[i]-b[fa]=sum[i]-(sum[1]-sum[fa])=sum[1]-2*sum[i]\), 可用一遍dfs解出所有\(sum[i]\).
再根据\(sum[leaf] = a[leaf]\), 再跑一遍dfs回溯可解出所有\(a[i]\).
Code:
#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define N 100010
#define ll long long
#define ld long double
#define usd unsigned
#define ull unsigned long long
//#define int long long
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf, 1, 1<<21, stdin)), p1==p2?EOF:*p1++)
char buf[1<<21], *p1=buf, *p2=buf;
inline int read() {
int ans=0, f=1; char c=getchar();
while (!isdigit(c)) {if (c=='-') f=-f; c=getchar();}
while (isdigit(c)) {ans=(ans<<3)+(ans<<1)+(c^48); c=getchar();}
return ans*f;
}
struct matrix{
int n, m;
static const int SIZE=1010;
double* a[SIZE];
void newarr() {for (int i=1; i<SIZE; ++i) {a[i]=new double[SIZE]; memset(a[i], 0, sizeof(double)*SIZE);}}
matrix(){newarr();}
void resize(int k, int g) {n=k; m=g;}
void clear() {for (int i=1; i<SIZE; ++i) memset(a[i], 0, sizeof(double)*SIZE);}
void put() {for (int i=1; i<=n; ++i) {for (int j=1; j<=m; ++j) cout<<a[i][j]<<' '; cout<<endl;}}
inline void change(int i, int j) {swap(a[i], a[j]);}
inline double* operator [] (int i) {return a[i];}
void gauss(int* ans) {
for (int i=1; i<=n; ++i) {
int r=i;
for (int j=i+1; j<=n; ++j) if (a[j][i]>a[i][i]) r=j;
change(i, r);
for (int j=1; j<=n; ++j) {
if (i==j || !a[j][i] || !a[i][i]) continue;
double t1=a[j][i], t2=a[i][i];
//cout<<t1<<' '<<t2<<endl;
for (int k=i; k<=m; ++k) a[j][k] -= a[i][k]*t1/t2;
}
//put(); cout<<endl;
}
for (int i=1; i<=n; ++i) ans[i] = int(a[i][m]/a[i][i]+0.5);
}
}mat;
struct edge{int to, next;}e[N<<1];
int n;
int head[N], size, a[N], root;
int dp[N], cnt[N], dis[N];
ll sum[N], b[N], tot;
inline void add(int s, int t) {edge* k=&e[++size]; k->to=t; k->next=head[s]; head[s]=size;}
void dfs1(int u, int in_edge) {
//cout<<"dfs1 "<<u<<endl;
in_edge ^= 1;
if (cnt[u]==1 && u!=1) return ;
for (int i=head[u],v; i; i=e[i].next) {
v = e[i].to;
if (i==in_edge) continue;
dfs1(v, i);
sum[u] += sum[v]+a[v];
dp[u] += dp[v];
}
dp[u] += sum[u];
}
void dfs2(int u, int in_edge, int dat, int sumf) {
//cout<<"dfs2 "<<u<<' '<<dat<<' '<<sumf<<endl;
in_edge ^= 1;
b[u] = dp[u]+dat;
for (int i=head[u],v; i; i=e[i].next) {
v = e[i].to;
if (i!=in_edge) dfs2(v, i, dat+sumf+dp[u]-dp[v]-2*a[v]-2*sum[v]+sum[u]+a[u], sumf+sum[u]+a[u]-sum[v]-a[v]);
}
}
void dfs3(int u, int in_edge, int dat) {
in_edge ^= 1;
dis[u] = dat;
if (cnt[u]==1 && u!=root) return ;
for (int i=head[u],v; i; i=e[i].next) {
v = e[i].to;
if (i!=in_edge) dfs3(v, i, dis[u]+1);
}
}
void dfs4(int u, int in_edge, int fa) {
in_edge ^= 1;
tot += b[u]-b[fa];
if (cnt[u]==1 && u!=1) return ;
for (int i=head[u],v; i; i=e[i].next) {
v = e[i].to;
if (i!=in_edge) dfs4(v, i, u);
}
}
void dfs5(int u, int in_edge, int fa) {
in_edge ^= 1;
sum[u] = (sum[1]+b[fa]-b[u])/2;
a[u] = sum[u];
if (cnt[u]==1 && u!=1) return ;
for (int i=head[u],v; i; i=e[i].next) {
v = e[i].to;
if (i!=in_edge) {dfs5(v, i, u); a[u]-=sum[v];}
}
}
signed main()
{
#ifdef DEBUG
freopen("1.in", "r", stdin);
#endif
int k, t;
k=read();
while (k--) {
size=1; tot=0;
memset(head, 0, sizeof(head));
memset(dp, 0, sizeof(dp));
memset(sum, 0, sizeof(sum));
memset(cnt, 0, sizeof(cnt));
n=read();
for (int i=1,u,v; i<n; ++i) {u=read(); v=read(); add(u, v); add(v, u); ++cnt[u]; ++cnt[v];}
t=read();
if (!t) {
for (int i=1; i<=n; ++i) a[i]=read();
dfs1(1, 0);
b[1] = dp[1];
dfs2(1, 0, 0, 0);
for (int i=1; i<=n; ++i) printf("%lld ", b[i]); printf("\n");
//cout<<"dp "; for (int i=1; i<=n; ++i) cout<<dp[i]<<' '; cout<<endl;
//cout<<"sum "; for (int i=1; i<=n; ++i) cout<<sum[i]<<' '; cout<<endl;
//cout<<"a[i] "; for (int i=1; i<=n; ++i) cout<<a[i]<<' '; cout<<endl;
}
else {
#if 0
mat.clear();
mat.resize(n, n+1);
for (int i=1; i<=n; ++i) b[i]=read();
for (int i=1; i<=n; ++i) {
dis[i]=0; root=i;
dfs3(i, 0, 0);
//cout<<"dis "; for (int i=1; i<=n; ++i) cout<<dis[i]<<' '; cout<<endl;
for (int j=1; j<=n; ++j) mat[i][j]=dis[j];
mat[i][i]=0;
mat[i][n+1] = b[i];
}
//mat.put(); cout<<endl;
mat.gauss(a);
for (int i=1; i<=n; ++i) printf("%d ", a[i]); printf("\n");
#else
for (int i=1; i<=n; ++i) b[i]=read();
for (int i=head[1],v; i; i=e[i].next) {
v = e[i].to;
dfs4(v, i, 1);
}
sum[1] = (tot+2*b[1])/(n-1);
a[1] = sum[1];
for (int i=head[1],v; i; i=e[i].next) {
v = e[i].to;
dfs5(v, i, 1);
a[1] -= sum[v];
}
for (int i=1; i<=n; ++i) printf("%d ", a[i]); printf("\n");
//cout<<"sum "; for (int i=1; i<=n; ++i) cout<<sum[i]<<' '; cout<<endl;
#endif
}
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号