PRML读书笔记_绪论
一、基本名词##
泛化(generalization)###
训练集所训练的模型对新数据的适用程度。
监督学习(supervised learning)###
训练数据的样本包含输入向量以及对应的目标向量。
- 分类( classification ):给每个输入向量分配到有限数量离散标签中的一个。
- 回归( regression ):输出由一个或者多个连续变量组成。
无监督学习(unsupervised learning)###
训练数据由一组输入向量 x 组成,没有任何对应的目标值。
- 聚类(clustering):发现数据中相似样本的分组。
- 密度估计(density estimation):决定输入空间中数据的分布。
反馈学习(reinforcement learning)###
在给定的条件下,找到合适的动作,使得奖励达到最大值。学习问题没有给定最优输出的用例。这些用例必须在一系列的实验和错误中被发现。
反馈学习的一个通用的特征是探索( exploration )和利用( exploitation )的折中,过分地集中于探索或者利用都会产生较差的结果。
- 探索:是指系统尝试新类型的动作,
- 利用:是指系统使用已知能产生较高奖励的动作。
二、概率论##
1.概率论的两个基本规则:加和规则( sumrule )、乘积规则( product rule )###
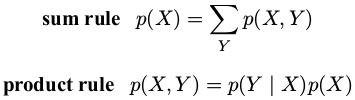
2.贝叶斯定理( Bayes' theorem )###
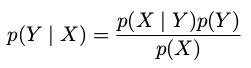
贝叶斯定理中的分母可以用出现在分子中的项表示:
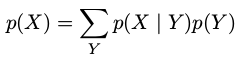
- 先验概率( prior probability ):\(p(Y)\) 在未知\(X\)分布时,我们已知\(Y\)分布,顾称\(p(Y)\)为先验。
- 后验概率( posterior probability ):\(p(Y|X)\) 在得知\(X\)分布后,加入\(p(X)\)的约束可以的到条件概率\(p(Y|X)\),称之为后验。
3.概率密度###
概率密度( probability density )####
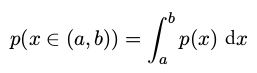
满足下面两个条件:

一个变量的变化\(x = g(y)\) , 那么函数\(f (x)\)就变成了$ f ̃ (y) = f (g(y))$
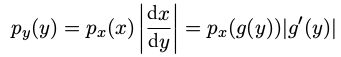
累积分布函数( cumulative distribution function )####
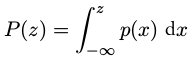
概率密度函数加和规则和乘积规则####
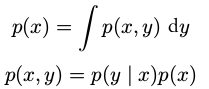
4.期望和协方差###
期望( expectation )####
离散变量
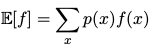
连续变量
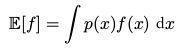
方差( variance )####
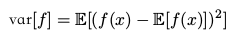
可以化为:
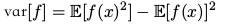
协方差( covariance )####
协方差是对两个随机变量 x 和 y而言:

在两个随机向量 x 和 y 的情形下,协方差是一个矩阵:
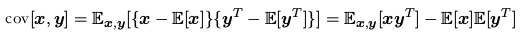



 浙公网安备 33010602011771号
浙公网安备 33010602011771号