OpenGL坐标转换

转自

1. OpenGL 渲染管线##

让我们先来弄清楚OpenGL中的渲染管线。管线是一个抽象的概念，之所以称之为管线是因为显卡在处理数据的时候是按照一个固定的顺序来的，而且严格按照这个顺序。就像水从一根管子的一端流到另一端，这个顺序是不能打破的。先来看看下面的图1：

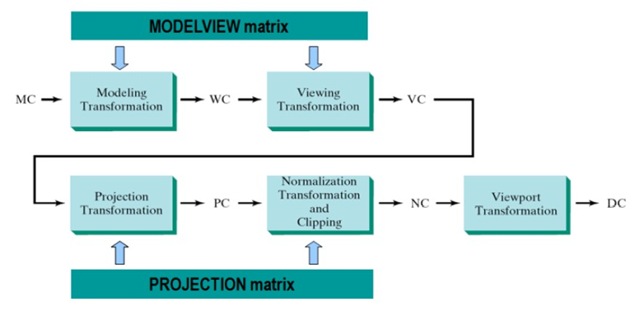
图中显示了OpenGL图形管线的主要部分，也是我们在进行图形编程的时候常常要用到的部分。一个顶点数据从图的左上角(MC)进入管线，最后从图的右下角(DC)输出。
MC是Model Coordinate的简写，表示模型坐标，也说成本地坐标(相对于世界坐标)，该坐标系与模型固联。
DC是Device Coordinate的简写，表示设备坐标。当然DC有很多了，什么显示器，打印机等等。这里DC我们就理解成常说的屏幕坐标好了。

1.1模型观测变换(ModelView Transformation)###

MC要经过模型变换(Modeling Transformation)才变换到世界坐标WC，说简单点就是如何用世界坐标系来表示本地坐标系中的坐标。为了讲得更清楚一些，这里举个2D的例子。如图2：

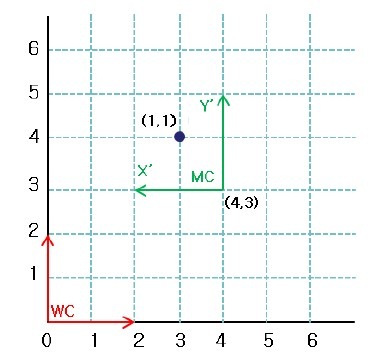
图中红色坐标系是世界坐标系WC，绿色的是模型坐标系MC。现在有一个顶点，在模型坐标系中的坐标为(1,1)，现在要把这个模型坐标转换到世界坐标中来表示。从图中可以看出，点(1,1)在世界坐标系中的坐标为(3,4)，现在我们来通过计算得到我们希望的结果。首先我们要把模型坐标系MC在世界坐标系中表示出来，使用齐次坐标(Homogeneous Coordinate )可以表示为矩阵(注意，本教程中使用的矩阵都是以列向量组成)：

\[ MC = \left[ \begin{array}{ccc} -1 & 0 & 4 \\ 0 & 1 & 3 \\ 0 & 0 & 1 \end{array} \right] \]

其中，矩阵的第一列为MC中x轴在WC中的向量表示，第二列为MC中y轴WC中的向量表示，第三列为MC中的原点在WC中的坐标。有了这个模型变换矩阵后，用这个矩阵乘以在MC中表示的坐标就可以得到该坐标在世界坐标系中的坐标。所以该矩阵和MC中的坐标(1,1)相乘有:

\[ \left[ \begin{array}{ccc} -1 & 0 & 4 \\ 0 & 1 & 3 \\ 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] = \left[ \begin{array}{c} 3 \\ 4 \\ 1 \end{array} \right] \]

这也正是我们需要的结果。现在让我们把相机坐标也加进去，相机坐标也称为观测坐标(View Coordinate)，如图3:

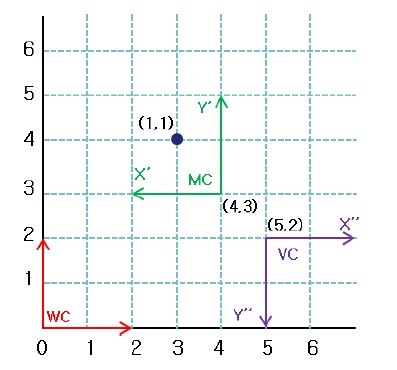
来看看MC坐标中的点(1,1)如何在相机坐标中表示。从图5中可以直接看出MC中的点(1,1)在相机坐标系VC中为(-2,-2)。和上面同样的道理，我们可以写出相机坐标系VC在世界标系WC中可以表示为：

\[ VC = \left[ \begin{array}{ccc} 1 & 0 & 5 \\ 0 & -1 & 2 \\ 0 & 0 & 1 \end{array} \right] \]

那么世界坐标系中的点转换为相机坐标系中的点我们就需求VC的逆矩阵：

\[ VC^{-1} = \left[ \begin{array}{ccc} 1 & 0 & -5 \\ 0 & -1 & 2 \\ 0 & 0 & 1 \end{array} \right] \]

那么世界坐标系WC中的点(3,4)在相机坐标系VC中坐标为：

\[ \left[ \begin{array}{ccc} 1 & 0 & -5 \\ 0 & -1 & 2 \\ 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} 3 \\ 4 \\ 1 \end{array} \right] = \left[ \begin{array}{c} -2 \\ -2 \\ 1 \end{array} \right] \]

上面的变换过程，就是可以把模型坐标变换为相机坐标。在OpenGL中，当我们申明顶点的时候，有时候说的是世界坐标，这是因为初始化的时候世界坐标系、模型坐标系和相机坐标系是一样的，重合在一起的。所以OpenGL中提供了模型观测变换，它是把模型坐标系直接转换为相机坐标系，如图4。现在我们已经计算得到了VC-1和MC，如果把VC-1和MC相乘，就可以得到模型坐标在相机坐标中的表示。为了得到模型坐标系中的坐标在相机坐标系中的表示，这就是OpenGL中的ModelView变换矩阵。这也是ModelView变换的名字的由来，它是通过了上面两个步骤得到的。那么这里，ModelView变换矩阵M为：

\[ M = VC^{-1} \cdot MC \left[ \begin{array}{ccc} 1 & 0 & -5 \\ 0 & -1 & 2 \\ 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{ccc} -1 & 0 & 4 \\ 0 & 1 & 3 \\ 0 & 0 & 1 \end{array} \right] = \left[ \begin{array}{ccc} -1 & 0 & -1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{array} \right] \]

现在只要用上面的模型观测矩阵M乘以模型坐标系MC中的坐标就可以得到相机坐标系中的坐标了。模型观测变换的关键就是要得到相机坐标系中的坐标，因为光照等计算都是在这个这个坐标系中完成的。下面我们实际OpenGL程序中检查一下。在程序中，为了计算方便，我们使用图4中的模型。

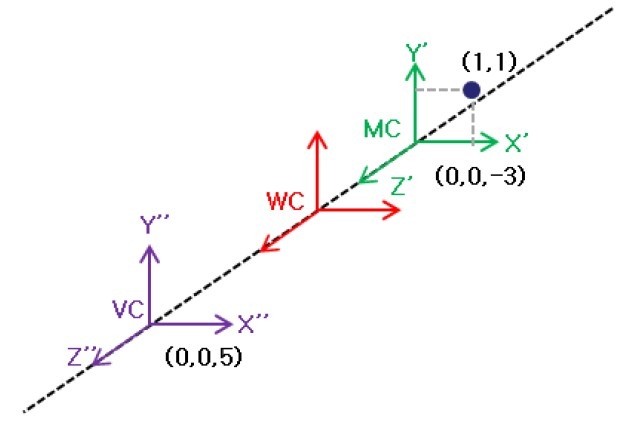
根据图中的数据，我们分别可以写出对应MC和\(VC^{-1}\)，从而求得观测变换矩阵M。

\[ MC = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & -3\\ 0 & 0 & 1 & 1\end{array} \right] VC^{-1} = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & -5\\ 0 & 0 & 1 & 1\end{array} \right] \]

\[ M = VC^{-1} \cdot MC \left[ \begin{array}{ccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & -8\\ 0 & 0 & 1 & 1\end{array} \right] \]

总结####

ModelView 变换矩阵，就是完成从Model坐标到View坐标的转换。注意，modelview 既有model，也有view。
OpenGL的程序中通过glTranslatef(); glScaled(); glRotatef);函数来控制Model变换矩阵；
OpenGL的程序中通过gluLookAt();函数来控制View变换矩阵；
以上四个函数共同作用ModelView变换矩阵。
这里附上测试程序：

    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
    glTranslatef(0, 0, -3);
    glGetFloatv(GL_MODELVIEW_MATRIX, m);
    str = "MC = ";
    output(str);

    glLoadIdentity();
    gluLookAt(0.0, 0.0, 5.0,
              0.0, 0.0, 0.0,
              0.0, 1.0, 0.0);
    glGetFloatv(GL_MODELVIEW_MATRIX, m);
    str = "VC^-1 = ";
    output(str);

    glLoadIdentity();
    glTranslatef(0, 0, -3);
    gluLookAt(0.0, 0.0, 5.0,
              0.0, 0.0, 0.0,
              0.0, 1.0, 0.0);
    glGetFloatv(GL_MODELVIEW_MATRIX, m);
    str = "M = ";
    output(str);

输出如下图：

1.2投影变换(Projection Transformation)###

图1中可以看到，在投影变换(Projection Transformation)中也分为两个部分，第一个部分是将上个阶段得到的坐标转换为平面坐标，第二个部分是将转换后的平面坐标在进行归一化并进行剪裁。一般地，将三维坐标转换为平面坐标有两种投影方式：正交投影(Orthogonal Projection)和透视投影(Perspective Projection)。

1.2.1 正交投影(Othogonal Projection)####

正交投影很简单，如图5，对于三维空间中的坐标点和一个二维平面，要在对应的平面上投影，只需将非该平面上的点的坐标分量改为该平面上的坐标值，其余坐标不变。

比如将点(1,1,5)正交投影到z=0的平面上，那么投影后的坐标为(1,1,0)。在openGL中，设置正交投影可以使用函数:

glOrtho (GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble zNear, GLdouble zFar)  

该函数可以设置正交投影的投影空间，在该空间以外的坐标点就不会被投影到投影平面上。函数中的六个参数分是投影空间六个平面，如图6:

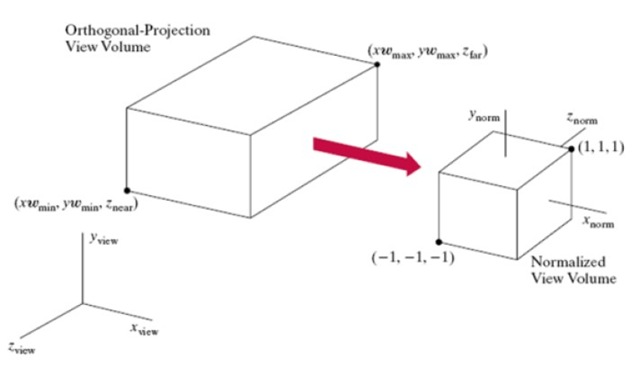
在图6中，大的投影空间是根据这六个参数设置的投影空间，OpenGL会自动将该空间归一化，也就是将该空间或立方体转化为变长为1的正六面体投影空间，并且该证六面体的中心在相机坐标系的原点。一旦设置使用glortho函数设置投影空间，OpenGL会生成投影矩阵。这个矩阵的作用就是将坐标进行正交投影并且将投影后的坐标正规化(转换到-1到1之间)。要注意的是，生成该矩阵的时候，OpenGL会把右手坐标系转换为左手坐标系。原因很简单，右手坐标系的Z轴向平面外的，这样不符合我们的习惯。该矩阵的矩阵推导这里就不详细说明了，不了解的同学可以参考游戏数学方面资料，这里只给出正交投影矩阵。

\[ Mortho = \left[ \begin{array}{ccc} \frac{2}{x_{max}-x_{min}} & 0 & 0 & -\frac{x_{max}+x_{min}}{x_{max}-x_{min}} \\ 0 & \frac{2}{y_{max}-y_{min}} & 0 & -\frac{y_{max}+y_{min}}{y_{max}-y_{min}}\\ 0 & 0 & -\frac{2}{z_{near}-z_{far}} & \frac{z_{near}+z_{far}}{z_{near}-z_{far}}\\ 0 & 0 & 0 & 1\end{array} \right] \]

这个矩阵看来很复杂，其实计算很简单。举个例子，现在设置了这样的正交投影空间glOrtho(-10,10,-10,10,-10,10)，这是个正六面体空间，变长为10。把这些参数带入上面的矩阵可以得到:

\[ Mortho = \left[ \begin{array}{ccc} 0.1 & 0 & 0 & 0 \\ 0 & 0.1 & 0 & 0\\ 0 & 0 & 0.1 & 0\\ 0 & 0 & 0 & 1\end{array} \right] \]

给出代码如下：

    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    glOrtho(-10,10,-10,10,-10,10);
    glGetFloatv(GL_PROJECTION_MATRIX,m);
    str = "Mortho=";
    output(str);

输出结果：

1.2.2透视投影(Perspective Projection)###

透视投影和正交投影最大的区别就是透视投影具有远近感。

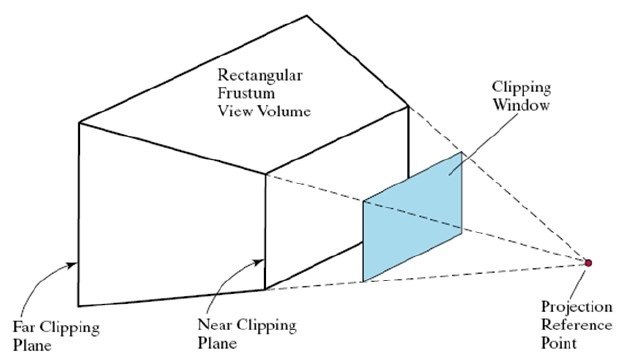
透视投影采用了上图中的模型，这样的模型就是保证远的物体看起来小，近的物体看起来大。 在OpenGL中设置透视投影可以使用函数:

void APIENTRY gluPerspective (GLdouble fovy, GLdouble aspect, GLdouble zNear, GLdouble zFar);
//fovy是眼睛上下睁开的幅度，角度值，值越小，视野范围越狭小（眯眼），值越大，视野范围越宽阔（睁开铜铃般的大眼）。
//zNear表示近裁剪面到眼睛的距离。
//zFar表示远裁剪面到眼睛的距离，注意zNear和zFar不能设置设置为负值（你怎么看到眼睛后面的东西）。
//aspect表示裁剪面的宽w高h比，这个影响到视野的截面有多大。

该函数也会根据给定的参数生成一个投影空间。如上中，该投影空间是一个截头体。同样地，OpenGL会自动生成透视投影矩阵，该矩阵也会让3D坐标投影在投影平面上，并且将投影后的坐标也进行正规化。下面也直接给出OpenGL中使用的透视投影矩阵。

\[ Mpersp = \left[ \begin{array}{ccc} \frac{cot(\frac{\theta}{2})}{x_{max}-x_{min}} & 0 & 0 & 0 \\ 0 & cot(\frac{\theta}{2} & 0 & 0 \\ 0 & 0 & \frac{z_{near}+z_{far}}{z_{near}-z_{far}} & -2\frac{z_{near}z_{far}}{z_{near}-z_{far}}\\ 0 & 0 & -1 & 0\end{array} \right] \]

代码如下：

    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    gluPerspective(45, 1.0, 1.0, 100);
    glMatrixMode(GL_MODELVIEW);
    glGetFloatv(GL_PROJECTION_MATRIX,m);
    str = "Mpersp=";
    output(str);

输出结果：

1.3视口变换(View port Transformation)###

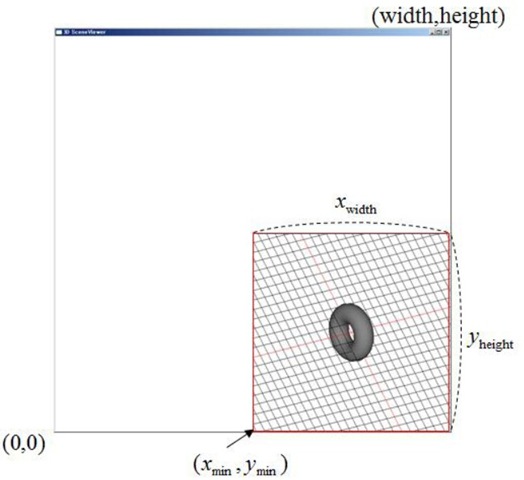
视口变换是把上个阶段得到的正规化的投影坐标转化为windows 窗口坐标。视口变换会将投影平面上的画面映射到窗口上。在OpenGL中可以使用函数

GLAPI void GLAPIENTRY glViewport (GLint x, GLint y, GLsizei width, GLsizei height); 

来进行对窗口的映射，如图: