SLAM中的李群李代数

个人理解

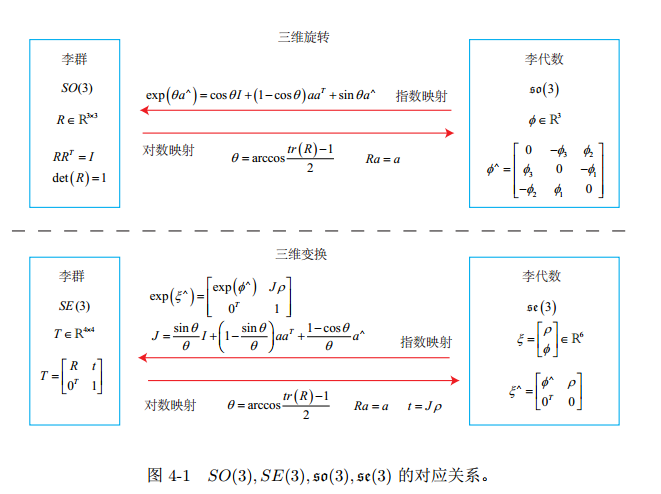
SLAM的李群和李代数的应用体现在旋转矩阵和旋转向量上：旋转矩阵对应李群，旋转向量对应李代数。
在现代微分几何中李群一种流形（Manifold），单位元处的正切空间代表了这个李群的李代数空间。
旋转本身有3个自由度。旋转向量就可以完整表示。
旋转矩阵是3x3的，有9个变量，变量之间是有约束关系的（正交矩阵），对于旋转的表示存在变量冗余。
在SLAM的非线性优化中，旋转（位姿中）中作为一种节点参与优化，需要对其求偏导。
对矩阵求偏导相对复杂，且旋转矩阵这种带有自身约束和变量冗余的表示方法，放到优化中需要添加额外的约束，使得优化变得更加复杂。
然而，利用旋转向量参与优化，就很好的解决了上述问题。

映射关系

BCH公式

\[ln(exp(\phi_1^\wedge)exp(\phi_2^\wedge))\approx \begin{cases} J_l(\phi_2)^{-1}\phi_1+\phi_2, \text{if $\phi_1$ is small} \\ J_r(\phi_1)^{-1}\phi_2+\phi_1, \text{if $\phi_2$ is small} \end{cases} \\ exp((\phi+\Delta \phi)^\wedge)\approx exp((J_l \Delta \phi)^\wedge)exp(\phi^\wedge)\approx exp(\phi^\wedge)exp((J_r\Delta\phi)^\wedge) \\ exp(\Delta \xi^\wedge)exp(\xi^\wedge)\approx exp((J_l^{-1}\Delta\xi+\xi)^\wedge) \\ exp(\xi^\wedge)exp(\Delta\xi^\wedge)\approx exp((J_r^{-1}\Delta\xi+\xi)^\wedge) \]

李代数求导

\[\frac {\partial Rp}{\partial \phi} = -(Rp)^\wedge \]