常见的imu为MEMS,使用硅微加工技术制造,使用科氏力。
误差模型
m(t)=mt(t)+bias(t)+ϵ(t)˙bias(t)=nb(t)
- 固定偏差bias,作为状态量估计
- 白噪声ϵ(t)积分成角度随机游走,连续时间标准差σ(标定结果)除以sqrt(δ(t))得到离散标准差
- bias随机游走,连续时间随机游走(标定结果)乘以sqrt(δ(t))得到离散随机游走
预积分
第i时刻到第j时刻,根据imu的离散读数,推出角度、速度和位置的变化。
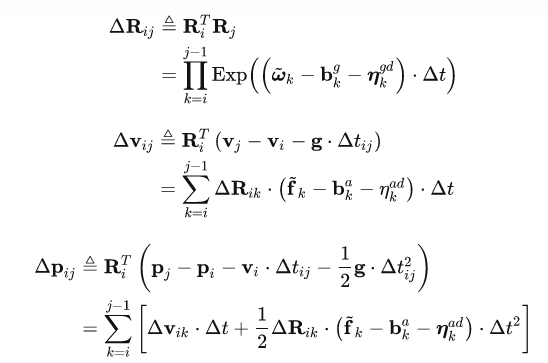
噪声分离
根据imu的噪声,推出预积分的噪声,进而得到预积分的信息矩阵(协方差的逆)
预积分真值 = 测量值 - 误差
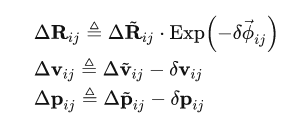
预积分误差

imu的噪声->预积分噪声
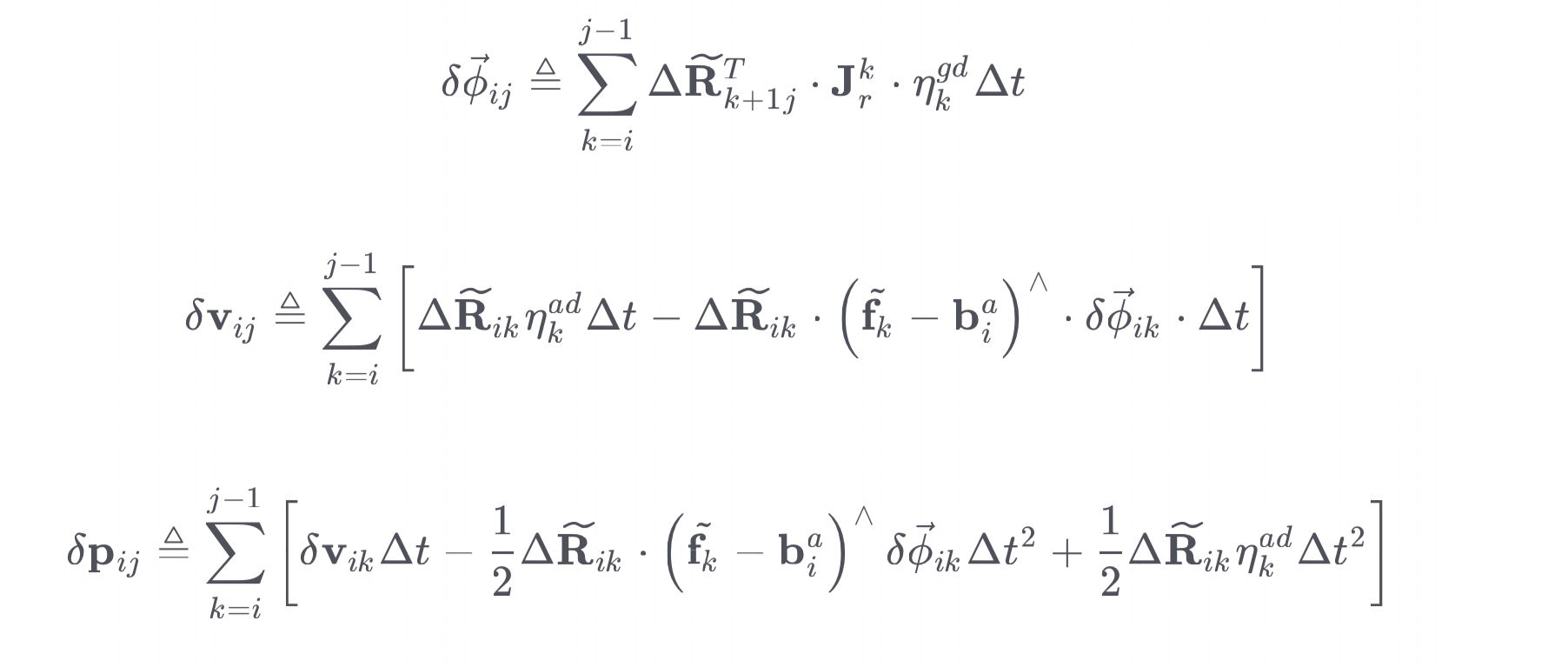
噪声递推
根据上一时刻的预积分误差递推下一时刻预积分误差,从而获取协方差递推
imu误差
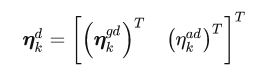
预积分误差

预积分递推
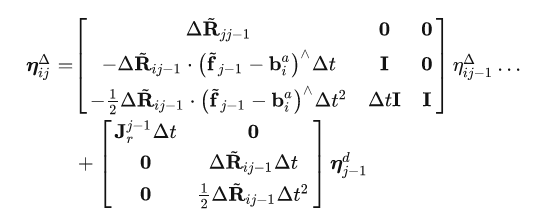
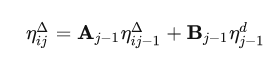
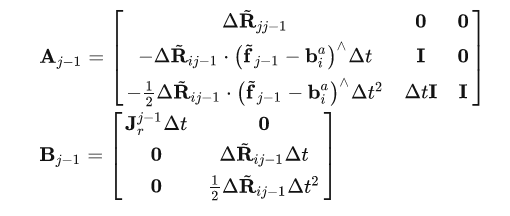
协方差矩阵递推
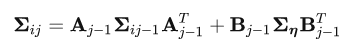
bais更新->预积分更新
新的bias:^bgi ^baa 由旧的bias:¯¯¯¯bgi ¯¯¯¯bai和变化量δbgi和δbai相加得到:即
^bgi←¯¯¯¯bgi+δbgi^bai←¯¯¯¯bai+δbai
预积分关于bais变化的一阶近似更新公式
~Rij(^bgi)≈Δ~Rij(¯¯¯¯bgi)⋅Exp(∂Δ¯¯¯¯¯Rij∂¯¯¯¯bgδbgi)~vij(^bgi,^bai)≈Δ~vij(¯¯¯¯bgi,¯¯¯¯bai)+∂Δ¯¯¯vij∂¯¯¯¯bgδbgi+∂Δ¯¯¯vij∂¯¯¯¯baδbai~pij(^bgi,^bai)≈Δ~pij(¯¯¯¯bgi,¯¯¯¯bai)+∂Δ¯¯¯¯pij∂¯¯¯¯bgδbgi+∂Δ¯¯¯¯pij∂¯¯¯¯baδbai
偏导项
∂Δ¯¯¯¯¯Rij∂¯¯¯¯bg=j−1∑k=i(−Δ¯¯¯¯¯RTk+1jJkrΔt)∂Δ¯¯¯vij∂¯¯¯¯bg=−j−1∑k=i(Δ¯¯¯¯¯Rik⋅(~fk−¯¯¯¯bai)∧∂Δ¯¯¯¯¯Rik∂¯¯¯¯bgΔt)∂Δ¯¯¯vij∂¯¯¯¯ba=−j−1∑k=i(Δ¯¯¯¯¯RikΔt)∂Δ¯¯¯¯pij∂¯¯¯¯bg=j−1∑k=i[∂Δ¯¯¯vik∂¯¯¯¯bgΔt−12Δ¯¯¯¯¯Rik⋅(~fk−¯¯¯¯bai)∧∂Δ¯¯¯¯¯Rik∂¯¯¯¯bgΔt2]∂Δ¯¯¯¯pij∂¯¯¯¯ba=j−1∑k=i[∂Δ¯¯¯vik∂¯¯¯¯baΔt−12Δ¯¯¯¯¯RikΔt2]其中Jkr=Jr((~ωk−bgi)Δt)
残差构建
状态量
Ri,pi,vi,Rj,pj,vj,δbgi,δbai
残差
rΔRij≜log⎧⎨⎩[~Rij(¯¯¯¯bgi)⋅Exp(∂Δ¯¯¯¯¯Rij∂¯¯¯¯bgδbgi)]T⋅RTwiRwj⎫⎬⎭≜log[(Δ^Rij)TΔRij]rΔvij≜RTi(vj−vi−g⋅Δtij)−[Δ~vij(¯¯¯¯bgi,¯¯¯¯bai)+∂Δ¯¯¯vij∂¯¯¯¯bgδbgi+∂Δ¯¯¯vij∂¯¯¯¯baδbai]≜Δvij−Δ^vijrΔpij≜RTi(pj−pi−vi⋅Δtij−12g⋅Δt2ij)−[Δ~pij(¯¯¯¯bgi,¯¯¯¯bai)+∂Δ¯¯¯¯pij∂¯¯¯¯bgδbgi+∂Δ¯¯¯¯pij∂¯¯¯¯baδbai]≜Δpij−Δ^pij
状态更新
Rwi←Rwi⋅Exp(δ→ϕi)pwi←pwi+Rwi⋅δpwivi←vi+δviRwj←Rwj⋅Exp(δ→ϕj)pwj←pwj+Rwj⋅δpwjvj←vj+δvjδbgi←δbgi+˜δbgiδbai←δbai+˜δbai
雅可比
旋转残差
对于Rwi
∂rΔ→ϕij∂δ→ϕi=−J−1r(rΔ→ϕij)RTwjRwi
对于Rwj
∂rΔ→ϕij∂δ→ϕj=J−1r(rΔ→ϕij)
对于~bgi
∂rΔ→φij∂δ~bgi=−J−1r(rΔ→ϕij)⋅Exp(−rΔ→ϕij)⋅Jr(∂Δ˜Rij∂bgδbgi)⋅∂Δ~Rij∂bg
速度残差
对于δ~bgiδ~bai
∂rΔvij∂δ~bgi=−∂Δ~vij∂bg∂rΔvij∂δ~bai=−∂Δ~vij∂ba
对于vi
∂rΔvij∂δvi=−RTwi
对于vj
∂rΔvij∂δvj=RTwi
对于Rwi
∂rΔvij∂δ→ϕi=[RTwi⋅(vj−vi−g⋅Δtij)]
位置残差
对于δ~bgiδ~bai
∂rΔpij∂δ~bgi=−∂Δ~pij∂bg∂rΔpij∂δ~bai=−∂Δ~pij∂ba
对于pwi
∂rΔpij∂δpi=−I
对于pwj
∂rΔpij∂δpj=RTwiRwj
对于vi
∂rΔpij∂δvi=−RTwiΔtij
对于Rwi
∂rΔpij∂δ→ϕi=[RTwi⋅(pwj−pwi−vi⋅Δtij−12g⋅Δt2ij)]
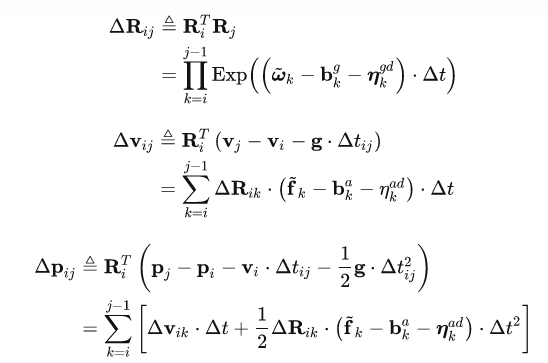
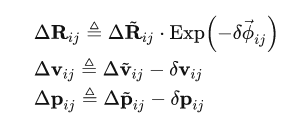

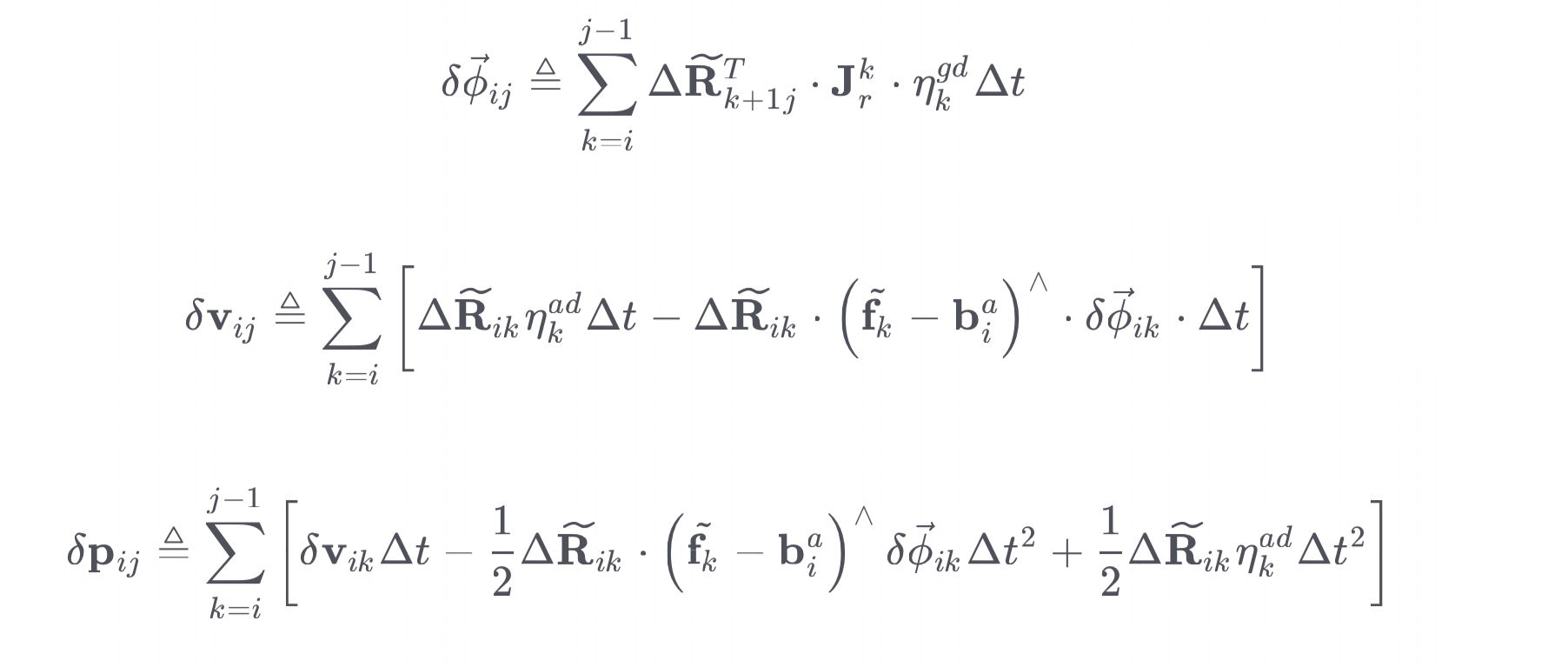
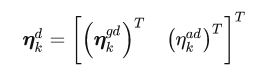

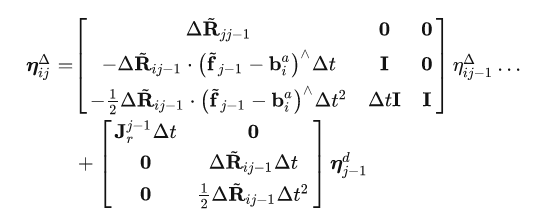
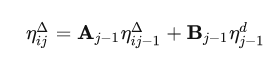
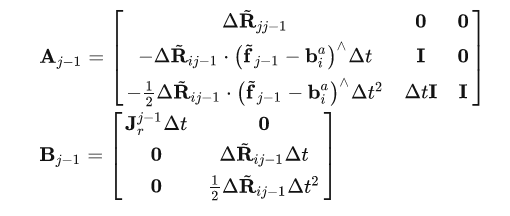
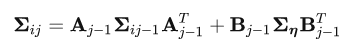




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】