2D-2D:对极几何 基础矩阵F 本质矩阵E 单应矩阵H
对极约束
\[\boldsymbol{x}_{2}^{T} \boldsymbol{F} \boldsymbol{x}_{1}=\boldsymbol{0} \quad \hat{\boldsymbol{x}}_{2}^{T} \boldsymbol{E} \hat{\boldsymbol{x}}_{1}=\mathbf{0}
\]
其中
\[\boldsymbol{E}=\boldsymbol{K}_{2}^{-T} \boldsymbol{F K}_{1} \quad \hat{\boldsymbol{x}}_{1}=\boldsymbol{K}_{1}^{-1} \boldsymbol{x}_{1} \quad \hat{\boldsymbol{x}}_{2}=\boldsymbol{K}_{2}^{-1} \boldsymbol{x}_{2}
\]
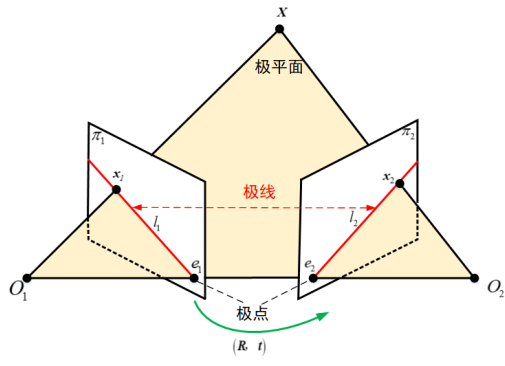
公式推导
\[\boldsymbol{P}_{1}=\boldsymbol{K}_{1}[\boldsymbol{I}, \quad \mathbf{0}] \quad \boldsymbol{P}_{2}=\boldsymbol{K}_{2} \left[ \begin{array}{ll}{\boldsymbol{R},} & {\boldsymbol{t}}\end{array}\right]
\]
\[d_{1} x_{1}=K_{1} X \quad \Rightarrow \quad d_{1} K_{1}^{-1} x_{1}=X=d_{1} \hat{x}_{1}
\]
\[d_{2} \boldsymbol{x}_{2}=\boldsymbol{K}_{2}(\boldsymbol{R} \boldsymbol{X}+\boldsymbol{t}) \Rightarrow \quad d_{2} \boldsymbol{K}_{2}^{-1} \boldsymbol{x}_{2}=\boldsymbol{R} \boldsymbol{X}+\boldsymbol{t}=d_{1} \boldsymbol{R} \hat{x}_{1}+\boldsymbol{t}
\]
\[\quad d_{2}[t]_{\times} \hat{x}_{2}=d_{1}[t]_{\times} R \hat{x}_{1}+[t]_{\times} t
\]
\[\quad d_{2} \hat{x}_{2}^{T}[t]_{\times} \hat{x}_{2}=d_{1} \hat{x}_{2}^{T}[t]_{\times} R \hat{x}_{1}=0
\]
\[\hat{\boldsymbol{x}}_{2}^{T}[\boldsymbol{t}]_{ \times} \boldsymbol{R} \hat{x}_{1}=\hat{\boldsymbol{x}}_{2}^{T} \boldsymbol{E} \hat{x}_{1}=0
\]
\[\boldsymbol{E}=[\boldsymbol{t}]_{ \times} \boldsymbol{R}
\]
\[\boldsymbol{x}_{2}^{T} \boldsymbol{K}_{2}^{-T}[\boldsymbol{t}]_{\times} \boldsymbol{R} \boldsymbol{K}_{1}^{-1} \boldsymbol{x}_{1}=\boldsymbol{x}_{2}^{T} \boldsymbol{F} \boldsymbol{x}_{1}=0
\]
\[\boldsymbol{F}=\boldsymbol{K}_{2}^{-T} \boldsymbol{E} \boldsymbol{K}_{1}^{-1}
\]
基础矩阵性质
-
3x3的矩阵,秩为2
-
具有7个自由度
-
奇异值为\(\left[ \begin{array}{lll}{\sigma_{1},} & {\sigma_{2},} & {0}\end{array}\right]^{T}\)
-
极线约束\(l_{1}=\boldsymbol{x}_{2}^{T} \boldsymbol{F}, \quad l_{2}=\boldsymbol{F} \boldsymbol{x}_{1}, \quad \boldsymbol{x}_{2}^{T} \boldsymbol{F} \boldsymbol{x}_{1}=0\)
基础矩阵求解方法
直接线性变换法 (8点法+最小二乘法)
对于一对匹配点
\[\boldsymbol{x}_{1}=\left[ \begin{array}{ll}{u_{1},} & {v_{1},} & {1}\end{array}\right]^{\mathrm{T}}, \quad \boldsymbol{x}_{2}=\left[ \begin{array}{ll}{u_{2},} & {v_{2},} & {1}\end{array}\right]^{\mathrm{T}}
\]
根据对极约束
\[\boldsymbol{x}_{2}^{T} \boldsymbol{F} \boldsymbol{x}_{1}=\boldsymbol{0}
\]
有
\[\left( \begin{array}{lll}{u_{1}} & {v_{1}} & {1}\end{array}\right) \left[ \begin{array}{ccc}{F_{11}} & {F_{12}} & {F_{13}} \\ {F_{21}} & {F_{22}} & {F_{23}} \\ {F_{31}} & {F_{32}} & {F_{33}}\end{array}\right] \left( \begin{array}{c}{u_{2}} \\ {v_{2}} \\ {1}\end{array}\right)=0
\]
令
\[\boldsymbol{f}=\left[ \begin{array}{lll}{F_{11},} & {F_{12},} & {F_{13}}, \quad \end{array}\right.F_{21}, \quad F_{22}, \quad F_{23}, \quad F_{31}, \quad F_{32}, \quad F_{33} ]^{T}
\]
有约束
\[\left[ \begin{array}{llllll}{u_{1} u_{1},} & {u_{1} v_{2},} & {u_{1},} & {v_{2} u_{1},} & {v_{1} v_{2},} & {v_{1},} & {u_{2},} & {v_{2},} & {1}\end{array}\right] f=0
\]
当有n对匹配点时
\[A=\left( \begin{array}{ccccccccc}
{\begin{array}{l}
{u_{1}^{(1)} u_{1}^{(1)}, \quad u_{1}^{(1)} v_{2}^{(1)}, \quad u_{1}^{(1)}, \quad v_{1}^{(1)} u_{2}^{(1)}, \quad v_{1}^{(1)} v_{2}^{(1)}, \quad v_{1}^{(1)}, \quad u_{2}^{(1)}, \quad v_{2}^{(1)}, \quad 1}
\\ {u_{1}^{(2)} u_{1}^{(2)}, \quad u_{1}^{(2)} v_{2}^{(2)}, \quad u_{1}^{(2)}, \quad v_{1}^{(2)} u_{2}^{(2)}, \quad v_{1}^{(2)} v_{2}^{(2)}, \quad v_{1}^{(2)}, \quad u_{2}^{(2)}, \quad v_{2}^{(2)}, \quad 1}
\\ \quad \vdots \quad\quad \quad \vdots \quad\quad \quad \vdots\quad \quad\quad \vdots \quad \quad\quad \vdots \quad\quad \vdots\quad \quad \vdots\quad\quad \quad \vdots\quad\quad \vdots
\\u_{1}^{(n)} u_{1}^{(n)}, \quad u_{1}^{(n)} v_{2}^{(n)}, \quad u_{1}^{(n)}, \quad v_{1}^{(n)} u_{2}^{(n)}, \quad v_{1}^{(n)} v_{2}^{(n)}, \quad v_{1}^{(n)}, \quad u_{2}^{(n)}, \quad v_{2}^{(n)}, \quad 1
\end{array}}
\end{array}\right).
\]
\[A f=0
\]
- 要保证有唯一解至少需要8对匹配点
- n = 8时,若A非奇异,则有唯一解,称为8点法
- n >= 8时,可用最小二乘法求解( $ A^TA $ 的最小特征值对应的特征向量即为最优解)
奇异值约束
直接线性变化法无法保证基础矩阵的奇异值约束—有两个非0奇异值
根据奇异值约束对矩阵进行重构
\[\min \|\boldsymbol{F}-\hat{\boldsymbol{F}}\|, \quad \text { wrt. } \operatorname{svd}(\boldsymbol{F})=\left[ \begin{array}{lll}{\sigma_{1},} & {\sigma_{2},} & {0}\end{array}\right]
\]
对得到的基础矩阵进行奇异值分解
\[\hat{\boldsymbol{F}}=\boldsymbol{U S V}^{T} \quad \text { with } S=\operatorname{diag}\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)
\]
利用奇异值约束对基础矩阵进行重构
\[\boldsymbol{F}=\boldsymbol{U} \operatorname{diag}\left(\sigma_{1}, \quad \sigma_{2}, \quad 0\right) \boldsymbol{V}^{T}
\]
RANSAC-估计基础矩阵
算法流程
- 随机采样8对匹配点
- 8点法求解基础矩阵
- 奇异值约束获取基础矩阵
- 计算误差,并统计内点个数
- 重复上述过程,选择内点数最多的结果
- 对所有内点执行2,3,重新计算
内点判断标准-Sampson Distance
\[\begin{array}{c}{d\left(\boldsymbol{x}_{1}, \boldsymbol{x}_{2}\right)=\frac{\left(\boldsymbol{x}_{2}^{T} \boldsymbol{F} \boldsymbol{x}_{1}\right)^{2}}{\left(\boldsymbol{F} x_{1}\right)_{x}^{2}+\left(\boldsymbol{F} x_{1}\right)_{x}^{2}+\left(\boldsymbol{x}_{2}^{T} \boldsymbol{F}\right)_{x}^{2}+\left(\boldsymbol{x}_{2}^{T} \boldsymbol{F}\right)_{y}^{2}}} \\ {d\left(\boldsymbol{x}_{1}, \boldsymbol{x}_{2}\right)<\tau}\end{array}
\]
RANSAC-采样次数的计算
N - 样本点个数
K - 求解模型需要最少的点的个数
p - 表示内点的概率
\[K 个点都是内点概率 p^{K}
\]
\[K个至少有一个外点(采样失败)的概率1-p^{K}
\]
\[M次采样全部失败的概率\left(1-p^{K}\right)^{M}
\]
\[M次采样至少有1次成功的概率 \quad z=1-\left(1-p^{K}\right)^{M}
\]
\[采样次数 \quad M=\frac{\log (1-z)}{\log \left(1-p^{K}\right)}
\]
\[计算p=0.9, \quad K=8 , 时,想要采样
成功率达到 z \geq 0.99, 所需要的采样
次数 M
\]
本征矩阵E性质
-
3x3的矩阵,秩为2
-
具有5个自由度
-
奇异值为\(\left[ \begin{array}{lll}{\sigma,} & {\sigma,} & {0}\end{array}\right]^{T}\)
求解本征矩阵
\[先求解基础矩阵F
\]
\[\widehat{\boldsymbol{E}}=\boldsymbol{K}_{2}^{T} \boldsymbol{F} \boldsymbol{K}_{1}
\]
\[\widehat{\boldsymbol{E}}=\boldsymbol{U} \operatorname{diag}\left(\sigma_{1}, \quad \sigma_{2}, \quad 0\right) \boldsymbol{V}^{T}
\]
\[\boldsymbol{E}=\boldsymbol{U} \operatorname{diag}\left(\frac{\sigma_{1}+\sigma_{2}}{2}, \quad \frac{\sigma_{1}+\sigma_{2}}{2}, \quad 0\right) \boldsymbol{V}^{T}
\]
相机姿态的恢复
求解Rt
\[\boldsymbol{E}=\boldsymbol{U} \Sigma \boldsymbol{V}^{T}, \boldsymbol{\Sigma}=\operatorname{diag}(\sigma, \quad \sigma, \quad 0)
\]
\[t_{1}=U( :, 2) \quad R_{1}=U R_{Z}\left(\frac{\pi}{2}\right) V^{T}
\]
\[\boldsymbol{t}_{2}=-\boldsymbol{U}( :, \boldsymbol{2}) \quad \boldsymbol{R}_{2}=\boldsymbol{U} \boldsymbol{R}_{\mathrm{Z}}^{T}\left(\frac{\pi}{2}\right) \boldsymbol{V}^{T}
\]
\[\boldsymbol{R}_{z}\left(\frac{\pi}{2}\right)=\left( \begin{array}{ccc}{0,} & {-1,} & {0} \\ {1,} & {0,} & {0} \\ {0,} & {0,} & {1}\end{array}\right), \boldsymbol{R}_{z}^{T}\left(\frac{\pi}{2}\right)=\left( \begin{array}{ccc}{0,} & {1,} & {0} \\ {-1,} & {0,} & {0} \\ {0,} & {0,} & {1}\end{array}\right)
\]
\[共有4种情况 \left(\boldsymbol{R}_{1}, \boldsymbol{t}_{1}\right),\left(\boldsymbol{R}_{1}, \boldsymbol{t}_{2}\right),\left(\boldsymbol{R}_{2}, \boldsymbol{t}_{1}\right),\left(\boldsymbol{R}_{2}, \boldsymbol{t}_{2}\right)
\]
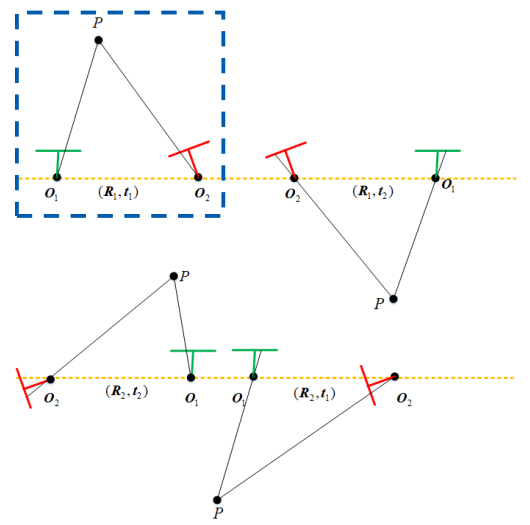
选择正确的Rt
相机的世界坐标
\[\boldsymbol{O}_{1}=-\boldsymbol{R}^{T} \boldsymbol{t}=0, \quad \boldsymbol{O}_{2}=-\boldsymbol{R}^{T} \boldsymbol{t}
\]
相机的世界坐标中的朝向
\[d_{1}=\left[ \begin{array}{lll}{0,} & {0} & {1}\end{array}\right]^{T}
\]
\[\boldsymbol{d}_{2}=\left[ \begin{array}{cccc}{\boldsymbol{r}_{1}^{T}} & {\boldsymbol{r}_{2}^{T}} & {\boldsymbol{r}_{3}^{T}} & {-\boldsymbol{R}^{T} \boldsymbol{t}}\end{array}\right]\left[ \begin{array}{l}{0} \\ {0} \\ {1} \\ {0}\end{array}\right]=r_{3}^{T}
\]
\[\boldsymbol{R}=\left[ \begin{array}{c}{\boldsymbol{r}_{1}} \\ {\boldsymbol{r}_{2}} \\ {\boldsymbol{r}_{3}}\end{array}\right] \quad \boldsymbol{R}^{T}=\left[ \begin{array}{ccc}{\boldsymbol{r}_{1}^{T}} & {\boldsymbol{r}_{2}^{T}} & {\boldsymbol{r}_{3}^{T}}\end{array}\right]
\]
利用相机姿态和匹配点进行三角量测得到三维点P
P需满足同时位于两个相机的前方:
方法1:
\[\begin{array}{l}{\left(\boldsymbol{P}-\boldsymbol{O}_{1}\right)^{T} \boldsymbol{d}_{1}>0} \\ {\left(\boldsymbol{P}-\boldsymbol{O}_{2}\right)^{T} \boldsymbol{d}_{1}>0}\end{array}
\]
方法2:
\[\left[ \begin{array}{l}{x_{c}} \\ {y_{c}} \\ {z_{c}}\end{array}\right]=\boldsymbol{R P}+\boldsymbol{t}, \quad Z_{c}>0 对两个相机成立
\]
单应矩阵H
即单应矩阵有两种情况:
1.空间点位于平面
2.相机纯旋转
空间中特征点位于一平面上
\[\boldsymbol{n}^{T} \boldsymbol{X}+d=0 \quad \Rightarrow \quad-\frac{\boldsymbol{n}^{T} \boldsymbol{X}}{d}=1
\]
\[\begin{equation}
\begin{aligned}
\boldsymbol{x}_{2}
&= \boldsymbol{K}_{2}(\boldsymbol{R} \boldsymbol{X}+\boldsymbol{t})\\
&=\boldsymbol{K}_{2}\left(\boldsymbol{R} \boldsymbol{X}+\boldsymbol{t} \cdot\left(-\frac{\boldsymbol{n}^{T} \boldsymbol{X}}{d}\right)\right)\\
&=\boldsymbol{K}_{2}\left(\boldsymbol{R}-\frac{t \boldsymbol{n}^{T}}{d}\right) \boldsymbol{X} \\
&=\boldsymbol{K}_{2}\left(\boldsymbol{R}-\frac{t \boldsymbol{n}^{T}}{d}\right) \boldsymbol{K}_{1}^{-1} \boldsymbol{x}_{1}
\end{aligned}
\end{equation}
\]
\[\boldsymbol{x}_{2}=\boldsymbol{H} \boldsymbol{x}_{1}, \quad \boldsymbol{H}=\boldsymbol{K}_{2}\left(\boldsymbol{R}-\frac{\boldsymbol{t} \boldsymbol{n}^{T}}{d}\right) \boldsymbol{K}_{1}^{-1}
\]
单应矩阵是满秩的
\[x_{1}=H^{-1} x_{2}
\]
t = 0时,对应纯旋转
\[\boldsymbol{H}=\boldsymbol{K}_{2} \boldsymbol{R} \boldsymbol{K}_{1}^{-1}
\]
单应矩阵求法
直接线性变换法
\[\left( \begin{array}{c}{u_{2}} \\ {v_{2}} \\ {1}\end{array}\right)=\left[ \begin{array}{lll}{H_{11}} & {H_{12}} & {H_{13}} \\ {H_{21}} & {H_{22}} & {H_{23}} \\ {H_{31}} & {H_{32}} & {H_{33}}\end{array}\right] \left( \begin{array}{l}{u_{1}} \\ {v_{1}} \\ {1}\end{array}\right)
\]
\[\begin{aligned}
u_{2} &=\frac{H_{11} u_{1}+H_{12} v_{1}+H_{13}}{H_{31} u_{1}+H_{32} v_{1}+H_{33}} \\
v_{2}& = \frac{H_{21} u_{1}+H_{22} v_{1}+H_{23}}{H_{31} u_{1}+H_{32} v_{1}+H_{33}} \end{aligned}
\]
8个自由度,每对点有两个约束
\[H_{11} u_{1}+H_{12} v_{1}+H_{13}-H_{31} u_{1} u_{2}-H_{32} u_{2} v_{1}-H_{33} u_{2}=0\\
H_{21} u_{1}+H_{22} v_{1}+H_{23}-H_{31} u_{1} v_{2}-H_{32} v_{1} v_{2}-H_{33} v_{2}=0
\]
令 \(H_{33}=1\)总共需要4对特征点
\[A=\left( \begin{array}{c}
u_{1}^{(1)}, \quad v_{1}^{(1)}, \quad 1, \quad 0, \quad 0, \quad 0, \quad-u_{1}^{(1)} u_{2}^{(1)}, \quad-u_{2}^{(1)} v_{1}^{(1)} \\
0, \quad 0, \quad 0, \quad u_{1}^{(1)}, \quad v_{1}^{(1)}, \quad 1, \quad-u_{1}^{(1)} v_{2}^{(1)}, \quad-v_{1}^{(1)} v_{2}^{(1)}\\
{\vdots} \\
u_{1}^{(4)}, \quad v_{1}^{(4)}, \quad 1, \quad 0, \quad 0, \quad 0, \quad-u_{1}^{(4)} u_{2}^{(4)}, \quad-u_{2}^{(4)} v_{1}^{(4)} \\
0, \quad 0, \quad 0, \quad u_{1}^{(1)}, \quad v_{1}^{(1)}, \quad 1, \quad-u_{1}^{(4)} v_{2}^{(4)}, \quad-v_{1}^{(4)} v_{2}^{(4)}\end{array}\right)
\left( \begin{array}{c}{F_{11}} \\ {F_{12}} \\ {F_{13}} \\ {F_{21}} \\ {F_{21}} \\ {F_{22}} \\ {F_{33}} \\ {F_{31}} \\ {F_{32}}\end{array}\right)
=\left( \begin{array}{c}{u_{2}^{(1)}} \\ {v_{2}^{(1)}} \\ {u_{2}^{(2)}} \\ {v_{2}^{(2)}} \\ {v_{2}^{(2)}} \\ {u_{2}^{(3)}} \\ {v_{2}^{(4)}} \\ {v_{2}^{(4)}} \\ {v_{2}^{(4)}}\end{array}\right)
\]
RANSAC-估计单应矩阵
算法流程
- 随机采样4对匹配点\(\left(x_{1}^{(n)}, x_{2}^{(n)}\right)\)
- 8点法求解基础矩阵H
- 计算误差,并统计内点个数
- 重复上述过程,选择内点数最多的结果
- 对所有内点执行3,4,重新计算H
内点判断标准
\[E\left(x_{1}, x_{2}, H\right)=d\left(x_{1}, H^{-1} x_{2}\right)^{2}+d\left(x_{2}, H x_{1}\right)^{2} \\
E\left(x_{1}, x_{2}, H\right)<\tau
\]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号