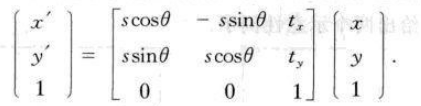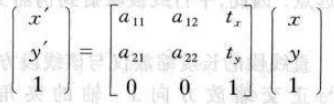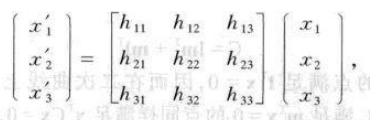等距变换

- \(\epsilon=\pm1\)如果\(\epsilon=1\)那么该等距变换是保向的,即为欧氏变换(平移+旋转)
- 3个自由度
相似变换
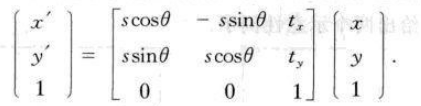
仿射变换
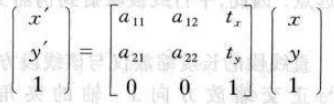
- A是一个2×2的非奇异矩阵,总能分解为$ A = R(\theta)R(-\phi)DR(\phi)$
- \(R(\theta)R(\phi)\)表示旋转角为\(\theta \phi\)的旋转
- D为对角矩阵\(D = \begin{bmatrix}\lambda_1 &0 \\ 0 & \lambda_2 \end{bmatrix}\)
- 分解式可由SVD分解给出 \(A = UDV^T = (UV^T)(VDV^T) = R(\theta)(R(-\phi)DR(\phi))\)
- 仿射变换可以看成先一个旋转\(\phi\) 再在旋转后的xy方向上按比例因子\(\lambda_1 \lambda_2\)的缩放,再加上一个回旋 \(-\phi\),最后再加一个旋转\(\theta\)
- 6个自由度
射影变换
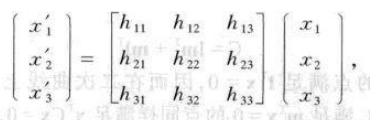
- H矩阵乘以一个非零比例因子不会使射影变换改变,是一个齐次矩阵,有8个自由度
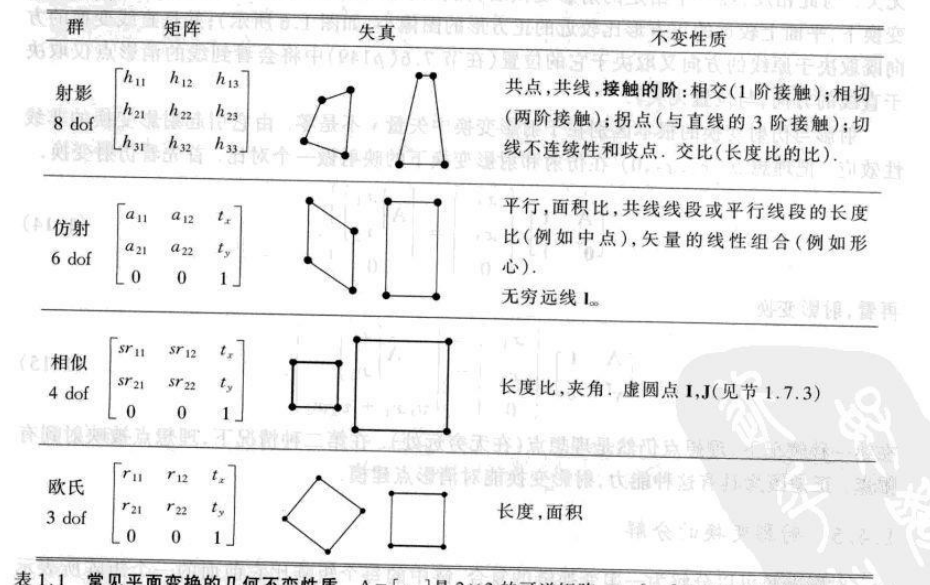
小结
posted @
2019-01-23 01:21
narjaja
阅读(
734)
评论()
编辑
收藏
举报