python解决缔合勒让德函数的递推(标准向前行递推算法)

　　在求解拉普拉斯面球谐函数时存在勒让德方程，而勒让德函数为勒让德方程的解。勒让德函数，通常以符号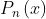表 示，ｎ为阶数，它满足于勒让德微分方程（1）。

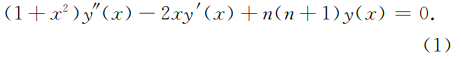
　　完全规格化缔合勒让德函数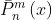是对缔合勒让德函数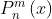进行规格化后的结果，而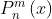则是通过勒让德函数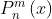计算得到的。θ为球坐标系下的一个坐标量，θ∈［０°，１８０°］，也称为天顶距；ｎ、ｍ均为０或正整数，分别称为函数的阶、次，且ｎ≥ｍ。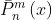常用的递推算法主要有４种：标准向前列递推算法、标准向前行递推算法、跨阶次递推算法和Ｂｅｌｉｋｏｖ递推算法。

　　在本次作业中，我使用的是“标准向前行递推算法”，其算法模型如下式：

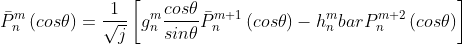
　　式中，ｎ≥２且ｎ＞ｍ，其余参数如下：

 

 

 

 

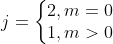
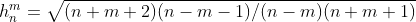
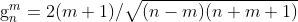
 　　采用python编写，输入所需的n和m，计算θ=36°时对应的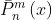，迭代至n=1000，代码如下：

def Lengendre():
    n = float(input('n='))
    m = float(input('m='))
    theta = float(36)
    theta = theta*math.pi/180
    p = np.zeros((1005, 1005))
    p[0][0] = float(1)
    p[1][0] = math.sqrt(3)*math.cos(theta)
    p[1][1] = math.sqrt(3)*math.sin(theta)
    for i in range(2,1001):
        for j in range(i,-1,-1):
            if i == j:
                c_mm = math.sqrt((2*j+1)/(2*j))
                p[i][i] = c_mm * math.sin(theta)*p[i-1][i-1]
            else:
                if j == 0:
                    j_j = float(2)
                else:
                    j_j = float(1)
                h_nm = math.sqrt(((i+j+2)*(i-j-1))/((i-j)*(i+j+1)))
                g_nm = 2*(j+1)/(math.sqrt((i-j)*(i+j+1)))
                if h_nm == 0:
                    p[i][j]=(1/math.sqrt(j_j)) * g_nm * math.cos(theta)/math.sin(theta)*p[i][i]
                else:
                    p[i][j]=(1/math.sqrt(j_j)) * (g_nm * math.cos(theta)/(math.sin(theta))*p[i][j+1] - (h_nm * p[i][j+2]))
                    
    print(' L ',' m ',' P ')
    print(int(n),int(m),p[int(n)][int(m)])