Linear Algebra lecture8 note
Compute solution of AX=b (X=Xp+Xn)
rank r
r=m solutions exist
r=n solutions unique
example:
若想方程有解,b1,b2,b3需要满足什么条件? 观察矩阵可知,第三行是前两行的和,所以b1+b2=b3
Solvability Condition on b:
Ax=b is solvable when b is in C (A)
If a combination of Rows of A gives zero row, then the same combination of entries of b must give 0
To find complete solution to AX=b:
1.Xp (particular): set all free variables to zero, solve AX=b for pivot variable
此例中,X2=0,X4=0
2.Xn(nullspace) 上一节已经解出
3.X(complete)=Xp+Xn
以上操作可解释为:
m by n matrix A of rank r(r<=m,r<=n)
Full column of rank(r=n):
所有列均有主元; no free variables; N(A)=zero vector; solution to AX=b is X=Xp which means if solution exists then the solution is unique(0 or 1 solution)
这种情况实际就是,除zero组合之外,列之间的线性组合无法产生零列
Full row of rank(r=m):
所有行均有主元; no zero rows; can solve AX=b for every b; left with n-r(n-m) free variables
Full rank(r=m=n):
N(A)=zero vector; R(行最简形)=I(单位矩阵)
summary:
矩阵的秩决定了方程组解的数目

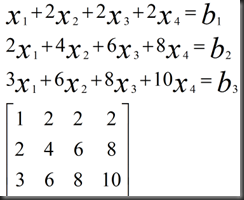
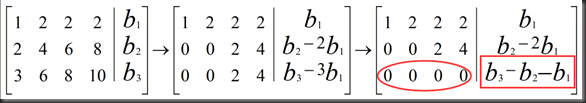
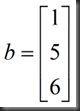

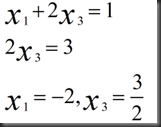
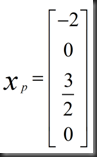
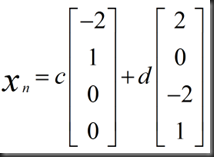
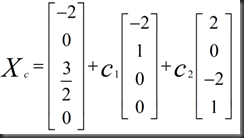



 浙公网安备 33010602011771号
浙公网安备 33010602011771号