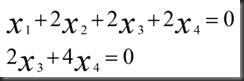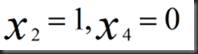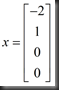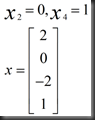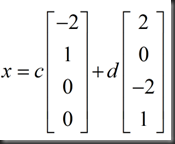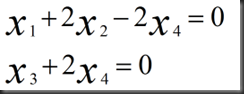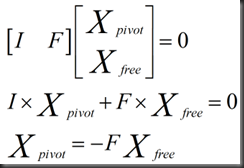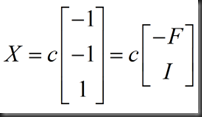Linear Algebra lecture7 note

Computing the nullspace (Ax=0)

Pivot variables-free variables

Special solutions: rref( A)=R

 

---

 

rank of A=the number of pivots=2

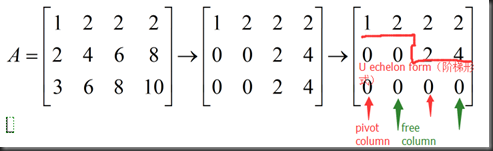
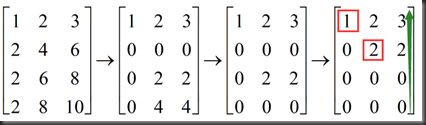
由上述矩阵行变换回代可得方程

我们自行给free variable对应的x赋值

得到一个特解x为

表示的意思是

 

再赋一组值

表示的意思是

以上特解可以组成通解

 

---

 

Reduce row（echelon form：zeros above and below pivots) 行最简形

rref (A) means  (reduced row echelon form of A)

There are some information that this kind of form tells:

1.pivot rows are row1 and row2

2.pivot cols are col1 and col3

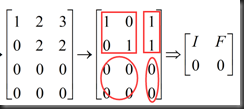
3.this matrix conclude an I（Identity) in it , made by pivot rows and pivot cols

4.全0行表示原行是其他行的线性组合

5.可得知自由列

6.回代得到特解

即我们由AX=0到UX=0，最终得到RX=0

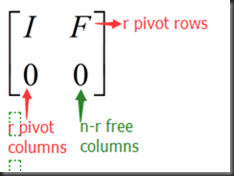
交换R中各列，可得如下形式

rref form：

假设N是RX=0的一个特解

回代：

若Xfree赋值单位矩阵I，那么Xpivot可得到-F

特解与F有关，方程得以解出

example：