[深度学习]数值稳定性+模型初始化和激活函数

数值稳定性+模型初始化和激活函数

1.数值稳定性

• \(t\) 是层数
• \(y\) 是优化函数(不是预测结果)
• 向量关于向量的导数是一个矩阵，那么进行\(d-t\)次矩阵乘法

① MLP：多层感知机。

② 对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵，常写为diag(a1, a2, ..., an)。

③ diag * W 把diag和W分开看。这就是个链式求导，diag是n维度的relu向量对n维度relu的输入的求导，向量对自身求导就是对角矩阵。

1.1.梯度爆炸

解释：

1. 为什么\(W^th^{t-1}\)对\(h^{t-1}\)求导是\((W^t)^T\)?

   这是因为使用了分母布局(结果的行等于分母的大小，即h)

2. 为什么是对角矩阵

   \(\sigma(w^th^{t-1})\)对\(h^{t-1}\)求导，我们可以类比为\(f(x)\)对\(x\)求导，其中\(x\)和\(f(x)\)都是向量

   举个例子：

   \[f(x) = \left[ \begin{matrix} f(x_1)\\ f(x_2) \\ f(x_3) \end{matrix} \right] ,x = \left[ \begin{matrix} x_1\\ x_2 \\ x_3 \end{matrix} \right] \]

那么:

\[\dfrac{\partial f(x)}{\partial x} =\left[ \begin{matrix} \dfrac{\partial f(x)}{\partial x_1}\\ \dfrac{\partial f(x)}{\partial x_2} \\ \dfrac{\partial f(x)}{\partial x_3} \end{matrix} \right] = \left[ \begin{matrix} \dfrac{\partial f(x_1)}{\partial x_1}&\dfrac{\partial f(x_2)}{\partial x_1}&\dfrac{\partial f(x_3)}{\partial x_1}\\ \dfrac{\partial f(x_1)}{\partial x_2}&\dfrac{\partial f(x_2)}{\partial x_2}&\dfrac{\partial f(x_3)}{\partial x_2} \\ \dfrac{\partial f(x_1)}{\partial x_3}&\dfrac{\partial f(x_2)}{\partial x_3}&\dfrac{\partial f(x_3)}{\partial x_3} \end{matrix} \right] = \left[ \begin{matrix} \dfrac{\partial f(x_1)}{\partial x_1}&0&0\\ 0&\dfrac{\partial f(x_2)}{\partial x_2}&0 \\ 0&0&\dfrac{\partial f(x_3)}{\partial x_3} \end{matrix} \right] \]

什么意思呢？

1. 因为对角阵就是由0或1的元素组成的，把这个对角阵和\(W_i^T\)相乘，结果要么是某个\(w\)，要么是\(0\)。

​ 举个例子：

\[\left[ \begin{matrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{matrix} \right] \left[ \begin{matrix} x_1\\ x_2 \\ x_3\end{matrix} \right] = \left[ \begin{matrix} x_1 & x_1 & x_1\\ 0 & 0 & 0 \\ x_3 & x_3 & x_3\end{matrix} \right] \]

2. d-t很大的意思是网络比较深（假设w全是大于1，且层数比较大的话，多层感知机的导数就会非常大）。

1.2.梯度消失

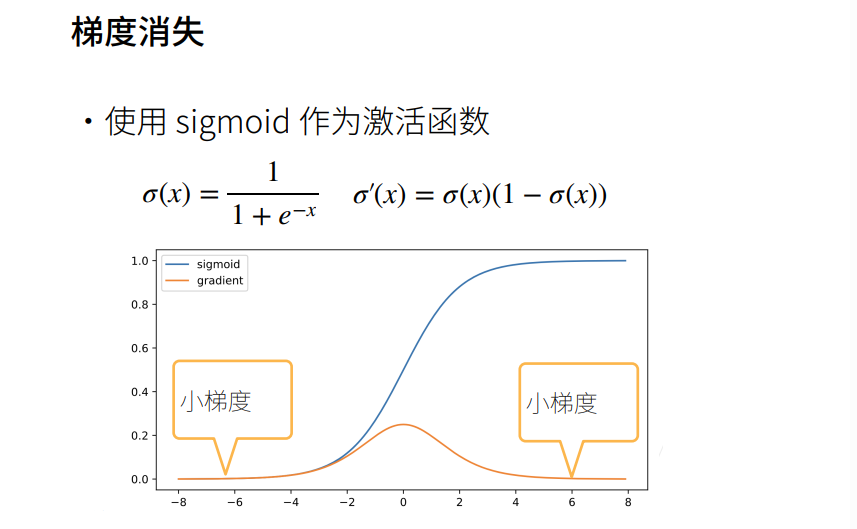
蓝色为原函数，黄色为梯度函数。激活函数的输入稍微大一点时，它的导数就变为接近0，连续n个接近0的数相乘，最后的梯度就接近0，梯度就消失了。

神经网络做梯度是从顶部开始的（顶部是靠近输出层），越到下面（底部）梯度会变得越来越小。意味着不管把神经网络加多深，底部的层都跑不动，也就是说跟一个很浅层的神经网络是没有区别的。这就是梯度消失的问题。

总结

2.模型初始化和激活函数

2.1让训练更加稳定

2.2 正向方差

① 假设权重是独立的同分布，均值为0。

② 假设输入与权重是相互独立的。

推导过程：

假设：

• \(w_{i,j}^t\)是\(i.i,d\)
• \(h_{i}^{t-1}\)独立于\(w_{i,j}^t\)
• 假设没有激活函数\(h^t = W^th^{t-1}\),这里\(W^t\in R^{n_t\times n_{t-1}}\)

\[E[h_{i}^t ] = E[\sum_jw_{i,j}^th_{j}^{t-1}] = \sum_{j}E[w_{i,j}^t]E[h_j^{t-1}] = 0 \]

假设权是独立同分布，\(i,i,d\) 是指一组随机变量中每个变量的概率分布都相同，且这些随机变量互相独立，这一层的输入（h）也是独立于当前的权重。

在第t层的输出的第i个元素的均值可以看成是w的第i行乘以t-1层的输出，对j进行求和，再拆开（独立性、可加性），因为假设两个均值都为0，所以最后等于0。

正向：\(E[h_i^t] = 0,Var[h_i^t] = a\)

\[Var[h_i^t] = E[(h_i^t)^2]-E[h_i^t]^2(方差等于平方项的均值减去均值的平方) \\= E[(\sum_j w_{i,j}^th_j^{t-1})^2]-0(因为均值为0，所以后一项为0)\\ =E[\sum_j(w_{i,j}^t)^2(h_j^{t-1})^2 + \sum_{j\neq k}w_{i,j}^tw_{i,k}^th_j^{t-1}h_{k}^{t-1}]\\ =\sum_jE[(w_{i,j})^2]E[(h_{j}^{t-1})^2]=\sum_j\{E[(w_{i,j})^2]-E[(w_{i,j})]^2\}\times \{E[(h_{j}^{t-1})^2]-E[(h_{j}^{t-1})]^2\}\\ =\sum_j Var[w_{i,j}^t]Var[h_j^{t-1}]=n_{t-1}\gamma_tVar[h_j^{t-1}] \]

要使输入$Var[h_i^t] \(和输出\) n_{t-1}r_tVar[h_j^{t-1}]\(相等的话，\)n_{t-1}\gamma_t = 1$

因为\(n_{t-1}\)是不可改的，是输入的维度，\(\gamma_t\)就是可以选择的方差（因为\(h^t\)是由\(t-1\)层的\(n\)个参数\(w\)运算求得的，而$ t-1 \(层的这些参数之前假设了他们都是服从方差为\)\gamma\(的分布，所以他们相加就成了\)n_{t-1}\gamma_t$）

2.3 反向方差

接下来看方向的情况：

推导过程:

\[Var[\dfrac{\partial l}{\partial h_i^{t-1}}] = E[(\dfrac{\partial l}{\partial h_i^{t-1}})^2]-E[\dfrac{\partial l}{\partial h_i^{t-1}}]^2\\ = E[(\dfrac{\partial l}{\partial h_i^{t}}W_i^t)^2]-E[\dfrac{\partial l}{\partial h_i^{t}}W_i^t]^2\\ = E[(\dfrac{\partial l}{\partial h_i^{t}}W_i^t)^2] = \sum_jE[(\dfrac{\partial l}{\partial h_i^{t}})^2]E[(W_i^t)^2]\\ =\sum_jVar[W_{i,j}^t]Var[\dfrac{\partial l}{\partial h_i^{t}}]\\ = n_t\gamma_tVar[\dfrac{\partial l}{\partial h_i^{t}}] \]

2.4 Xavier 初始

要保证每次前向输出的方差是一致的，要保证梯度是一样的，\(n_{t-1}\)是\(t\)层输入的维度，\(n_t\)是\(t\)层输出的维度，因此无法同时满足这两个条件。
\(\gamma_t\)是第\(t\)层权重的方差，满足输入的维度加输出的维度除以2等于1。xavier初始化的含义就是权重初始的方差是根据输入和输出的维度来决定的。

（注意：以上的推导都是基于没有激活函数的情况）

接下来考虑加入激活函数

为什么输出的均值等于β？
因为是线性变换，输入的均值等于0，则\(\alpha h_{i}'\)等于0。因为β为常数，所以期望等于自身。因此要使期望等于0，则激活函数一定是一条过原点的直线。激活函数的输入和输出的方差有\(\alpha^2\)的关系，也就是激活函数把上一层的输出（也就是这一层的输入）放大α倍的话，方差会放大\(α^2\)倍。如果我不想改变输入输出的方差的话，方法就是使α等于1。
补充：

1. \(E(C) = C\)
2. \(E(CX) = CE[X]\)
3. \(E[X+Y] = E[X]+R[Y]\)
4. 当\(X\)和\(Y\)相互独立时，\(E[XY] = E[X]E[Y]\)

对于反向：

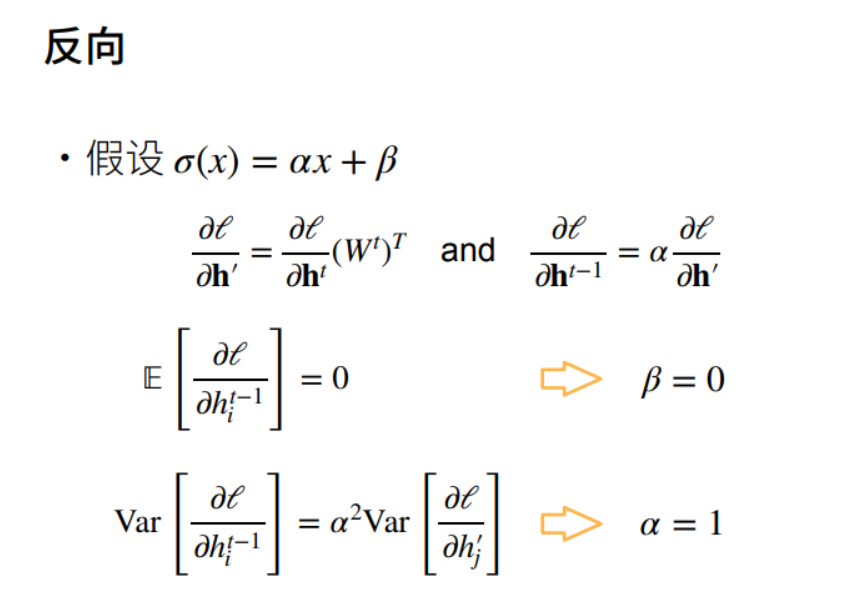
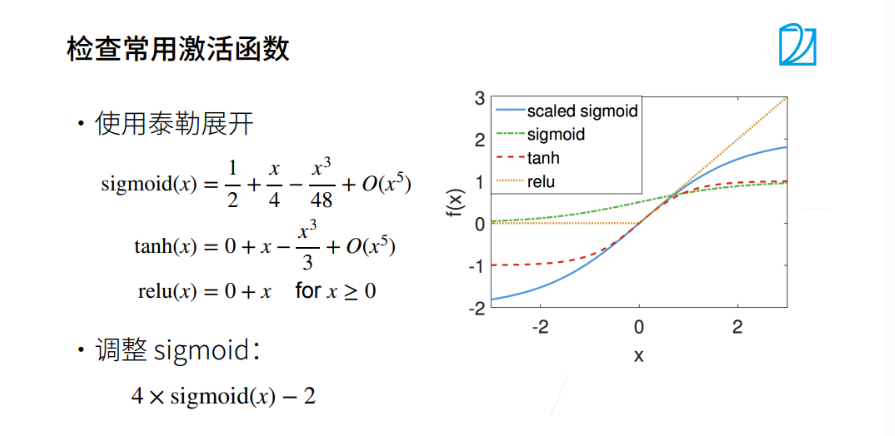
可以从图中看出，tanh和relu都满足在一定区间斜率为1的情况，我们可以调整sigmoid使其满足条件（图中蓝色）。

总结：使得每一层的输出和每一层的梯度都是均值为0，方差为一个固定数的随机变量，权重初始可以是x维，激活函数用relu或者tanh都没问题，使用sigmoid就要对他进行处理。

总结