模型选择、过拟合、欠拟合

在机器学习和统计建模中，模型选择、过拟合和欠拟合是常见的概念，关系到模型的性能和泛化能力。

1.模型选择

举个一个有趣的例子：

惊讶的发现：

你发现所有的5个人在面试的时候都穿了蓝色衬衫(就是咱们说的蓝领嘛)
你的模型也发现了这个强信号
这会有什么问题？

这就引出了我们的训练误差和泛化误差的概念：

1.1训练误差和泛化误差

训练误差：模型在训练数据上的误差
泛化误差：模型在新数据上的误差

问题是，我们永远不能准确地计算出泛化误差。这是因为无限多的数据样本是一个虚构的对象。在实际中，我们只能通过将模型应用于一个独立的测试集来估计泛化误差，该测试集由随机选取的、未曾在训练集中出现的数据样本构成。

例子：根据模考成绩来预测未来考试成绩
- 在过去的考试中表现很好(训练误差)不代表未来考试一定会好(泛化误差)
- 学生A通过背书在模考中拿到好成绩
- 学生B知道答案背后的原因

所以，训练误差的期望小于或等于泛化误差。也就是说，一般情况下，由训练数据集学到的模型参数会使模型在训练数据集上的表现优于或等于在测试数据集上的表现。由于无法从训练误差估计泛化误差，一味地降低训练误差并不意味着泛化误差一定会降低。

机器学习模型应关注降低泛化误差。

1.2验证数据集和测试数据集

验证数据集：一个用来评估模型好坏的数据集
- 例如拿出50%的训练数据
- 不要跟训练数据混在一起（常犯错误）
测试数据集：只用一次的数据集。例如：
- 未来的考试
- 出价房子的实际成交价

从严格意义上讲，测试集只能在所有超参数和模型参数选定后使用一次。不可以使用测试数据选择模型，如调参。由于无法从训练误差估计泛化误差，因此也不应只依赖训练数据选择模型。鉴于此，我们可以预留一部分在训练数据集和测试数据集以外的数据来进行模型选择。这部分数据被称为验证数据集，简称验证集（validation set）。例如，我们可以从给定的训练集中随机选取一小部分作为验证集，而将剩余部分作为真正的训练集。

然而在实际应用中，由于数据不容易获取，测试数据极少只使用一次就丢弃。因此，实践中验证数据集和测试数据集的界限可能比较模糊。我们实际上是在使用应该被正确地称为训练数据和验证数据的数据集，并没有真正的测试数据集。

1.3 K折交叉验证

由于验证数据集不参与模型训练，当训练数据不够用时，预留大量的验证数据显得太奢侈。一种改善的方法是$k$折交叉验证（$k-fold cross-validation$）。在$k$折交叉验证中，我们把原始训练数据集分割成$k$个不重合的子数据集，然后我们做$k$次模型训练和验证。每一次，我们使用一个子数据集验证模型，并使用其他$k−1$个子数据集来训练模型。在这$k$次训练和验证中，每次用来验证模型的子数据集都不同。最后，我们对这$k$次训练误差和验证误差分别求平均。

在没有足够多的数据时使用(这是常态)
算法：
- 讲训练数据集分割成k块
- For i = 1,...,K
  - 使用第i块作为验证数据集，其余的作为训练数据集
- 报告K个验证集误差的评价
常用：K = 5 或 K = 10

总结：

训练数据集：训练模型参数
验证数据集：选择模型超参数
非大数据集上通常使用k-折交叉验证

2.过拟合和欠拟合

在深度学习和机器学习领域中，模型需同时具备良好的训练数据集适应性（体现为低训练误差）和对新，未曝光数据集的预测准确性（即强泛化能力）。泛化误差指的是模型在测试数据集上的表现，并反映了其泛化能力的强弱。而过拟合与欠拟合这两个术语，便是用以表明模型在学习与适应数据过程中可能达到的两种极端状况。过拟合指模型对训练数据的细节适应过度，以致于在新数据上表现不佳；而欠拟合则说明模型未能充分把握训练数据中的关键特征，导致无论是在训练集还是测试集上，性能都不尽人意。

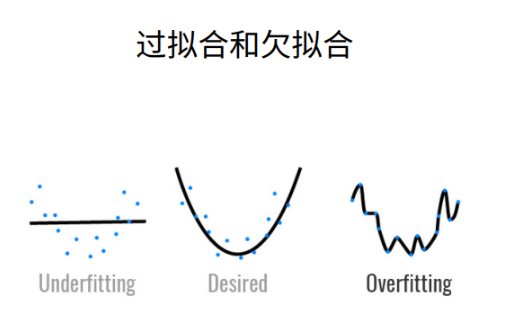
为什么会出现过拟合现象呢？

主要有以下几种情况：

训练数据集样本单一，样本不足。如果训练样本只有负样本，然后那生成的模型去预测正样本，这肯定预测不准。所以训练样本要尽可能的全面，覆盖所有的数据类型。
训练数据中噪声干扰过大。噪声指训练数据中的干扰数据。过多的干扰会导致记录了很多噪声特征，忽略了真实输入和输出之间的关系。
模型过于复杂。模型太复杂，已经能够“死记硬背”记下了训练数据的信息，但是遇到没有见过的数据的时候不能够变通，泛化能力太差。我们希望模型对不同的模型都有稳定的输出。模型太复杂是过拟合的重要因素。

下面我们来重点讨论三个因素：模型容量、模型复杂度和训练数据集大小。

2.1 模型容量

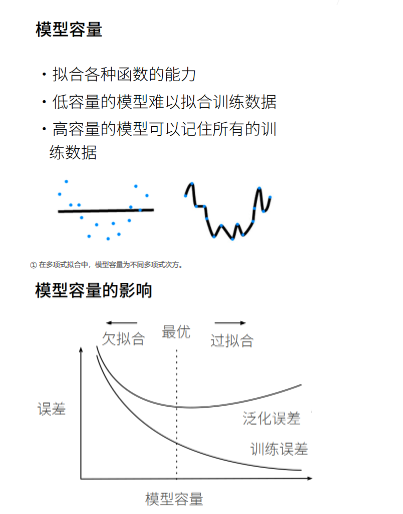
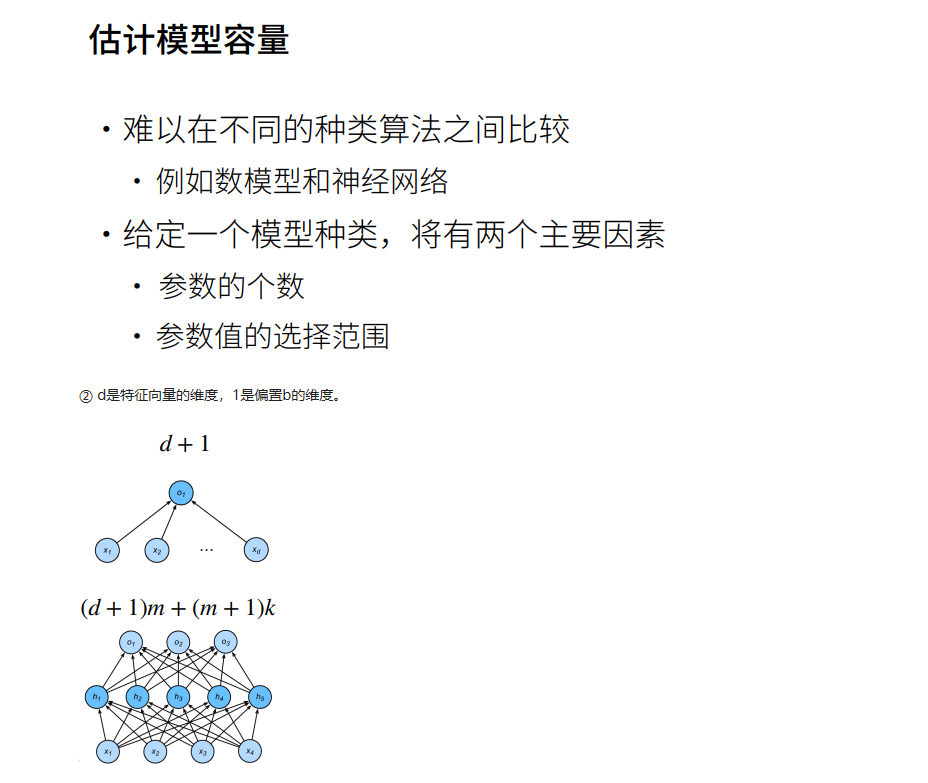
VC维

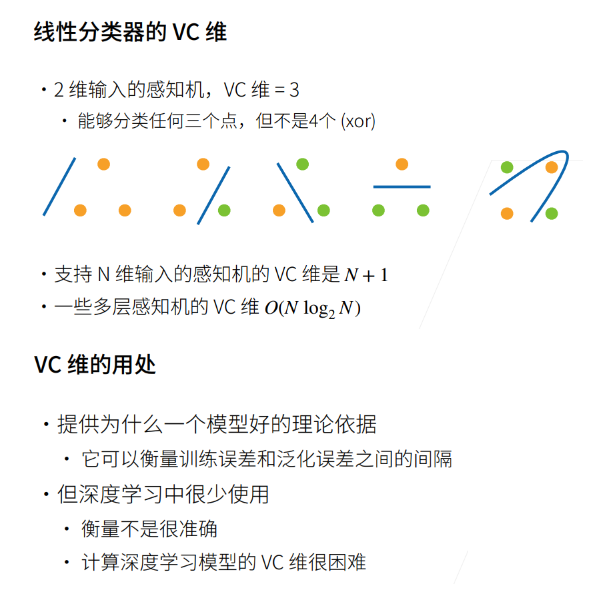
2.2模型复杂度

为了解释模型复杂度，我们以多项式函数拟合为例。给定一个由标量数据特征$x$和对应的标量标签$y$组成的训练数据集，多项式函数拟合的目标是找一个$K$阶多项式函数:

\[\hat{y} = b + \sum_{k = 1}^{K}x^kw_k \]

来近似$y$ 。

在上式中：

$w_k$是模型的权重参数
$b$是偏差参数

与线性回归相同，多项式函数拟合也使用平方损失函数。特别地，一阶多项式函数拟合又叫线性函数拟合。

模型复杂度对欠拟合和过拟合的影响：

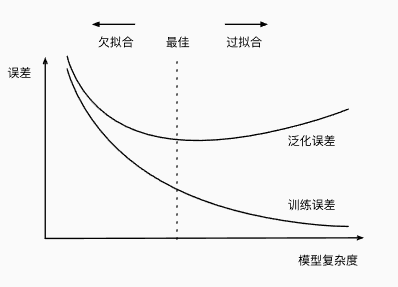
因为高阶多项式函数模型参数更多，模型函数的选择空间更大，所以高阶多项式函数比低阶多项式函数的复杂度更高。因此，高阶多项式函数比低阶多项式函数更容易在相同的训练数据集上得到更低的训练误差。

2.2训练数据集大小

影响欠拟合和过拟合的另一个重要因素是训练数据集的大小。一般来说，如果训练数据集中样本数过少，特别是比模型参数数量（按元素计）更少时，过拟合更容易发生。此外，泛化误差不会随训练数据集里样本数量增加而增大。因此，在计算资源允许的范围之内，我们通常希望训练数据集大一些，特别是在模型复杂度较高时，如层数较多的深度学习模型。

3.多项式函数拟合实验

① 使用以下三阶多项式来生成训练和测试数据的标签：

\[y = 5+1.2x-3.4\dfrac{x^2}{2!}+5.6\dfrac{x^3}{3!}+\epsilon where\epsilon \sim N(0,0.1^2) \]

② 这个式子只是一个三次多项式，并不是哪个函数的泰勒展开。

噪声项$\epsilon $服从均值为$0$且标准差为$0.1$的正态分布。在优化的过程中，我们通常希望避免非常大的梯度值或损失值。这就是我们将特征从$x^i$调整为 $\dfrac{x^i}{i!}$的原因，这样可以避免很大的$i$带来的特别大的指数值。我们将为训练集和测试集各生成100个样本。

# 通过多项式拟合来交互地探索这些概念
import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l

max_degree = 20 # 特征为20就是每一个样本是一个[20,1]的tensor
n_train, n_test = 100, 100 # 100个测试样本、100验证样本
true_w = np.zeros(max_degree)
true_w[0:4] = np.array([5,1.2,-3.4,5.6]) # 真实标号为5

features = np.random.normal(size=(n_train+n_test,1))
print(features.shape)
np.random.shuffle(features)
print(np.arange(max_degree))
print(np.arange(max_degree).reshape(1,-1))
print(np.power([[10,20]],[[1,2]]))
poly_features = np.power(features, np.arange(max_degree).reshape(1,-1)) # 对第所有维的特征取0次方、1次方、2次方...19次方  
for i in range(max_degree):
    poly_features[:,i] /= math.gamma(i+1) # i次方的特征除以(i+1)阶乘
labels = np.dot(poly_features,true_w) # 根据多项式生成y，即生成真实的labels
labels += np.random.normal(scale=0.1,size=labels.shape) # 对真实labels加噪音进去

#看一下前两个样本
true_w, features, poly_features, labels = [torch.tensor(x,dtype=torch.float32) for x in [true_w, features, poly_features, labels]]                 
print(features[:2]) # 前两个样本的x
print(poly_features[:2,:]) # 前两个样本的x的所有次方
print(labels[:2])  # 前两个样本的x对应的y

# 实现一个函数来评估模型在给定数据集上的损失
def evaluate_loss(net, data_iter, loss):
    """评估给定数据集上模型的损失"""
    metric = d2l.Accumulator(2) # 两个数的累加器
    for X, y in data_iter: # 从迭代器中拿出对应特征和标签
        out = net(X)
        y = y.reshape(out.shape) # 将真实标签改为网络输出标签的形式，统一形式
        l = loss(out, y) # 计算网络输出的预测值与真实值之间的损失差值
        metric.add(l.sum(), l.numel()) # 总量除以个数，等于平均
    return metric[0] / metric[1] # 返回数据集的平均损失

# 定义训练函数
def train(train_features, test_features, train_labels, test_labels, num_epochs=400):
    loss = nn.MSELoss()
    input_shape = train_features.shape[-1]
    net = nn.Sequential(nn.Linear(input_shape, 1, bias=False)) # 单层线性回归
    batch_size = min(10,train_labels.shape[0])
    train_iter = d2l.load_array((train_features,train_labels.reshape(-1,1)),batch_size)
    test_iter = d2l.load_array((test_features,test_labels.reshape(-1,1)),batch_size,is_train=False)    
    trainer = torch.optim.SGD(net.parameters(),lr=0.01)
    animator = d2l.Animator(xlabel='epoch',ylabel='loss',yscale='log',xlim=[1,num_epochs],ylim=[1e-3,1e2],legend=['train','test'])                   
    for epoch in range(num_epochs):
        d2l.train_epoch_ch3(net, train_iter, loss, trainer)
        if epoch == 0 or (epoch + 1) % 20 == 0:
            animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss), evaluate_loss(net,test_iter,loss)))
    print('weight',net[0].weight.data.numpy()) # 训练完后打印，打印最终学到的weight值

输出：

(200, 1)
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19]
[[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19]]
[[ 10 400]]
tensor([[-0.9840],
        [ 1.2229]])
tensor([[ 1.0000e+00, -9.8401e-01,  4.8414e-01, -1.5880e-01,  3.9065e-02,
         -7.6880e-03,  1.2608e-03, -1.7724e-04,  2.1801e-05, -2.3836e-06,
          2.3455e-07, -2.0981e-08,  1.7205e-09, -1.3023e-10,  9.1534e-12,
         -6.0047e-13,  3.6929e-14, -2.1376e-15,  1.1685e-16, -6.0519e-18],
        [ 1.0000e+00,  1.2229e+00,  7.4775e-01,  3.0481e-01,  9.3187e-02,
          2.2792e-02,  4.6454e-03,  8.1155e-04,  1.2406e-04,  1.6856e-05,
          2.0614e-06,  2.2917e-07,  2.3354e-08,  2.1969e-09,  1.9190e-10,
          1.5645e-11,  1.1958e-12,  8.6019e-14,  5.8441e-15,  3.7614e-16]])
tensor([1.1747, 5.7716])

三阶多项式函数拟合(正态)

# 三阶多项式函数拟合(正态)
train(poly_features[:n_train,:4],poly_features[n_train:,:4],labels[:n_train],labels[n_train:]) # 最后返回的weight值和公式真实weight值很接近

输出：

weight [[ 4.988501   1.2836959 -3.3589993  5.405713 ]]

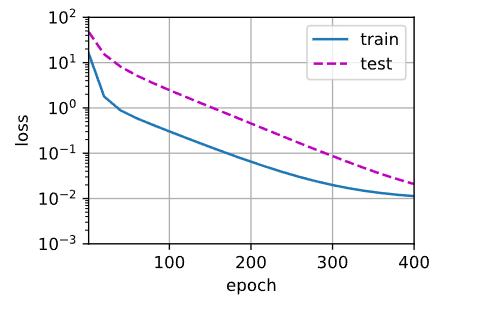
一阶多项式函数拟合(欠拟合)

# 一阶多项式函数拟合(欠拟合)
# 这里相当于用一阶多项式拟合真实的三阶多项式，欠拟合了，损失很高，根本就没降
train(poly_features[:n_train,:2],poly_features[n_train:,:2],labels[:n_train],labels[n_train:])

输出

weight [[3.6593914 3.0195978]]

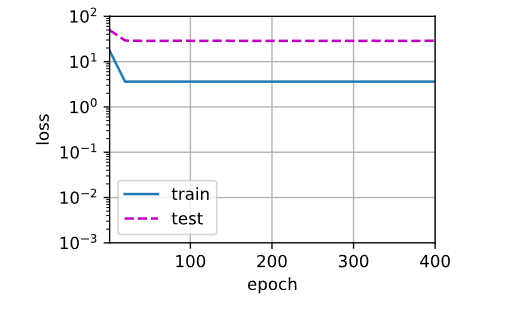
十九阶多项式函数拟合(过拟合)

# 十九阶多项式函数拟合(过拟合)
# 这里相当于用十九阶多项式拟合真实的三阶多项式，过拟合了
train(poly_features[:n_train,:],poly_features[n_train:,:],labels[:n_train],labels[n_train:])

输出：

weight [[ 4.95713     1.2931961  -3.142203    5.1588063  -0.683433    1.3676366
  -0.22168443  0.30410182  0.22201246 -0.01267278 -0.06214145 -0.1347487
  -0.16502385 -0.16112421 -0.10519557 -0.06851828  0.03842303  0.07775125
   0.12161571 -0.05093227]]

参考：https://github.com/d2l-ai/d2l-zh-pytorch-slides

posted on 2024-04-14 14:21 nannandbk 阅读(113) 评论(0) 编辑收藏举报

刷新页面返回顶部