多层感知机（MLP）
1. 单层感知机
1.1 感知机
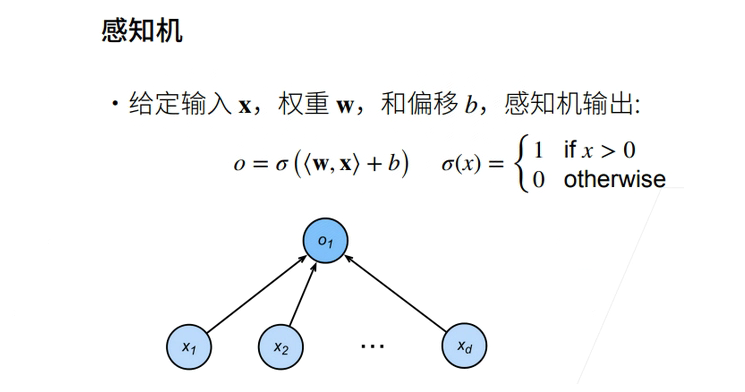
线性回归输出的是一个实数，感知机输出的是一个离散的类。
1.2 训练感知机
①如果分类正确的话y<w,x>为正数，负号后变为一个正数，和\(0\)取\(max\)之后得\(0\)，则梯度不进行更新
②如果分类错了，y<w,x>为负数，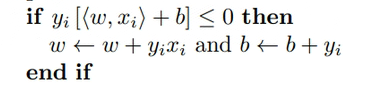
的判断条件成立，就进行梯度更新。
图示：
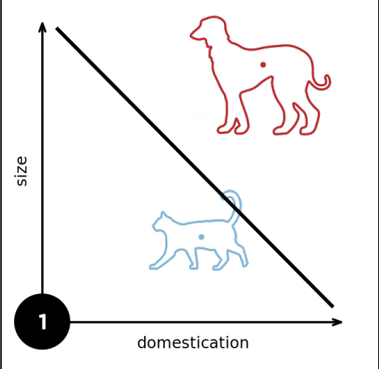
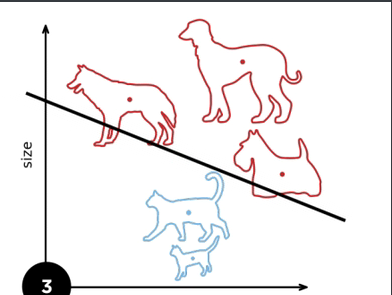
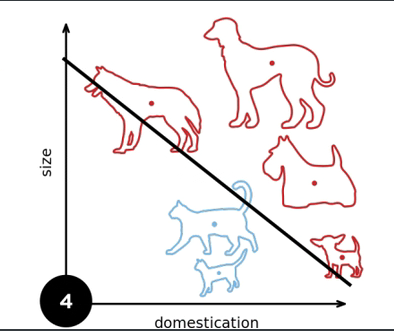
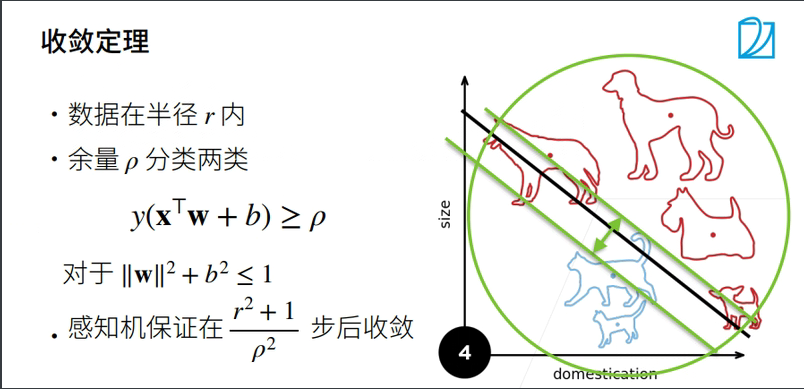
1.3 收敛半径
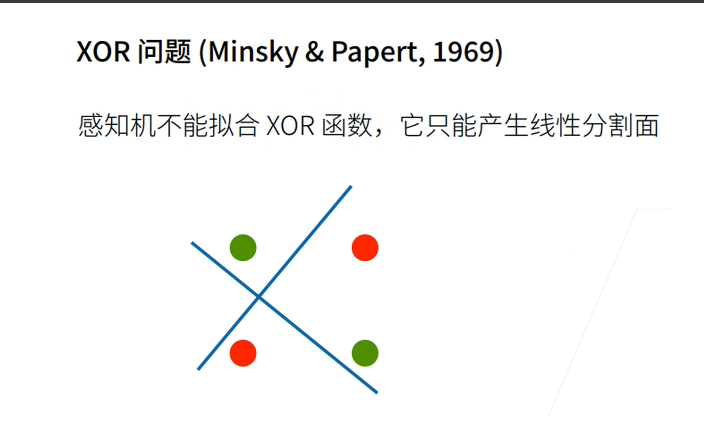
1.4 XOR问题
1.5 总结
- 感知机是一个二分类模型，是最早的AI模型之一
- 它的求解方法等价于使用批量大小为1的梯度下降
- 它不能拟合XOR函数，导致的第一次AI寒冬
2.多层感知机
2.1 学习XOR函数
我们发现单层感知机不能拟合XOR函数，那么多层行不行呢？
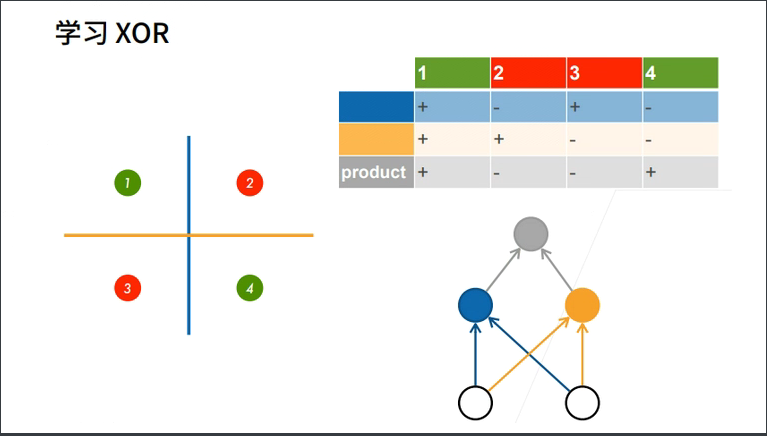
2.2 什么是多层感知机
多层感知机（MLP，Multilayer Perceptron）也叫人工神经网络（ANN，Artificial Neural Network），除了输入输出层，它中间可以有多个隐层，最简单的MLP只含一个隐层，即三层的结构，如下图：
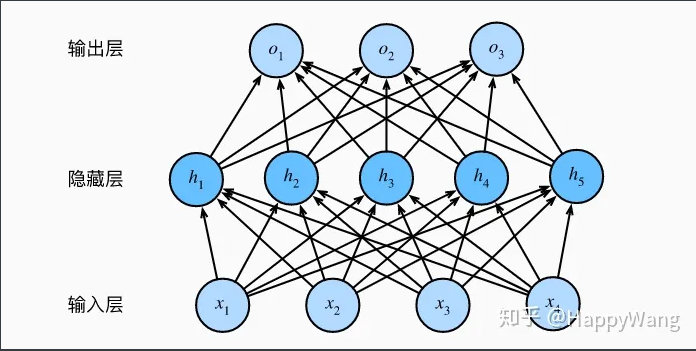
隐藏层的大小是超参数
-
输入$x \in \mathbb{R}^n $
-
隐藏层\(W_1\in \mathbb{R}^{m\times n}\),\(b_1\in\mathbb{R}^m\)
-
输出层\(w_2\in\mathbb{R}^m,b_2 \in\mathbb{R}\)
\(h = \sigma(W_1x + b_1)\)
\(o = w_2^{T}h + b_2\)
\(\sigma\)是按元素的激活函数
为什么需要非线性激活函数呢？
①不使用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合。
②使用激活函数，能够给神经元引入非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以利用到更多的非线性模型中。
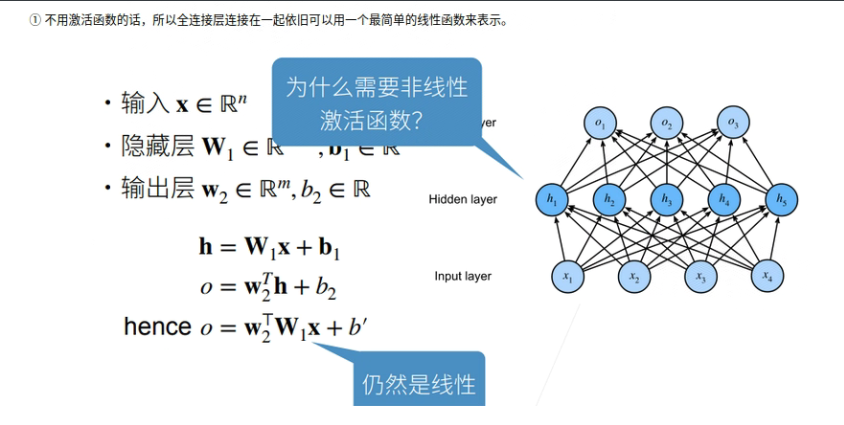
2.3 常见激活函数
激活函数需要具备以下几点性质:
- 连续并可导（允许少数点上不可导）的非线性函数。可导的激活函数可以直接利用数值优化的方法来学习网络参数。
- 激活函数及其导函数要尽可能的简单，有利于提高网络计算效率。
- 激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率和稳定性。
Sigmoid（Logistic） 函数
with autograd.record():
y = x.sigmoid()
xyplot(x, y, 'sigmoid')
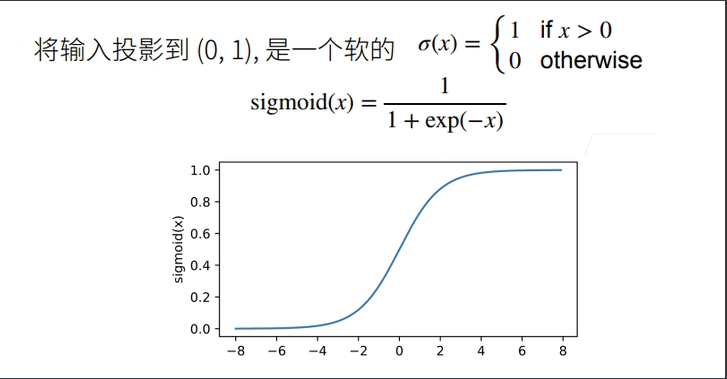
依据链式法则，sigmoid函数的导数为
\[sigmoid'(x) = sigmoid(x)(1-sigmoid(x))
\]
下面绘制了sigmoid函数的导数。当输入为0时，sigmoid函数的导数达到最大值0.25；当输入越偏离0时，sigmoid函数的导数越接近0。
y.backward()
xyplot(x, x.grad, 'grad of sigmoid')
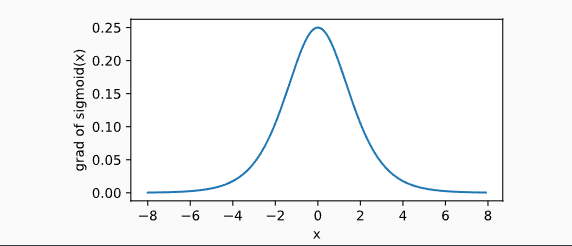
Tanh 函数
with autograd.record():
y = x.tanh()
xyplot(x, y, 'tanh')
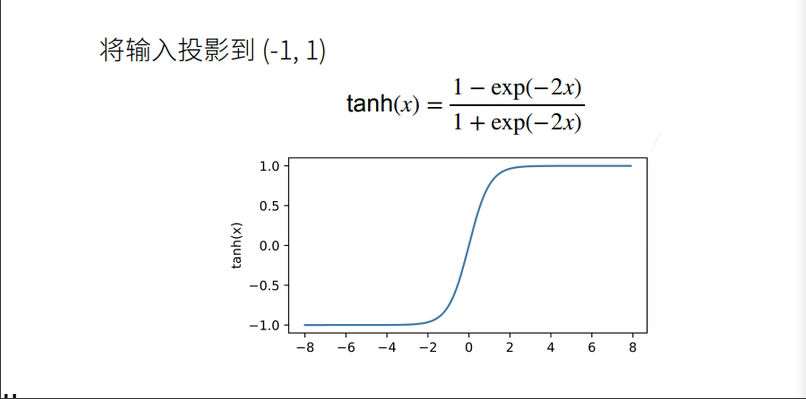
依据链式法则，tanh函数的导数为:
\[tanh'(x) = 1 - tanh^2(x)
\]
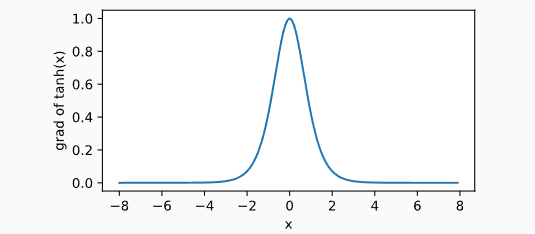
下面绘制了tanh函数的导数。当输入为0时，tanh函数的导数达到最大值1；当输入越偏离0时，tanh函数的导数越接近0。
y.backward()
xyplot(x, x.grad, 'grad of tanh')
ReLU
x = nd.arange(-8.0, 8.0, 0.1)
x.attach_grad()
with autograd.record():
y = x.relu()
xyplot(x, y, 'relu')
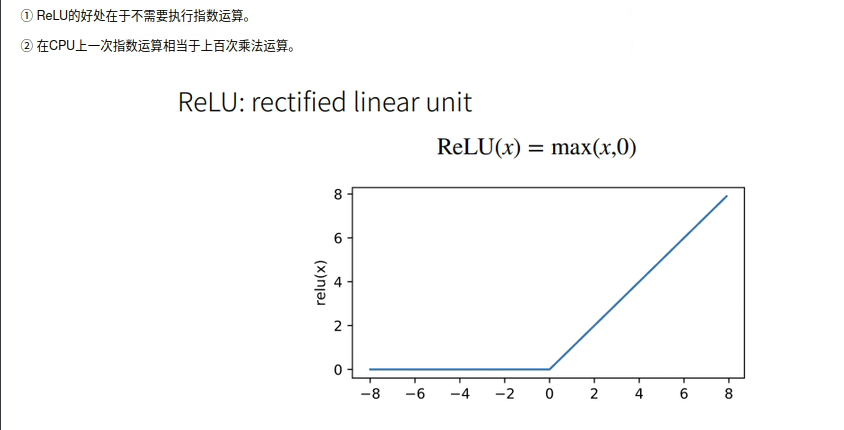
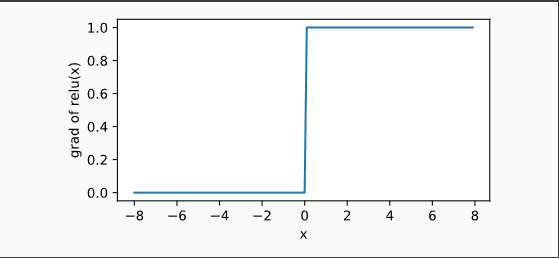
显然，当输入为负数时，ReLU函数的导数为0；当输入为正数时，ReLU函数的导数为1。尽管输入为0时ReLU函数不可导，但是我们可以取此处的导数为0。下面绘制ReLU函数的导数。
y.backward()
xyplot(x, x.grad, 'grad of relu')
2.4 多分类问题
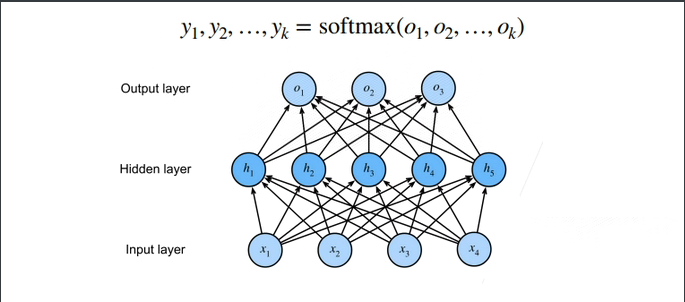
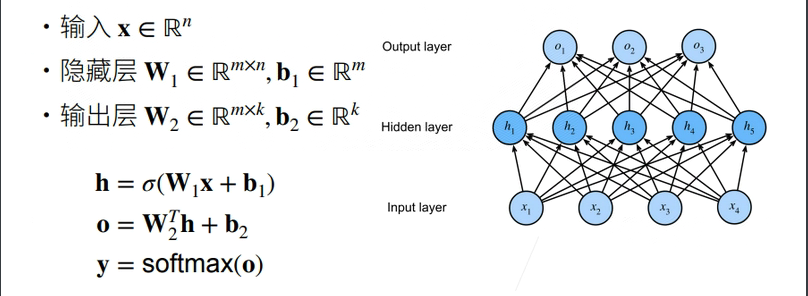
多隐藏层
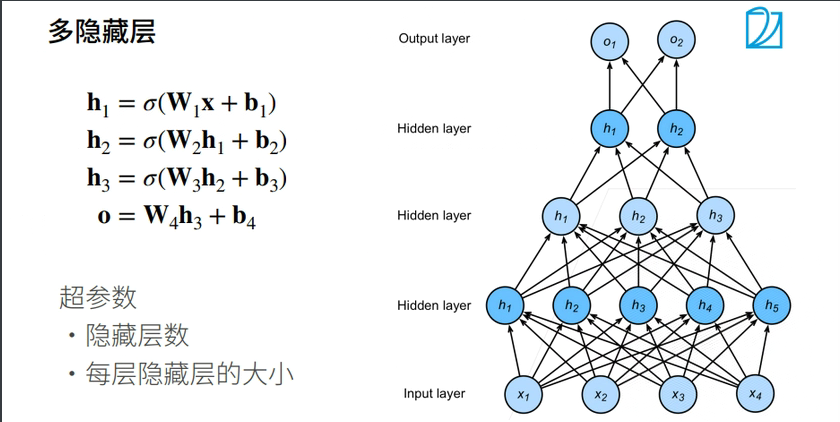
2.5 总结
- 多层感知机使用隐藏层和激活函数来得到非线性模型
- 常用激活函数是Sigmoid，Tanh，ReLU
- 使用Softmax来处理多分类问题
- 超参数为隐藏层数和各个隐藏层大小
3.多层感知机实现代码
自定义实现
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 实现一个具有单隐藏层的多层感知机，它包含256个隐藏单元
num_inputs, num_outputs, num_hiddens = 784, 10, 256 # 输入、输出是数据决定的，256是调参自己决定的
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True))
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True))
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1,b1,W2,b2]
# 实现 ReLu 激活函数
def relu(X):
a = torch.zeros_like(X) # 数据类型、形状都一样，但是值全为 0
return torch.max(X,a)
# 实现模型a
def net(X):
#print("X.shape:",X.shape)
X = X.reshape((-1, num_inputs)) # -1为自适应的批量大小
#print("X.shape:",X.shape)
H = relu(X @ W1 + b1)
#print("H.shape:",H.shape)
#print("W2.shape:",W2.shape)
return (H @ W2 + b2)
# 损失
loss = nn.CrossEntropyLoss() # 交叉熵损失
# 多层感知机的训练过程与softmax回归的训练过程完全一样
num_epochs ,lr = 30, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
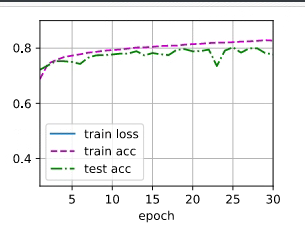
注意，这里我们把上节\(Softmax\)的代码加入到\(d2l\)里面啦。这样就可以直接调用啦。
具体方法：
pip show d2l
然后我们在相应的路径下面找到d2l的文件夹，打开后找到torch文件。打开后在最下面添加相应的函数定义即可。
train_epoch_ch3函数：
def train_epoch_ch3(net, train_iter, loss, updater): #@save
"""训练模型一个迭代周期（定义见第3章）"""
# 将模型设置为训练模式
if isinstance(net, torch.nn.Module): # isinstance()用来判断一个对象是否是一个已知的类型
net.train()
# 训练损失总和、训练准确度总和、样本数
metric = Accumulator(3)
for X, y in train_iter:
# 计算梯度并更新参数
y_hat = net(X)
l = loss(y_hat, y)
if isinstance(updater, torch.optim.Optimizer):
# 使用PyTorch内置的优化器和损失函数
updater.zero_grad()
l.mean().backward()
updater.step()
else:
# 使用定制的优化器和损失函数
l.sum().backward()
updater(X.shape[0])
metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
# 返回训练损失和训练精度
return metric[0] / metric[2], metric[1] / metric[2]
evaluate_accuracy函数：
def evaluate_accuracy(net, data_iter): #@save
"""计算在指定数据集上模型的精度"""
if isinstance(net, torch.nn.Module):
net.eval() # 将模型设置为评估模式
metric = Accumulator(2) # 正确预测数、预测总数
with torch.no_grad():
for X, y in data_iter:
metric.add(accuracy(net(X), y), y.numel())
return metric[0] / metric[1]
train_ch3函数：
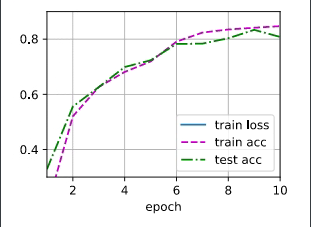
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater): #@save
#该训练函数将会运行多个迭代周期（由num_epochs指定）。 在每个迭代周期结束时，利用test_iter访问到的测试数据集对模型进行评估。
#我们将利用Animator类来可视化训练进度。
"""训练模型（定义见第3章）"""
animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
legend=['train loss', 'train acc', 'test acc'])
for epoch in range(num_epochs):
train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
test_acc = evaluate_accuracy(net, test_iter)
animator.add(epoch + 1, train_metrics + (test_acc,))
train_loss, train_acc = train_metrics
assert train_loss < 0.5, train_loss
assert train_acc <= 1 and train_acc > 0.7, train_acc
assert test_acc <= 1 and test_acc > 0.7, test_acc
框架实现
import torch
from torch import nn
from d2l import torch as d2l
# 隐藏层包含256个隐藏单元，并使用了ReLU激活函数
net = nn.Sequential(nn.Flatten(),nn.Linear(784,256),nn.ReLU(),nn.Linear(256,10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight,std=0,)
net.apply(init_weights)
# 训练过程
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
