2.6 蓝桥杯练习5题
1.[P3951 NOIP2017 提高组] 小凯的疑惑 / [蓝桥杯 2013 省] 买不到的数目
题意:小凯手中有两种面值的金币,两种面值均为正整数且彼此互素。每种金币小凯都有无数个。在不找零的情况下,仅凭这两种金币,有些物品他是无法准确支付的。现在小凯想知道在无法准确支付的物品中,最贵的价值是多少金币?
思路:数学题
不妨假设\(a<b\),答案是\(x\)。
\(x ≡ ma (\bmod b)\), \(ma + nb = x (1\le m \le b-1)\)。如果\(n>0\)的数都能表示。
那么 \(n = -1\)是第一个不合法的,此时\(x = ma-b\)。
那么: $ x_{max} = (b-1)*a-b = ab-a-b$
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
ll a,b; cin>>a>>b;
/*
设a<b,答案是x
x ≡ ma (mod b)
ma + nb = x (1<= m <= b-1)
如果n>0的数都能表示
n = -1,x = ma-b
x_max = (b-1)*a-b = ab-a-b
*/
cout<<a*b-a-b<<"\n";
return 0;
}
2.[P9232 蓝桥杯 2023 省 A] 更小的数
题意:
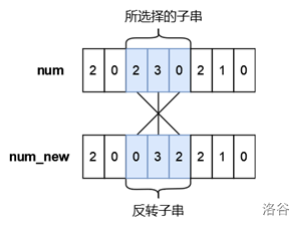
小蓝有一个长度均为 \(n\) 且仅由数字字符 \(0 \sim 9\) 组成的字符串,下标从 \(0\) 到 \(n-1\),你可以将其视作是一个具有 \(n\) 位的十进制数字 \(num\),小蓝可以从 \(num\) 中选出一段连续的子串并将子串进行反转,最多反转一次。小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字 \(num_{new}\) 满足条件 \(num_{new}<num\),请你帮他计算下一共有多少种不同的子串选择方案,只要两个子串在 \(num\) 中的位置不完全相同我们就视作是不同的方案。
注意,我们允许前导零的存在,即数字的最高位可以是 \(0\),这是合法的。
思路:区间\(dp\)。
我们从后往前做,\(dp[i][j]\)表示\(翻转i到j这一段是否合法\)。
很显然对于\(s[i]>s[j]\)的情况,\(dp[i][j] = 1\)。
那么对于\(s[i]=s[j]\)的情况,\(dp[i][j] = dp[i+1][j-1]\)(向内缩小一个,这也是为什么我们倒着做原因)。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 5e3 + 10;
string s;
int n;
bool dp[N][N];
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
cin>>s;
n = s.size();
s = "?" + s;
int cnt = 0;
for(int i = n;i >= 1; i--)
{
for(int j = i;j <= n; j++)
{
if(s[i] > s[j]) dp[i][j] = true;
else if(s[i] == s[j])dp[i][j] = dp[i+1][j-1];
if(dp[i][j])cnt++;
}
}
cout<<cnt<<"\n";
return 0;
}
3.[P8667 [蓝桥杯 2018 省 B] 递增三元组
题意:给定三个整数数组 \(A = [A_1, A_2,\cdots, A_N]\),\(B = [B_1, B_2,\cdots, B_N]\),\(C = [C_1, C_2,\cdots,C_N]\)。
请你统计有多少个三元组 \((i, j, k)\) 满足:
- \(1 \le i, j, k \le N\)
- \(A_i < B_j < C_k\)
思路:排序+二分。枚举\(b_i\),看看对于当前的\(b_i\)有多少个合法的\(a_i\)和\(c_i\),然后组合一下。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
ll a[N],b[N],c[N];
bool cmp(int a,int b)
{
return a>b;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int n; cin>>n;
for(int i = 1;i <= n; i++)
cin>>a[i];
for(int i = 1;i <= n; i++)
cin>>b[i];
for(int i = 1;i <= n; i++)
cin>>c[i];
sort(a+1,a+1+n);
sort(c+1,c+1+n,cmp);
ll ans = 0;
for(int i = 1;i <= n; i++)
{
int x = b[i];
int l = 1,r = n;
ll t1,t2;
while(l<=r)
{
int mid = (l+r)>>1;
if(a[mid]<x)l = mid+1;
else r = mid-1;
}
t1 = l-1;
//cout<<"t1 = "<<t1<<"\n";
l = 1,r = n;
while(l<=r)
{
int mid = (l+r)>>1;
if(c[mid]>x)l = mid+1;
else r = mid-1;
}
t2 = l-1;
//cout<<"t2 = "<<t2<<"\n";
ans += t1*t2;
}
cout<<ans<<"\n";
return 0;
}
4.[P8602 [蓝桥杯 2013 省 A] 大臣的旅费
题意:很久以前,T 王国空前繁荣。为了更好地管理国家,王国修建了大量的快速路,用于连接首都和王国内的各大城市。
为节省经费,T 国的大臣们经过思考,制定了一套优秀的修建方案,使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。同时,如果不重复经过大城市,从首都到达每个大城市的方案都是唯一的。
J 是 T 国重要大臣,他巡查于各大城市之间,体察民情。所以,从一个城市马不停蹄地到另一个城市成了 J 最常做的事情。他有一个钱袋,用于存放往来城市间的路费。
聪明的 J 发现,如果不在某个城市停下来修整,在连续行进过程中,他所花的路费与他已走过的距离有关,在走第 \(x\) 千米到第 \(x+1\) 千米这一千米中(\(x\) 是整数),他花费的路费是 \(x+10\) 这么多。也就是说走 \(1\) 千米花费 \(11\),走 \(2\) 千米要花费 \(23\)。
J 大臣想知道:他从某一个城市出发,中间不休息,到达另一个城市,所有可能花费的路费中最多是多少呢?
思路:树上\(dp\)。
本题的关键是什么呢?读完题我就感觉奇怪,为什么要特别提出:使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。同时,如果不重复经过大城市,从首都到达每个大城市的方案都是唯一的。
方案是唯一的,说明它没有环。那么不就是一棵树吗?那就好做了。
我们处理出以\(u\)为根它子树\(v\)里面里面的最长和次长的两条路。答案就是以某个点为根,次长+最长最大的那个。那么接下来处理答案。
题目说:在走第 \(x\) 千米到第 \(x+1\) 千米这一千米中(\(x\) 是整数),他花费的路费是 \(x+10\) 这么多。也就是说走 \(1\) 千米花费 \(11\),走 \(2\) 千米要花费 \(23\)。
我们发现是个等差数列,那么\(O(1)\)处理一下就行了。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
int n,m;
vector<array<int,2>>e[N];
ll dist[N];
struct node
{
ll fi,se;
}f[N];
ll get(ll l,ll r)
{
return (l+r)*(r-l+1)/2;
}
void dfs(int u,int fa)
{
ll fi = 0,se = 0;
for(auto [v,d] : e[u])
{
if(v == fa)continue;
dfs(v,u);
}
for(auto [v,d] : e[u])
{
if(v == fa)continue;
ll t = d + f[v].fi;
if(t > fi) se = fi,fi = t;
else se = max(se,t);
}
f[u].fi = fi,f[u].se = se;
// cout<<"u = "<<u<<" f[u].fi = "<<f[u].fi<<" f[u].se = "<<f[u].se<<"\n";
}
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
cin>>n; m = n-1;
for(int i = 1;i <= m; i++)
{
int u,v,d; cin>>u>>v>>d;
e[u].push_back({v,d});
e[v].push_back({u,d});
}
dfs(1,0);
ll mx = 0;
for(int i = 1;i <= n; i++)
mx = max(mx,f[i].se + f[i].fi);
ll ans = get(11,11+mx-1);
//cout<<"mx = "<<mx<<"\n";
cout<<ans<<"\n";
return 0;
}
5.[P8614 [蓝桥杯 2014 省 A] 波动数列
题意:观察这个数列:
$1,3,0,2,-1,1,-2, \cdots $。
这个数列中后一项总是比前一项增加 \(2\) 或者减少 \(3\)。
栋栋对这种数列很好奇,他想知道长度为 \(n\) 和为 \(s\) 而且后一项总是比前一项增加 \(a\) 或者减少 \(b\) 的整数数列可能有多少种呢?
思路:这题挺难的TAT
这个数据范围,感觉是\(dp\)啊。可是不知道怎么\(dp\)?可能是数学题。
\(a_i = a_{i-1}+a\)或者\(a = a_{i-1}-b\),我们令\(P = +a或-b\)。那么则有\(a_i = a_{i-1}+P\)
又因为\(s = \sum_{i = 1}^{n}a_i = a_1+a_2+...+a_n = a_1+(a_1+P)+(a_1+2P)+(a_1+3P)+...+(a_1+(n-1)P)\)
即\(s = na_1 + \dfrac{n(n-1)}{2}P\),我们令\(z =\dfrac{n(n-1)}{2}P\)
那么\(a_1 = \dfrac{s-z}{n}\),又因为\(a_1\)是整数,那么\((s-z)\%n=0\),即\(s-z≡0(\bmod n)\),即\(s≡z(\bmod n)\)
也就是说\(s\)和\(z\)是同余的。那么可以开始考虑如何\(dp\)啦。
\(dp[i][j]\)表示,考虑前\(i\)个\(P\),余数是\(j\)的种数。
\(dp[i][j] = dp[i-1][((j-i*a)\%n+n)\%n\)\(]\)+$ dp[i-1][((j+i*b)%n+n)%n$$]$
答案就是\(dp[n-1][(s\%n+n)\%n]%mod\)(因为只有\(n-1\)个\(P\))
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e8 + 7;
const int N = 2e3 + 10;
ll dp[N][N],n,s,a,b;
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
cin>>n>>s>>a>>b;
dp[0][0] = 1;
for(int i = 1;i <= n-1; i++)
{
for(int j = 0;j < n; j++)
{
dp[i][j] = dp[i-1][((j-i*a)%n+n)%n]+dp[i-1][((j+i*b)%n+n)%n];
dp[i][j] %= mod;
}
}
cout<<dp[n-1][(s%n+n)%n]%mod<<"\n";
return 0;
}





