2.1 蓝桥杯练习5题
1.[P8623 蓝桥杯 2015 省 B] 移动距离
题意:X 星球居民小区的楼房全是一样的,并且按矩阵样式排列。其楼房的编号为 $1,2,3, \cdots $ 。
当排满一行时,从下一行相邻的楼往反方向排号。
比如:当小区排号宽度为 \(6\) 时,开始情形如下:
1 2 3 4 5 6
12 11 10 9 8 7
13 14 15 .....
我们的问题是:已知了两个楼号 \(m\) 和 \(n\),需要求出它们之间的最短移动距离。(不能斜线方向移动)
思路:这让我想到了二维坐标压缩到一维的那个操作。这里其实就是展开。还要注意的就是偶数行是倒着来的。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int w,m,n; cin>>w>>m>>n;
int x1 = (m-1) / w ,y1 = m % w;
int x2 = (n-1) / w ,y2 = n % w;
// cout<<"("<<x1<<","<<y1<<")"<<"\n";
// cout<<"("<<x2<<","<<y2<<")"<<"\n";
if(x1 % 2 == 0)y1 = w - y1 + 1;
if(x2 % 2 == 0)y2 = w - y2 + 1;
// cout<<"("<<x1<<","<<y1<<")"<<"\n";
// cout<<"("<<x2<<","<<y2<<")"<<"\n";
int ans = abs(x1-x2)+abs(y1-y2);
cout<<ans<<"\n";
return 0;
}
2.[P8651 蓝桥杯 2017 省 B] 日期问题
题意:小明正在整理一批历史文献。这些历史文献中出现了很多日期。小明知道这些日期都在 1960 年 1 月 1 日至 2059 年 12 月 31 日。令小明头疼的是,这些日期采用的格式非常不统一,有采用年/月/日的,有采用月/日/年的,还有采用日/月/年的。更加麻烦的是,年份也都省略了前两位,使得文献上的一个日期,存在很多可能的日期与其对应。
比如 02/03/04,可能是 2002 年 03 月 04 日、2004 年 02 月 03 日或 2004 年 03 月 02 日。
给出一个文献上的日期,你能帮助小明判断有哪些可能的日期对其对应吗?
思路:给的格式是AA/BB/CC,那么可以操作的只有前面年份。两种选择加\(19\)或者加\(20\)。弄完之后看年份在不在范围内,之后根据平闰年规则看月和日合不合法即可。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
bool check(int y,int m,int d){
if(d<=0)return 0;//特判
if(m==1||m==3||m==5||m==7||m==8||m==10||m==12){//大月
if(d<=31)return 1;
}
if(m==4||m==6||m==9||m==11){//小月
if(d<=30)return 1;
}
if(m==2){//二月
if(y%4==0){//闰年
if(d<=29)return 1;
}else{//平年
if(d<=28)return 1;
}
}
return 0;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
string s; cin>>s;
string a = s.substr(0,2);
string b = s.substr(3,2);
string c = s.substr(6,2);
set<string>st;
//年月日
string op1 = "19",op2 = "20";
string y1 = op1 + a;
int yy1 = stoi(y1);
if(1960<=yy1&&yy1<=2059 && check(yy1,stoi(b),stoi(c)))
st.insert(y1+"-"+b+"-"+c);
y1 = op2 + a;
yy1 = stoi(y1);
if(1960<=yy1&&yy1<=2059 && check(yy1,stoi(b),stoi(c)))
st.insert(y1+"-"+b+"-"+c);
//月日年
y1 = op1 + c;
yy1 = stoi(y1);
if(1960<=yy1&&yy1<=2059 && check(yy1,stoi(a),stoi(b)))
st.insert(y1+"-"+a+"-"+b);
y1 = op2 + c;
yy1 = stoi(y1);
if(1960<=yy1&&yy1<=2059 && check(yy1,stoi(a),stoi(b)))
st.insert(y1+"-"+a+"-"+b);
//日月年
y1 = op1 + c;
yy1 = stoi(y1);
if(1960<=yy1&&yy1<=2059 && check(yy1,stoi(b),stoi(a)))
st.insert(y1+"-"+b+"-"+a);
y1 = op2 + c;
yy1 = stoi(y1);
if(1960<=yy1&&yy1<=2059 && check(yy1,stoi(b),stoi(a)))
st.insert(y1+"-"+b+"-"+a);
for(auto x : st)
cout<<x<<"\n";
return 0;
}
3.[P8637 蓝桥杯 2016 省 B] 交换瓶子
题意:有 \(N\) 个瓶子,编号 \(1 \sim N\),放在架子上。
比如有 \(5\) 个瓶子:
要求每次拿起 \(2\) 个瓶子,交换它们的位置。
经过若干次后,使得瓶子的序号为:
对于这么简单的情况,显然,至少需要交换 \(2\) 次就可以复位。
如果瓶子更多呢?你可以通过编程来解决。
思路:如果当前的瓶子不在该在的位置上,那么我们就把他放在他应该在的位置。如果原本就已经在了,就跳过他。因为每一个数都有一个属于自己的最终位置,所以我们让每一个数换到它最终的位置之后,他就不用再动了。也就是每个数换一次。这样的话时间复杂度是\(O(n)\)的。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
int a[N],id[N];
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int n; cin>>n;
for(int i = 1;i <= n; i++)
{
cin>>a[i];
}
int cnt = 0;
for(int i = 1;i <= n; i++)
{
if(a[i] != i)
{
cnt++;
for(int j = i+1; j <= n; j++)if(a[j] == i){
swap(a[i],a[j]);
}
}
}
cout<<cnt<<"\n";
return 0;
}
法二:学习的别人的做法,可以把有关系的点进行连边,因为它存在拓扑关系。之后会形成环,答案就是n-环数。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
bool vis[N];
int n,a[N],cnt;
vector<int>e[N];
void dfs(int u,int fa)
{
// cout<<"u = "<<u<<"\n";
if(vis[u])return;
vis[u] = true;
for(auto v : e[u])
{
if(v == fa)continue;
dfs(v,u);
}
}
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
cin>>n;
for(int i = 1;i <= n; i++)
{
cin>>a[i];
if(a[i] != i){
e[a[i]].push_back(i);
e[i].push_back(a[i]);
}
}
for(int i = 1;i <= n; i++)
{
if(!vis[i])
{
dfs(i,0);
cnt++;
}
}
cout<<n-cnt<<"\n";
return 0;
}
4.交换瓶子的拓展题——P1327 数列排序
题意:给定一个数列 \(a\),这个数列满足 \(a_i \not =a_j\)(\(i\not=j\)),现在要求你把这个数列从小到大排序,每次允许你交换其中任意一对数,请问最少需要几次交换?
思路:其实和上一题很类似,几乎就一样,但是现在包含负数,数据范围到达了\(1e5\)。
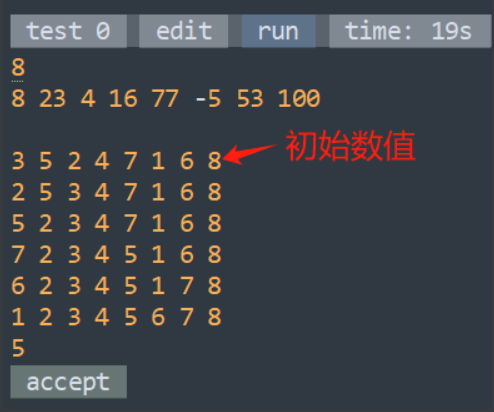
我们可以把记录原数的数值和位置,我们可以把原数的位置看成他们新的数值\(a[i].id\),这样解决了有负数的情况。然后按照数值大小排序,用\(s\)数组记录每个数应该在的位置。然后和上一题类似的,如果它不在自己的位置,我们把当前的数放到他应该放到的位置,直到当前位置对的。因为每一个数都有一个属于自己的最终位置,所以我们让每一个数换到它最终的位置之后,他就不用再动了。也就是每个数换一次。这样的话时间复杂度是\(O(n)\)的。
以样例为例,s数组的情况:
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
struct node
{
int val,id;
}a[N];
int s[N];
bool cmp(node a, node b)
{
return a.val<b.val;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int n; cin>>n;
for(int i = 1;i <= n; i++)
cin>>a[i].val,a[i].id = i;
sort(a+1,a+1+n,cmp);
for(int i = 1;i <= n; i++)
s[a[i].id] = i;
// for(int i = 1;i <= n; i++)
// cout<<s[i]<<" ";
// cout<<"\n";
int cnt = 0;
for(int i = 1;i <= n; i++)
{
while(s[i] != i)
{
swap(s[i],s[s[i]]);
cnt++;
// for(int i = 1;i <= n; i++)
// cout<<s[i]<<" ";
// cout<<"\n";
}
}
cout<<cnt<<"\n";
return 0;
}
其实上面这两个题我一开始想到的是会不会和逆序对有关,但是不对,逆序对是只允许交换相邻两个数,而上面的题没有要求。如果只能交换相邻的,我们可以考虑逆序对的做法。
5.P1908 逆序对
思路:用树状数组,注意要处理有相同数的情况!
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e5+10;
int n;
struct node
{
int val,id;
}a[N];
int s[N];
bool cmp(node a, node b)
{
if(a.val == b.val)
return a.id < b.id;
return a.val < b.val;
}//!注意相等的情况的处理
ll c[N];
ll query(int x){//1...x
ll s = 0;
for(;x;x-=x&(-x))
s += c[x];
return s;
}
void modify(int x,ll s){//a[x]+=s
for(;x<=n;x+=x&(-x))
c[x]+=s;
}
signed main()
{
cin>>n;
for(int i = 1;i<=n;i++)
{
cin>>a[i].val;
a[i].id = i;
}
sort(a+1,a+1+n,cmp);
for(int i = 1;i <= n; i++)
s[a[i].id] = n + 1 - i;
ll ans = 0;
for(int i = 1;i <= n; i++)
ans += query(s[i]),modify(s[i],1);
cout<<ans<<endl;
return 0;
}





