1.31 蓝桥杯练习5题
退役哩,但是下学期还要打蓝桥。好久没写题脑袋空空,准备每天写几个练手。
1.[P8599 蓝桥杯 2013 省 B] 带分数
题意:\(100\) 可以表示为带分数的形式:\(100 = 3 + \frac{69258}{714}\)。
还可以表示为:\(100 = 82 + \frac{3546}{197}\)。
注意特征:带分数中,数字 \(1\) ~ \(9\) 分别出现且只出现一次(不包含 \(0\))。
类似这样的带分数,\(100\) 有 \(11\) 种表示法。
思路:解题的关键在于数字 \(1\) ~ \(9\) 分别出现且只出现一次。那么对于一个带分数,我们可以分成三个部分:整数,分子,分母。由于题目给的时限是3秒,可以进行9的全排列,然后把这个排列分成3份,看可行性即可。
注意,对于除法不好判断,可以转化为乘法。
因为\(a+\dfrac{b}{c} = n\)则当\((n-a)*c = b\)成立时候是合法的。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
int n,num[]={0,1,2,3,4,5,6,7,8,9};
int get(int l,int r)
{
int res = 0;
for(int i = l; i <= r; i++)
{
res *= 10;
res += num[i];
}
return res;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
cin>>n;
int ans = 0;
do{
for(int i = 1;i <= 7; i++)
{
for(int j = i+1;j <= 8; j++)
{
int a = get(1,i),b = get(i+1,j),c = get(j+1,9);
if((n-a)*c==b){
// cout<<"a = "<<a<<" b = "<<b<<" c = "<<c<<"\n";
ans++;
}
}
}
}while(next_permutation(num+1,num+10));
cout<<ans<<"\n";
return 0;
}
2.[P8787 蓝桥杯 2022 省 B] 砍竹子
题意:这天,小明在砍竹子,他面前有 \(n\) 棵竹子排成一排,一开始第 \(i\) 棵竹子的高度为 \(h_{i}\).
他觉得一棵一棵砍太慢了,决定使用魔法来砍竹子。魔法可以对连续的一段相同高度的竹子使用,假设这一段竹子的高度为 \(H\),那么使用一次魔法可以把这一段竹子的高度都变为 \(\left\lfloor\sqrt{\left\lfloor\frac{H}{2}\right\rfloor+1}\right\rfloor\), 其中 \(\lfloor x\rfloor\) 表示对 \(x\) 向下取整。小明想知道他最少使用多少次魔法可以让所有的竹子的高度都变为 \(1\)。
思路:思考怎样才能使用魔法次数尽量的少,那就是在变到1之前连续一样的数尽可能的多。那么我们可以先预处理出每一个竹子高度变为1所要的操作次数。我们考虑贪心的去砍,因为我们想要连续的一样的尽量的多,并且我们不能使得矮的变成高的,那么我们肯定是优先砍高的,其他的不会更优。
具体操作:先预处理出每棵竹子需要砍的次数,从高到低去砍,注意如果当前的和下一个是一样的操作次数,但是注意如果高度不一样我们还是不能一起使用魔法的,只能对它(和它之前一样高度的)单独用。如果一样的话就可以和后面的一起使用魔法(注意我们是找到第一个不连续的那个进行统计的)。具体细节看代码
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
ll a[N],b[N],mx;
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
ll n; cin>>n;
for(int i = 1;i <= n; i++)
cin>>a[i];
for(int i = 1;i <= n; i++)
{
ll cnt = 0;
ll t = a[i];
while(t != 1)
{
cnt++;
t = sqrt(t/2+1);
}
b[i] = cnt;
mx = max(mx,b[i]);
}
ll cnt = 0;
for(int i = mx;i > 0;i--)
{
for(int j = 1;j <= n; j++)
{
if(b[j] == i)
{
if(a[j] != a[j+1]) cnt++;//和后一个不一样,说明不可能有更多的连续的,需要用魔法
b[j]--;//砍过一次了,操作次数-1
a[j] = sqrt(a[j]/2+1);//高度变化
}
}
}
cout<<cnt<<"\n";
return 0;
}
3.[P8597 蓝桥杯 2013 省 B] 翻硬币
题意:桌上放着排成一排的若干硬币。我们用 * 表示正面,用 o 表示反面(是小写字母,不是零),比如可能情形是 **oo***oooo,如果同时翻转左边的两个硬币,则变为 oooo***oooo。现在小明的问题是:如果已知了初始状态和要达到的目标状态,每次只能同时翻转相邻的两个硬币,那么对特定的局面,最少要翻动多少次呢?
思路:这个题很简单啦,直接模拟就行了,因为题目说一定有解,那么需要翻动我就一定要翻。从前往后翻,同一组之后翻一次,这样是最优的。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
string s,t; cin>>s>>t;
s = "?" + s;
t = "?" + t;
int n = s.size(),cnt = 0;
for(int i = 1;i < n; i++)
{
if(s[i] != t[i])
{
cnt++;
s[i] = t[i];
if(s[i+1]=='*')s[i+1] = 'o';
else s[i+1] = '*';
}
}
cout<<cnt<<"\n";
return 0;
}
4.[P9242 蓝桥杯 2023 省 B] 接龙数列
题意:对于一个长度为 \(K\) 的整数数列:\(A_{1},A_{2},\ldots,A_{K}\),我们称之为接龙数列当且仅当 \(A_{i}\) 的首位数字恰好等于 \(A_{i-1}\) 的末位数字(\(2 \leq i \leq K\))。
例如 \(12,23,35,56,61,11\) 是接龙数列;\(12,23,34,56\) 不是接龙数列,因为 \(56\) 的首位数字不等于 \(34\) 的末位数字。所有长度为 \(1\) 的整数数列都是接龙数列。
现在给定一个长度为 \(N\) 的数列 \(A_{1},A_{2},\ldots,A_{N}\),请你计算最少从中删除多少 个数,可以使剩下的序列是接龙序列?
思路:一开始我不知道怎么去写,最少次数,感觉可能是二分?但是check函数写不了啊。看到数据范围\(1e5\),可能是\(O(N)\)的,总共就\(9\)个数字,那么考虑\(dp[i]\)表示以\(i\)结尾最多能接上多少个?答案就是\(min(n-dp[1~9])\)
转移方程怎么写嘞?因为我们只用考虑首尾就行了,假设当前的首是\(s\),尾是\(e\)。
考虑当前这个要还是不要,如果要接在前面,那么前一个的尾要是\(s\),接上了的话答案就是\(dp[s]+1\)。如果不要这个就是直接继承\(dp[e]\)即可。
于是\(dp[e] = max(dp[e],dp[s]+1)\)
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 1e5 + 10;
ll dp[N];
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int n; cin>>n;
for(int i = 1;i <= n; i++)
{
string s; cin>>s;
int len = s.size();
dp[s[len-1]-'0'] = max(dp[s[len-1]-'0'],dp[s[0]-'0']+1);
}
ll ans = 0;
for(int i = 0;i <= 9; i++)
ans = max(ans,dp[i]);
cout<<n-ans<<"\n";
return 0;
}
5.[P8784 蓝桥杯 2022 省 B] 积木画
题意:小明最近迷上了积木画,有这么两种类型的积木,分别为 \(I\) 型(大小为 \(2\) 个单位面积) 和 \(L\) 型 (大小为 \(3\) 个单位面积):
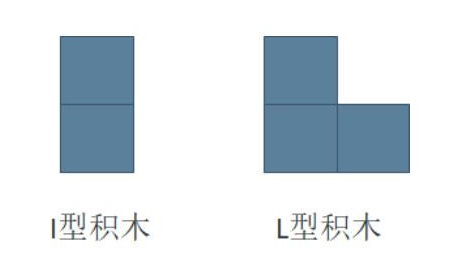
同时,小明有一块面积大小为 \(2 \times N\) 的画布,画布由 \(2 \times N\) 个 \(1 \times 1\) 区域构成。小明需要用以上两种积木将画布拼满,他想知道总共有多少种不同的方式? 积木可以任意旋转,且画布的方向固定。
思路:这个题是个图形\(dp\),统计方案数。我们一步步来考虑。
\(2\times n\)的地方放积木,问方案数,考虑怎么放感觉会很困难,我们考虑最后一步要怎么放是不是容易很多呢?
冬天手冷,字略丑QAQ..hh
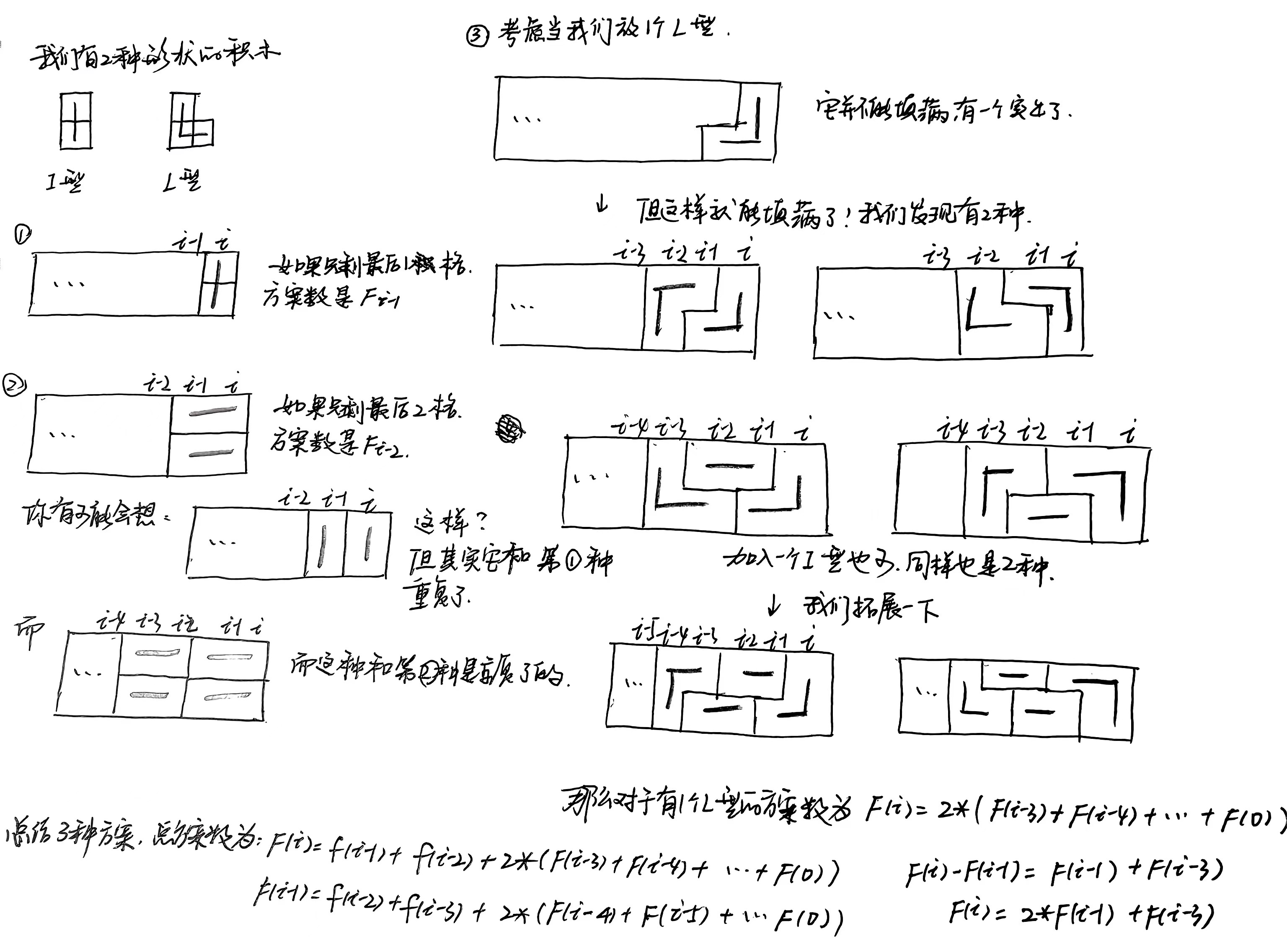
综上所述:答案就是:\(F[i] = 2*F[i-1]+F[i-3]\)
其中:\(F[1] = 1,F[2] = 2,F[3] = 5\)
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e7 + 10;
ll f[N];
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int n; cin>>n;
f[1] = 1,f[2] = 2,f[3] = 5;
for(int i = 4;i <= n; i++)
{
f[i] = (2*f[i-1]%mod+f[i-3])%mod;
}
cout<<f[n]<<"\n";
return 0;
}



