关于旋转矩阵

关于旋转矩阵

1.将矩阵旋转90°

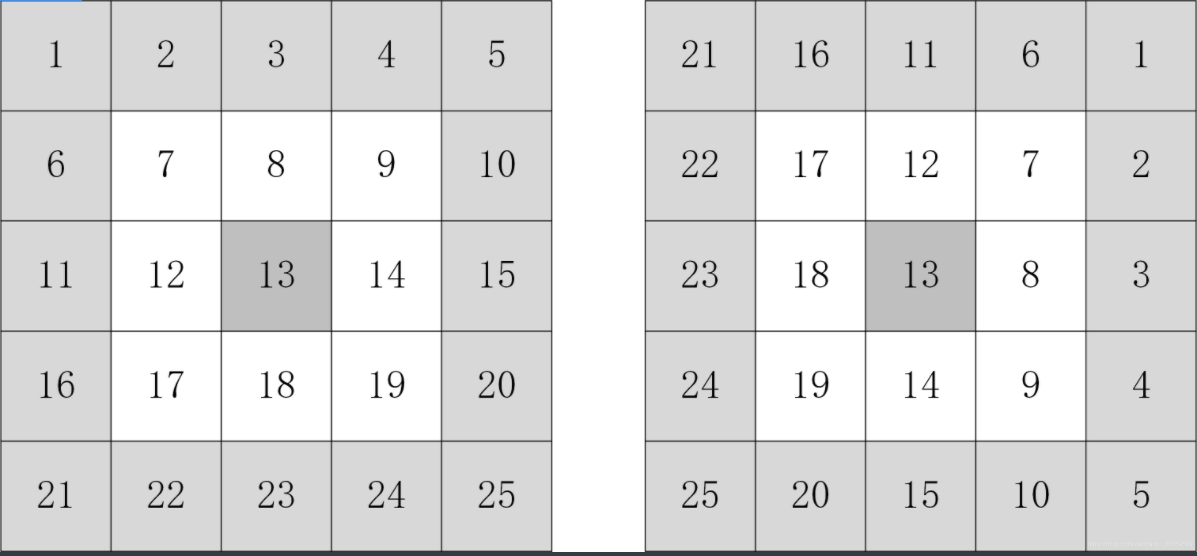
分析：对于\(N\)阶方阵，如果\(N\)是偶数那么矩阵构成\(N/2\)圈；如果\(N\)是奇数，则矩阵构成\((N-1)/2\)圈。

将矩阵顺时针旋转90°，就是没券的元素在四个方位依次轮换位置。

那么，交换元素公式就是：

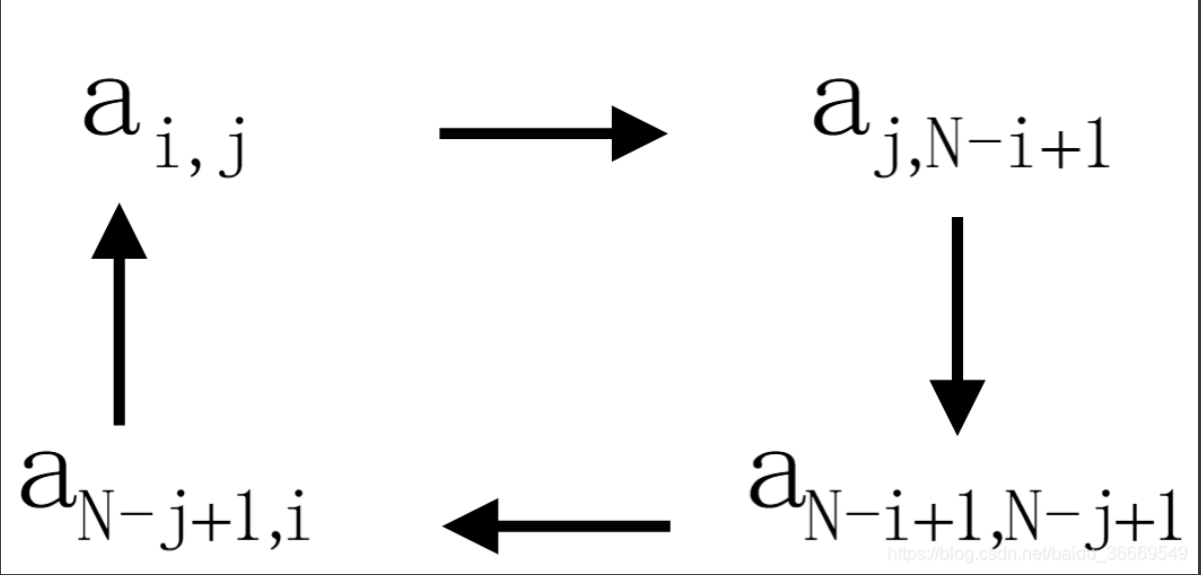
例题：C. Perfect Square

// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
char s[1010][1010];
int main()
{
    ios::sync_with_stdio(false);   cin.tie(nullptr), cout.tie(nullptr);
    int t; cin>>t;
    while(t--)
    {
        int n; cin>>n;
        for(int i = 1;i <= n; i++)
            for(int j = 1;j <= n; j++)
                cin>>s[i][j];
        ll ans = 0;
        int m = n/2;
        /*
            a[i][j] -> a[j][N-i+1]
             ↓             ↑
            a[N-j+1][i]<-a[N-i+1][N-j+1]
        */
        for(int i = 1;i <= m; i++)
        {
            for(int j = i; j < n-i+1; j++)
            {
                char a[4] = {s[i][j],s[j][n-i+1],s[n-i+1][n-j+1], s[n-j+1][i]};
                char mx = a[0];

                for(int k = 1;k < 4; k++)
                    mx = max(mx,a[k]);
                for(int k = 0;k < 4; k++)
                    ans += mx-a[k];
            }
        }
        cout<<ans<<"\n";
        
    }
    return 0;
}