Binary Indexed Trees(树状数组)
1.lowbit
lowbit(x)是x的二进制表达式中最低位的1所对应的值。比如,6的二进制是110,所以lowbit(6)=2。
lowbit(x) = x&(-x)
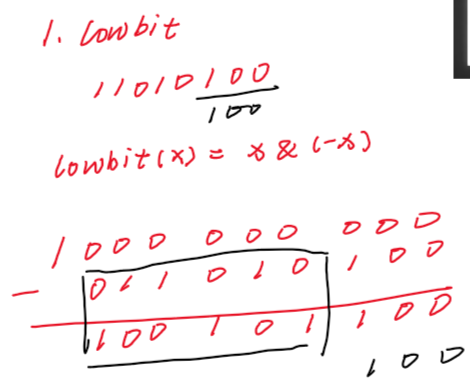
2.定义,查询,修改,前缀最值(eg1)
\(a1,a2,...,an\)
能在log的时间复杂度下完成:
-
单点加,\(ai+=d\)
-
查询前缀和\(\sum_{i = 1}^{x}ai\)
树状数组定义:
\(c_i = a_{i-lowbit(i)+1到i}\)的和
画个图...
对于树状数组,字面意思就是树状的数组

变形一下:

现定义每一列顶端节点为c数组,如图:
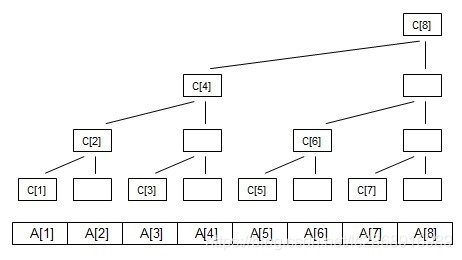
c[i]表示子树的叶子节点的权值和
c[1] = a[1]
c[2] = a[1]+a[2]
c[3] = a[3]
c[4] = a[1]+a[2]+a[3]+a[4]
c[5] = a[5]
c[6] = a[5]+a[6]
c[7] = a[7]
c[8] = a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]
修改和查询:
先看查询操作:
举个栗子:
i = 7,sum[7] = a[1]+a[2]+...+a[7]
而c[4] = a[1]+a[2]+a[3]+a[4],c[6] = a[5]+a[6],c[7] = a[7]
那么,sum[7] = c[4]+c[6]+c[7]
改写为二进制有:sum[(111)] = c[(100)]+c[(110)]+c[(111)]
ans += c[7]
lowbit(7) = (001) ,7-lowbit(7) = 6(110),ans+= c[6]
lowbit(6) = (010),6-lowbit(6) = 4(100),ans+=c[4]
lowbit(4) = (100),4-lowbit(4) = 0(000) break;
画个图理解一下:
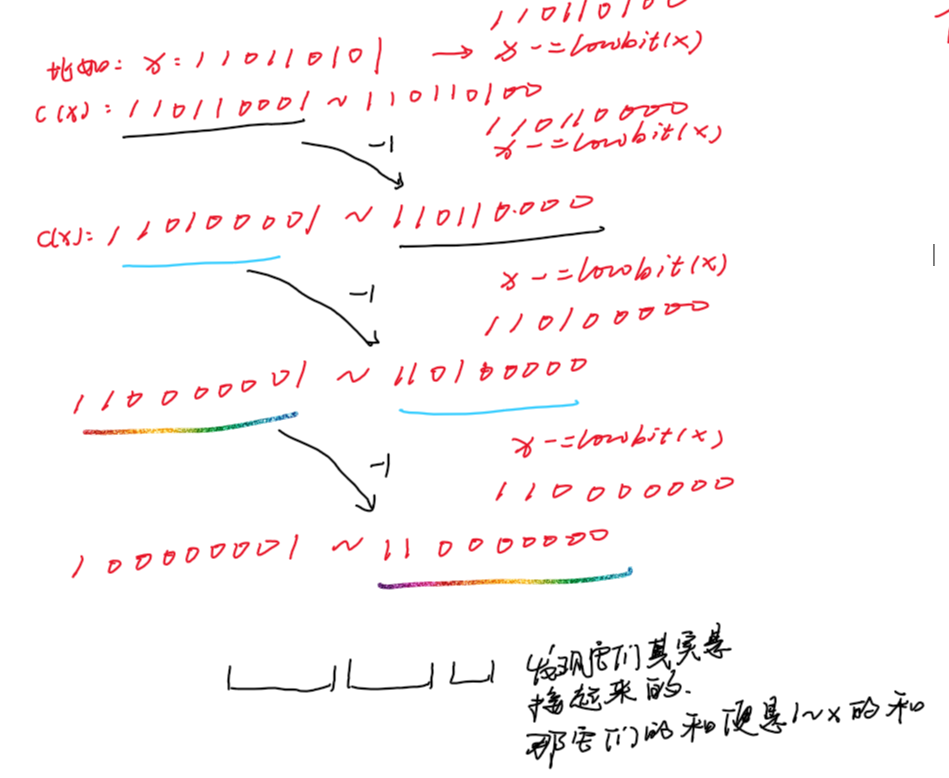
对于单点更新:向上更新区间长度为lowbit(i)所代表的节点的值

比如我要更新a[1]的值,那么我需要向上更新c[1],c[2],c[4],c[8]的值
写成二进制:
c[(001)],c[(010)],c[(100)],c[(1000)]
lowbit(1) = (001) 1+lowbit(1) = 2(010) ,c[2]+=val
lowbit(2) = (010) 2+lowbit(2) = 4(100) ,c[4]+=val
lowbit(4) = (100) 4+lowbit(4) = 8(1000) ,c[8]+=val
c[1],c[2],c[4],c[8]都包含a[1],所以实际上更新a[1]就是更新包含a[1]的节点的信息。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 201000;
int a[N],n;
ll c[N];
ll query(int x){//1...x
ll s = 0;
for(;x;x-=x&(-x))
s += c[x];
return s;
}
void modify(int x,ll s){//a[x]+=s
for(;x<=n;x+=x&(-x))
c[x]+=s;
}
例题1.树状数组1
给n个数a1,a2,a3,…,an。
支持q个操作:
1 x d,修改\(ax=d\)。2 x,查询\(\sum_{i=1}^{x}ai\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 201000;
int n,q;
int a[N];
ll c[N];
ll query(int x){//1...x
ll s = 0;
for(;x;x-=x&(-x))
s += c[x];
return s;
}
void modify(int x,ll s){//a[x]+=s
for(;x<=n;x+=x&(-x))
c[x]+=s;
}
int main()
{
cin>>n>>q;
for(int i = 1;i<=n;i++)
{
cin>>a[i];
modify(i,a[i]);
}
for(int i = 1;i<=q;i++)
{
int op;
cin>>op;
if(op==1)
{
int x,d;
cin>>x>>d;
modify(x,d-a[x]);
a[x] = d;
}
else
{
int x;
cin>>x;
cout<<query(x)<<endl;
}
}
return 0;
}
区间最值
树状数组最基本的功能是加速前缀和的更新。
查询前缀和操作用数组实现是O(1)的,但是树状数组是O(logn)的,
但是相较于数组,树状数组优点是单点更新的时间复杂度是O(logn),而数组是O(n)的,这使得在大规模更新时,树状数组更优。
总而言之,遇到不断更新前缀的操作的时候可以考虑树状数组。
1. 单点更新
对于最值的单点更新和前缀和的单点更新不同,前缀和的单点更新只需考虑当前点修改以后会对后面的数产生什么影响。前缀和只需要给定一个增量,然后对x以及后面所有的x+lowbit(x)进行修改即可。
而对于最值,b[x]数组表示的是[x-lowbit(x)+1,x]这个区间的最值,我们不知道x以及后面所有的x+lowbit(x)处改变的增量是多少,只能对这个区间所有值再求一次最值。这样看是不是复杂度已经到O(nlongn)了。
但是我们发现,对[x-lowbit(x)+1,x]有影响的并不是整个区间,而是\(x,x-2^0,x-2^1,...,x-2^k\)其中(\(2^k<lowbit(x)\))
举个栗子:
对于\(x=10010000\)
\(=10001000 + lowbit(10001000) = 10001000+1000 = 10001000 + 2^3\)
\(=10001100 + lowbit(10001100) = 10001000+100 = 10001100 + 2^2\)
\(=10001110 + lowbit(10001110) = 10001000+10 = 10001110 + 2^1\)
\(=10001111 + lowbit(10001111) = 10001000+1 = 10001111 + 2^0\)
因此,更新x处的b[x]的值,复杂度仅为logn级别的,再加上x后续的所有的x+lowbit(x),总的复杂度就是O(logn*logn)级别的了
#include<bits/stdc++.h>
using namespace std;
void update(int x)
{
for(;x<=N;x+=x&(-x))
{
b[x] = a[x];
int lx = x&(-x);//[x-lowbit(x)+1,x]的区间长度
for(int i = 1;i<lx;i<<=1)
b[x] = max(b[x],b[x-i]);
}
}
2.区间查询
对于前缀和的区间查询可以用sum[r]-sum[l-1],但是区间最值显然是不可以的。
首先我们明确:我们要求区间[x,y]上的最值,是与[1,x-1]是没有任何关系的
以求最大值为例:
当y-lowbit(y)>=x时,[x,y]区间包含了[y-lowbit(y)+1,y]区间,是可以直接使用b[y]的值。
\(query(x,y) = max(b[y],query(x,y-lowbit(y)))\)
但是当y-lowbit(y)<x时候,上述关系不成立,先用a[y]值,再将y-1
\(query(x,y) = max(a[y],query(x,y-1)\)
时间复杂度也同样是O(logn*logn)的
例题
P1531 I Hate It - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10;
int a[N],b[N];
inline int lowbit(const int &x) { return x&-x; }
void update(int x)
{
for(;x<=N;x+=lowbit(x))
{
b[x] = a[x];
int lx = lowbit(x);//[x-lowbit(x)+1,x]的区间长度
for(int i = 1;i<lx;i<<=1)
b[x] = max(b[x],b[x-i]);
}
}
int query(int x,int y)
{
int ans = 0;
for(;y>=x;)
{
ans = max(ans,a[y]),--y;
while(y-lowbit(y)>=x)
{
ans = max(ans,b[y]);
y-=lowbit(y);
}
}
return ans;
}
int n,m;
int main()
{
cin>>n>>m;
for(int i = 1;i<=n;i++)
cin>>a[i],update(i);
for(int i = 1;i<=m;i++)
{
char op;
int x,y;
cin>>op>>x>>y;
if(op=='Q')
cout<<query(x,y)<<"\n";
else
{
if(a[x]<y)
{
a[x] = y;
update(x);
}
}
}
return 0;
}
3.应用(eg2,3)
eg2.逆序对2
请问数组 \(a\) 的逆序对一共有多少个?形式化的说,请求出有多少组$ (i,j)\(满足\) i<j$ 并且 \(ai>aj\)。
思路:
-
扫描线思想,静态=>动态
for(j = 1~n)
统计\(a_1\)~\(a_{j-1}\)里面有多少个>\(a_j\)的
我们有一个数据结构D,D里面存了\(a_1\)~\(a_{j-1}\)。
问题变成了我们要统计D里面有多少个\(>=a_j\)的,统计完之后,我们把\(a_j\)加入D中。我们再动态的过程中不断把答案加起来,就是所有的逆序对数了。
我们把一个静态的问题转化为一个动态带修改的问题。
-
对权值开树状数组
对D里面,我们要做的是a.加入一个数 b.查询有多少个\(>=a_j\)的数
比如我们加入一个数\(a_i\),那我们再\(D[a[i]]\)位置++
要查询多少个\(>=a_j\)的数,即查询\(a_j\)后面又多少个1,实际上是做一个后缀查询。\(for(i = a_{j+1}\)~\(n)ans += D[i]\)
总结:
①D[a[j]]+=1
②后缀查询
这里跟树状数组没什么区别了,唯一区别就是前缀查询变成了后缀,我们把所有东西翻过来,就变成前缀和
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 201000;
int n;
int a[N];
ll c[N];
ll query(int x){//1...x
ll s = 0;
for(;x;x-=x&(-x))
s += c[x];
return s;
}
void modify(int x,ll s){//a[x]+=s
for(;x<=n;x+=x&(-x))
c[x]+=s;
}
int main()
{
cin>>n;
for(int i = 1;i<=n;i++)
{
cin>>a[i];
a[i] = n+1-a[i];
}
ll ans = 0;
for(int i = 1;i<=n;i++)
ans += query(a[i]),modify(a[i],1);
cout<<ans<<endl;
return 0;
}
eg3.树状数组2
有\(n\)个数\(a1,a2,a3,…,an\)一开始都是0。
支持\(q\)个操作:
1 l r d,令所有的\(a_i(l≤i≤r)\)加上\(d\)。2 x,查询\((\sum_{i=1}^{x}ai) \bmod 2^{64}\)。
操作:区间加+单点查询
差分:\(d_i = a_i - a_{i-1}\)
前缀和:\(a_i = d_1+d_2...+d_i\)
\([l,r]+1\)
\(d_l+=1,d_{r+1}-=1\)
查询单点其实就是个d的前缀和\(\sum_{i = 1}^{x}a_i\)
\(a_1 = d_1\)
\(a_2 = d_1+d_2\)
\(a_3 = d_1+d_2+d_3\)
那么\(a_1+a_2+a+3 = 3d_1+2d_2+d_3\)
那么$a_x = xd_1+(x-1)d_2+...+d_x = \sum_{i = 1}^{x}(x+1-i)*d_i $
化简一下$(x+1)(\sum_{i = 1}^{x}d_i)-(\sum_{i = 1}^{x}i*d_i) $
那么我们只需要维护出\(d_i\)的前缀和和\(i*d_i\)的前缀和就行了。这两个东西我们开两个树状数组取维护它。
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long u64;
const int N = 201000;
int n,q;
int a[N];
template<class T>
struct BIT
{
T c[N];
int size;
void resize(int s){size = s;}
T query(int x){//1...x
assert(x<=size);
T s = 0;
for(;x;x-=x&(-x))
s += c[x];
return s;
}
void modify(int x,T s){//a[x]+=s
assert(x!=0);//注意:树状数组下标不能是0,因为lowbit会死循环
for(;x<=n;x+=x&(-x))
c[x]+=s;
}
};
BIT<u64>c1,c2;//c1:d[i],c2:i*d[i]
int main()
{
cin>>n>>q;
c1.resize(n),c2.resize(n);
for(int i = 1;i<=q;i++)
{
int op;
cin>>op;
if(op==1)
{
int l,r;
u64 d;
cin>>l>>r>>d;
c1.modify(l,d);
c1.modify(r+1,-d);
c2.modify(l,l*d);
c2.modify(r+1,(r+1)*(-d));
}
else
{
int x;
cin>>x;
u64 ans = (x+1)*c1.query(x)-c2.query(x);
cout<<ans<<endl;
}
}
return 0;
}
4.二分(eg4)
树状数组上二分,其实更像是倍增。
树状数组的神奇之处在于它本身的结构就是基于二进制实现
方法:从大到小枚举幂次,如果能移动,就移动
例题:
给\(n\)个数\(a1,a2,a3,…,an。\)
支持q个操作:
1 x d,修改\(a_x=d\)。2 s,查询最大的\(T(0≤T≤n)\)满足\(\sum_{i=1}^{T}ai≤s\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 201000;
int n,q;
int a[N];
ll c[N];
/*
写法1:
ll query(ll s){
ll t = 0;
int pos = 0;
// for(j = log(n)~0)
// pos 是当前的位置
// t 记录的是1~pos的和
// pos' = pos+2^j
for(int j = 18;j>=0;j--)
{
if(pos+(1<<j)<=n&&t+c[pos+(1<<j)]<=s)
{
pos += (1<<j);
t+=c[pos];
}
}
return pos;
}
*/
//写法2:
ll query(ll s){
int pos = 0;
for(int j = 18;j>=0;j--)
{
if(pos+(1<<j)<=n&&c[pos+(1<<j)]<=s)
{
pos += (1<<j);
s-=c[pos];
}
}
return pos;
}
void modify(int x,ll s){//a[x]+=s
for(;x<=n;x+=x&(-x))
c[x]+=s;
}
int main()
{
cin>>n>>q;
for(int i = 1;i<=n;i++)
{
cin>>a[i];
modify(i,a[i]);
}
for(int i = 1;i<=q;i++)
{
int op;
cin>>op;
if(op==1)
{
int x,d;
cin>>x>>d;
modify(x,d-a[x]);
a[x] = d;
}
else
{
ll s;
cin>>s;
cout<<query(s)<<endl;
}
}
return 0;
}
5.高维树状数组(eg5)
\(c[i][j]\)
\(a[i-lowbit[i]+1\)~\(i]\) \([j-lowbit[j]+1\)~\(j]\)
eg5.二维树状数组
给\(n×m\)个数\(a_{1,1},a_{1,2},a_{1,3},…,a_{1,m},…,a_{n,m}\)。
支持\(q\)个操作:
1 x y d,修改\(a_{x,y}=d\)。
2 x y,查询\(\sum_{i = 1}^{x}a_{i,j}\)。
时间复杂度\(O(log^2(n))\)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 510;
int n,m,q;
int a[N][N];
ll c[N][N];
ll query(int x,int y){
ll s = 0;
for(int p = x;p;p-=p&(-p))
for(int q = y;q;q-=q&(-q))
s += c[p][q];
return s;
}
void modify(int x,int y,ll s){
for(int p = x;p<=n;p+=p&(-p))
for(int q = y;q<=m;q+=q&(-q))
c[p][q]+=s;
}
int main()
{
cin>>n>>m>>q;
for(int i = 1;i<=n;i++)
{
for(int j = 1;j<=m;j++)
{
cin>>a[i][j];
modify(i,j,a[i][j]);
}
}
for(int i = 1;i<=q;i++)
{
int op;
cin>>op;
if(op==1)
{
int x,y,d;
cin>>x>>y>>d;
modify(x,y,d-a[x][y]);
a[x][y] = d;
}
else
{
int x,y;
cin>>x>>y;
cout<<query(x,y)<<endl;
}
}
return 0;
}
6.数据结构优化DP
例题1:最大和上升子序列2
\(f[i]\)表示以\(i\)结尾和最大的上升子序列
\(f[i] = max_{1\le j<i,a_j<a_i}(f[j])+a[i]\)
直接做的时间复杂度是\(O(N^2)\)
考虑优化一下。
\(max_{1\le j <i,a_j<a{i}}(f[j])\)对这部分优化
定义一个\(p\)数组,\(p_x\)表示\(a_j = x\)最大的\(dp_j\),相当于我们对值域开一个数组
\(f[i] = max_{1\le k < a_i}p_k+a_i\) 前缀最大值查询
\(p[a[i]] = max(p[a[i]],f[i])\) 单点修改
我们想到了一个数据结构:树状数组。
但对于树状数组我们的限制很多,比如:1.我们的查询只能做前缀的,不像前缀和那样减一下求,树状数组是不行的。2.对于前缀最大值查询,我们的修改操作只能往大了改,往小了改不行。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5+10,M = 2e5;
int a[N];
ll c[N],dp[N];
ll query(int x)
{
ll s = 0;
for(;x;x-= x&(-x))
s = max(s,c[x]);
return s;
}
void modify(int x,ll s)
{
for(;x<=M;x+=x&(-x))
{
c[x] = max(c[x],s);
}
}
int main()
{
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int n;
cin>>n;
for(int i = 1;i<=n;i++)
cin>>a[i];
ll ans = 0;
for(int i = 1;i<=n;i++)
{
dp[i] = query(a[i]-1)+a[i];
modify(a[i],dp[i]);
ans = max(ans,dp[i]);
}
cout<<ans<<endl;
return 0;
}
例题2:Partition Game(线段树)
\(hater\)扔给你一个长度为\(n\)序列,定义其中一个连续子序列\(t\)的代价为:
其中\(set(t)\)表示该子序列的元素集合,\(last(x)\)表示\(x\)在该子序列中最后一次出现的位置,\(first(x)\)表示\(x\)在该子序列中第一次出现的位置。
也就是说一个连续子序列的贡献为对于其中每种元素最后一次出现的位置与第一次出现的位置的下标差的和。
现在你要把原序列划分成\(k\)个连续子序列,求最小代价和。
其中\(1\leq n\leq35000,1\leq k\leq min(n,100),1\leq a_i \leq n\)。
思路:
最暴力的写法:\(dp[i][j]\)表示前\(i\)个元素切成\(j\)段的最小代价
\(dp[i][j] = min(dp[k][j-1])+w[k+1][i]\) 其中:\(w[k+1][i]\)就是\(k+1\)到\(i\)为一段的代价
考虑用数据结构优化:\(min(dp[k][j-1])\)
①:考虑用\(j\)分层
\(j-1 ->j\)
\(f[i] = dp[i][j-1]\)
\(g[i] = dp[i][j]\)
\(g[i] = min(f[k]+w[k+1][i])\)
②:令\(h[k] = f[k]+w[k+1][i]\)
\(i->i+1\):如果\(a_{i+1}\)没在\([k+1,i]\)中出现过,它的贡献就\(0\),否则加上\(i+1\)减去上一次出现的位置。
那么我们需要实现:前缀加,前缀最小值
时间复杂度\(NKlog\)





