scanning line(扫描线)
1.1扫描线的思想以及在几何问题上的应用(eg1,3)
二维数点
平面上有n个点(xi,yi)。
回答q个询问,每个询问给定一个矩形[X1,X2]×[Y1,Y2],询问矩形里面有多少个点。
因为有1e9的范围,我们离散化一下,我们只关心顺序,不关心具体是多少
这里相当于只需要把原来的点的坐标离散化,查询的时候直接二分找到小于等于他的第一个坐标即可。
思想:
①扫描线+容斥
②离线
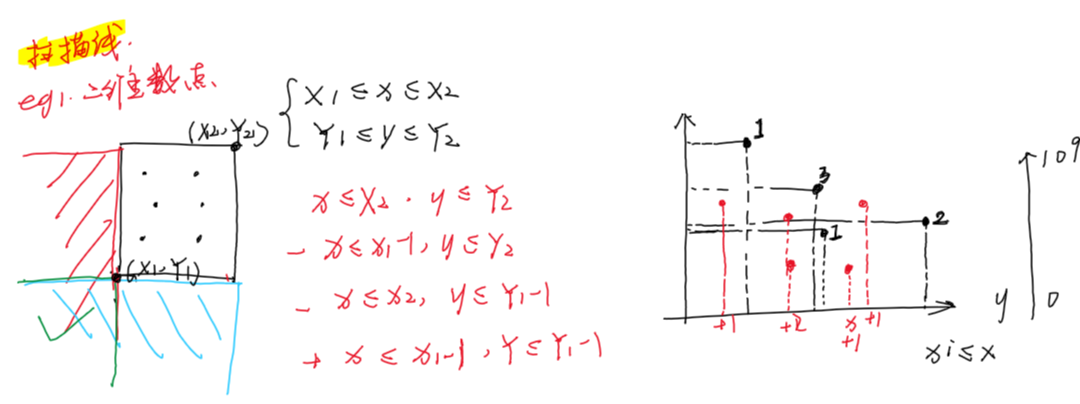
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N = 201000; vector<int>vx; vector<array<int,4>>event;; int n,q,m; int a[N],ans[N]; int c[N]; int query(int x){//1...x ll s = 0; for(;x;x-=x&(-x)) s += c[x]; return s; } void modify(int x,int s){//a[x]+=s for(;x<=m;x+=x&(-x)) c[x]+=s; } int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n>>q; for(int i = 1;i<=n;i++) { int x,y; cin>>x>>y; vx.push_back(x); //y坐标,类型,x坐标 event.push_back({y,0,x}); } for(int i = 1;i<=q;i++) { int x1,x2,y1,y2; cin>>x1>>x2>>y1>>y2; //用容斥 //y坐标,类型1-,2+,x坐标,哪一个询问 //0,1,2的设置其实还包含了希望哪个事件先发生,坐标一样的话,我们希望先插入再查询 event.push_back({y2,2,x2,i}); event.push_back({y1-1,2,x1-1,i}); event.push_back({y2,1,x1-1,i}); event.push_back({y1-1,1,x2,i}); } sort(event.begin(), event.end()); sort(vx.begin(), vx.end()); //去重 vx.erase(unique(vx.begin(), vx.end()),vx.end()); m = vx.size(); for(auto evt:event) { if(evt[1]==0){//插入 int y = lower_bound(vx.begin(), vx.end(),evt[2])-vx.begin()+1;//树状数组是1base的 modify(y,1); } else{//查询<=它的最后一个位置,即第一个>它的位置-1 int y = upper_bound(vx.begin(), vx.end(),evt[2])-vx.begin()-1+1;//树状数组是1base的 int tmp = query(y); if(evt[1]==1)ans[evt[3]] -= tmp; else ans[evt[3]] += tmp; } } for(int i = 1;i<=q;i++) cout<<ans[i]<<'\n'; return 0; }
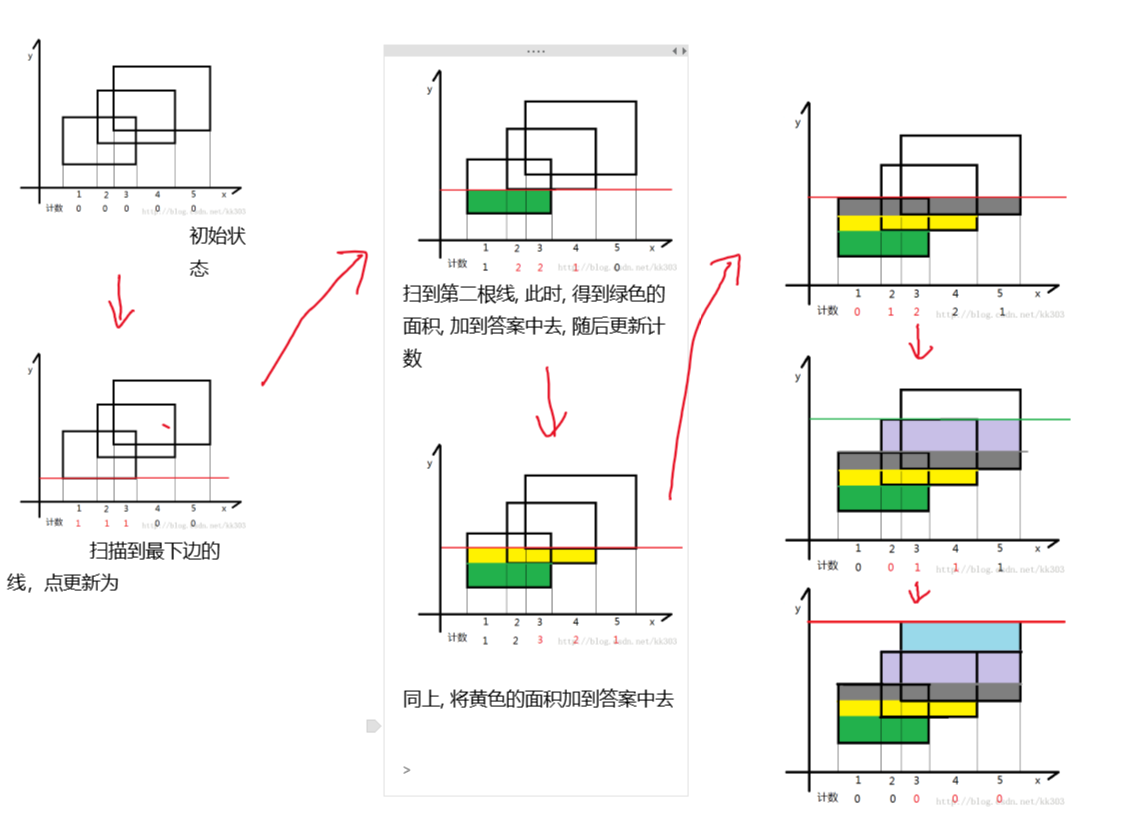
矩形面积并
思路:
x坐标离散化
cnt>0覆盖,cnt=0未被覆盖
用线段树记录cnt的最小值,也就是被覆盖次数的最小的段。
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N = 201000; vector<int>vx; vector<array<int,4>>event;; int n,q,m; struct info { int minv,mincnt; }; info operator+(const info &l,const info &r) { info a; a.minv = min(l.minv,r.minv); if(l.minv==r.minv)a.mincnt = l.mincnt + r.mincnt; else if(l.minv<r.minv)a.mincnt = l.mincnt; else a.mincnt = r.mincnt; return a; } struct node{ int t; info val; }seg[N*8]; void update(int id) { seg[id].val = seg[id*2].val+seg[id*2+1].val; } void settag(int id,int t) { seg[id].val.minv = seg[id].val.minv+t; seg[id].t = seg[id].t + t; } void pushdown(int id) { if(seg[id].t!=0) { settag(id*2,seg[id].t); settag(id*2+1,seg[id].t); seg[id].t = 0; } } void build(int id,int l,int r) { if(l==r) seg[id].val = {0,vx[r]-vx[r-1]}; else { int mid = (l+r)>>1; build(id*2,l,mid); build(id*2+1,mid+1,r); update(id); } } void modify(int id,int l,int r,int x,int y,ll t){ if(l==x&&r==y) { settag(id,t); return; } int mid = (l+r)/2; pushdown(id); if(y<=mid) modify(id*2,l,mid,x,y,t); else if(x>mid) modify(id*2+1,mid+1,r,x,y,t); else{ modify(id*2,l,mid,x,mid,t),modify(id*2+1,mid+1,r,mid+1,y,t); } update(id); } int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n; for(int i = 1;i<=n;i++) { int x1,x2,y1,y2; cin>>x1>>x2>>y1>>y2; vx.push_back(x1); vx.push_back(x2); //y坐标,类型0,x坐标 event.push_back({y1,1,x1,x2}); event.push_back({y2,-1,x1,x2}); } sort(event.begin(), event.end()); sort(vx.begin(), vx.end()); //去重 vx.erase(unique(vx.begin(), vx.end()),vx.end()); m = vx.size()-1;//段数=点数-1 build(1,1,m); int prey = 0; int totlen = seg[1].val.mincnt; ll ans = 0; for(auto evt:event) { int cov = totlen; if(seg[1].val.minv==0) cov = totlen - seg[1].val.mincnt; ans += (ll)(evt[0]-prey)*cov; prey = evt[0]; int x1 = lower_bound(vx.begin(), vx.end(),evt[2])-vx.begin()+1; int x2 = lower_bound(vx.begin(), vx.end(),evt[3])-vx.begin(); if(x1>x2)continue; modify(1,1,m,x1,x2,evt[1]); } cout<<ans<<endl; return 0; }
补充:矩形周长并
思路:和上一题矩形面积并思路差不多,也是用扫描线扫,不过没有面积那么好处理。对于面积,只用有覆盖的地方*高度的加和就是答案了,但是周长的话上边界不能想面积那样不管,周长的话要考虑上边界在哪是要的。
那么做法是:
对于矩形嘛,我们考虑扫两边,竖着扫再横着扫。这里以竖着扫为例。
我们竖着扫,也就是for一遍y,那么只需要对x进行离散化即可。
再建树,用来记录最小值和最小值出现的次数。
注意:我们离散化记录的是点,而线段树我们记录的线段。
也就是说记录的是[L+1,R]这一个线段,那么用lower_bound求到x1要+1。
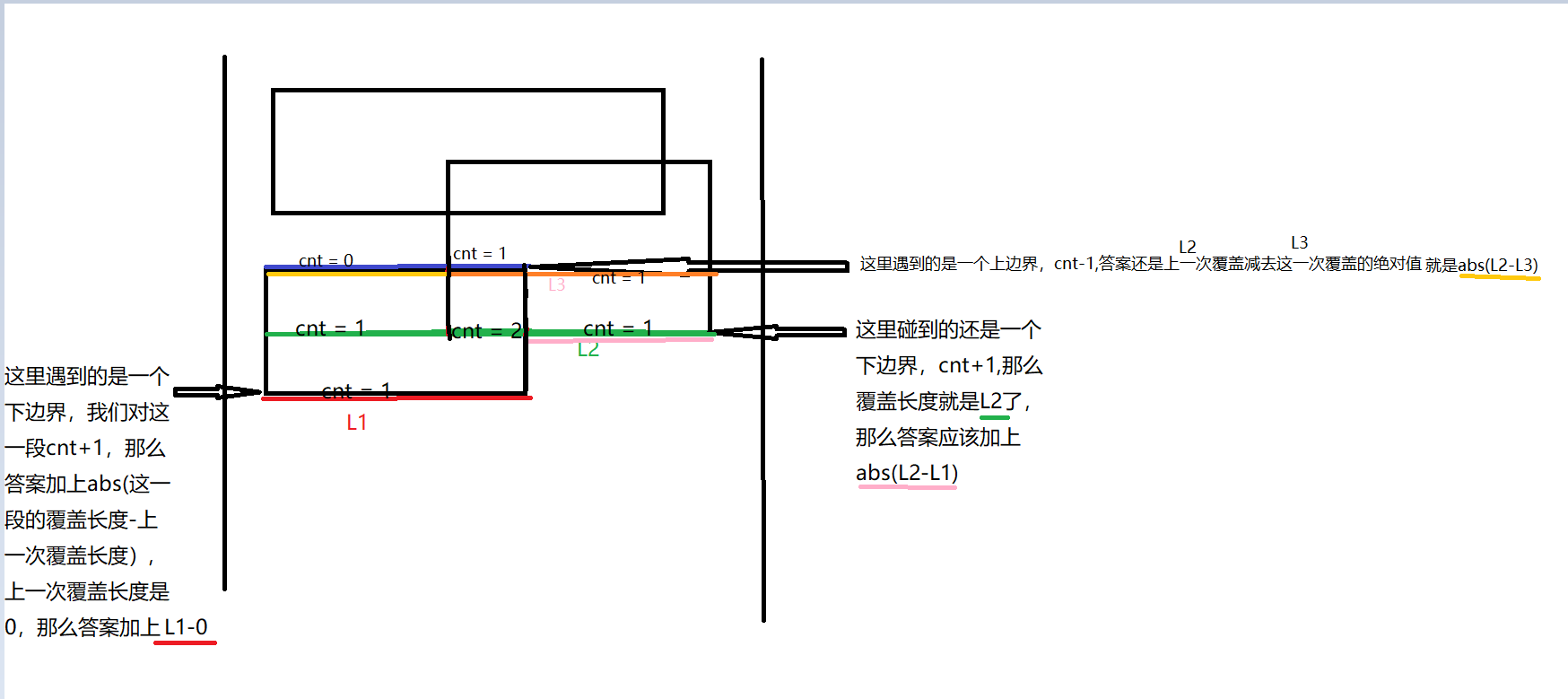
然后开始扫描,遇到的如果是下边界,对于x1到x2这一段要cnt+1。遇到的如果是下边界的话cnt-1。那么如何统计答案呢?
我们遇到一条与扫描线平行的线段时,答案加上【(上一条覆盖的长度-这一次覆盖的长度)的绝对值】即:ans += abs(precnt-nowcnt)
这句话怎么理解呢?
我们画图理解一下...
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N = 201000; vector<int>vx,vy; vector<array<int,4>>event1,event2; int n; struct info { int minv,mincnt; }; info operator+(const info &l,const info &r) { info a; a.minv = min(l.minv,r.minv); if(l.minv==r.minv)a.mincnt = l.mincnt + r.mincnt; else if(l.minv<r.minv)a.mincnt = l.mincnt; else a.mincnt = r.mincnt; return a; } struct node{ int t; info val; }seg[N*8]; void update(int id) { seg[id].val = seg[id*2].val+seg[id*2+1].val; } void settag(int id,int t) { seg[id].val.minv = seg[id].val.minv+t; seg[id].t = seg[id].t + t; } void pushdown(int id) { if(seg[id].t!=0) { settag(id*2,seg[id].t); settag(id*2+1,seg[id].t); seg[id].t = 0; } } void build(int id,int l,int r) { if(l==r) seg[id].val = {0,vx[r]-vx[r-1]};//mincnt就是区间长度,比如对于第一段就是第1个端点-第0个端点 else { int mid = (l+r)>>1; build(id*2,l,mid); build(id*2+1,mid+1,r); update(id); } } void build2(int id,int l,int r) { if(l==r) seg[id].val = {0,vy[r]-vy[r-1]};//mincnt就是区间长度,比如对于第一段就是第1个端点-第0个端点 else { int mid = (l+r)>>1; build2(id*2,l,mid); build2(id*2+1,mid+1,r); update(id); } } void modify(int id,int l,int r,int x,int y,ll t){ if(l==x&&r==y) { settag(id,t); return; } int mid = (l+r)/2; pushdown(id); if(y<=mid) modify(id*2,l,mid,x,y,t); else if(x>mid) modify(id*2+1,mid+1,r,x,y,t); else{ modify(id*2,l,mid,x,mid,t),modify(id*2+1,mid+1,r,mid+1,y,t); } update(id); } int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n; for(int i = 1;i<=n;i++) { int x1,y1,x2,y2; cin>>x1>>y1>>x2>>y2; vx.push_back(x1),vx.push_back(x2); event1.push_back({y1,-1,x1,x2}); event1.push_back({y2,1,x1,x2}); vy.push_back(y1),vy.push_back(y2); event2.push_back({x1,-1,y1,y2}); event2.push_back({x2,1,y1,y2}); } sort(event1.begin(),event1.end()); sort(vx.begin(),vx.end()); vx.erase(unique(vx.begin(),vx.end()),vx.end()); sort(event2.begin(),event2.end()); sort(vy.begin(),vy.end()); vy.erase(unique(vy.begin(),vy.end()),vy.end()); int m = vx.size()-1; build(1,1,m); int precnt = 0,nowcnt = 0; int totlen = seg[1].val.mincnt; ll ans = 0; for(auto evt:event1) { int x1 = lower_bound(vx.begin(),vx.end(),evt[2])-vx.begin()+1; int x2 = lower_bound(vx.begin(),vx.end(),evt[3])-vx.begin(); if(x1>x2)continue; modify(1,1,m,x1,x2,-evt[1]); nowcnt = totlen; if(seg[1].val.minv==0) nowcnt -= seg[1].val.mincnt; //cout<<"now = "<<nowcnt<<" pre = "<<precnt<<endl; ans += abs(nowcnt-precnt); precnt = nowcnt; } //cout<<ans<<endl; m = vy.size()-1; memset(seg,0,sizeof(seg)); build2(1,1,m); precnt = 0; totlen = seg[1].val.mincnt; for(auto evt:event2) { int y1 = lower_bound(vy.begin(),vy.end(),evt[2])-vy.begin()+1; int y2 = lower_bound(vy.begin(),vy.end(),evt[3])-vy.begin(); if(y1>y2)continue; modify(1,1,m,y1,y2,-evt[1]); nowcnt = totlen; if(seg[1].val.minv==0) nowcnt -= seg[1].val.mincnt; ans += abs(nowcnt-precnt); precnt = nowcnt; } cout<<ans<<endl; return 0; } /* heck 数据 2 0 0 4 4 0 4 4 8 注意顺序,如果有重边应该先加再减! */
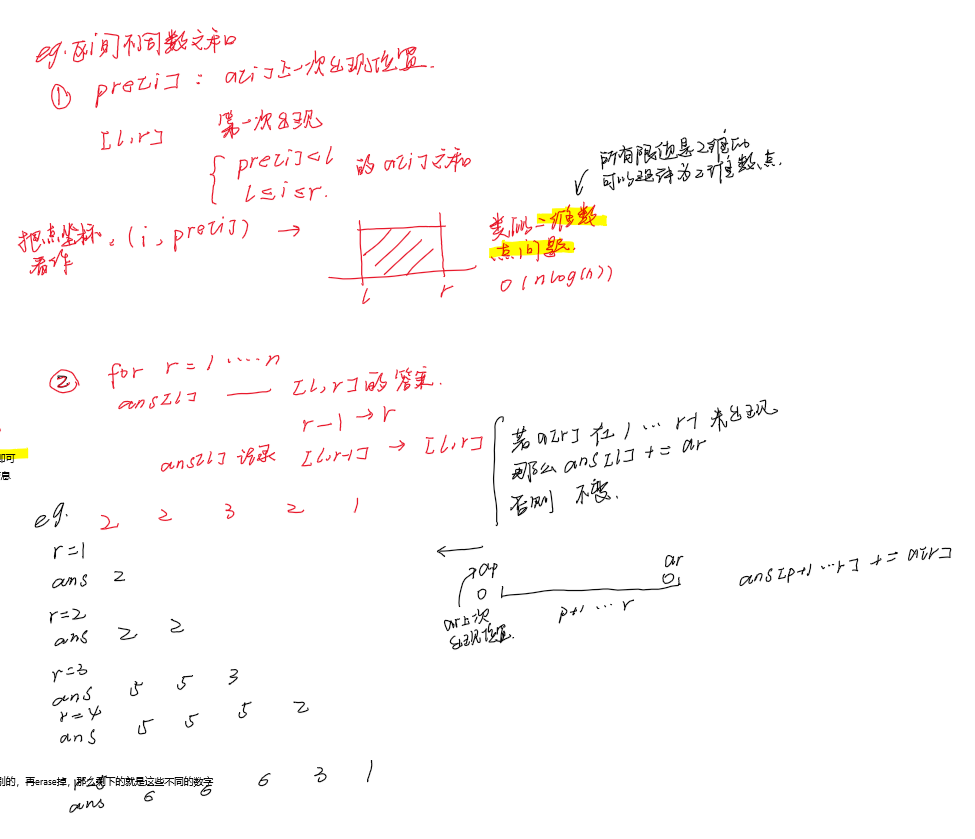
1.2 扫描线在序列问题上的应用(eg2)
区间不同数之和
有\(n\)个数\(a1,a2,…,an\)。
有\(q\)组询问,每次给一个区间\([l,r]\),求区间里不同的数字之和,也就是说同一个数字出现多次只算一次。
思路:
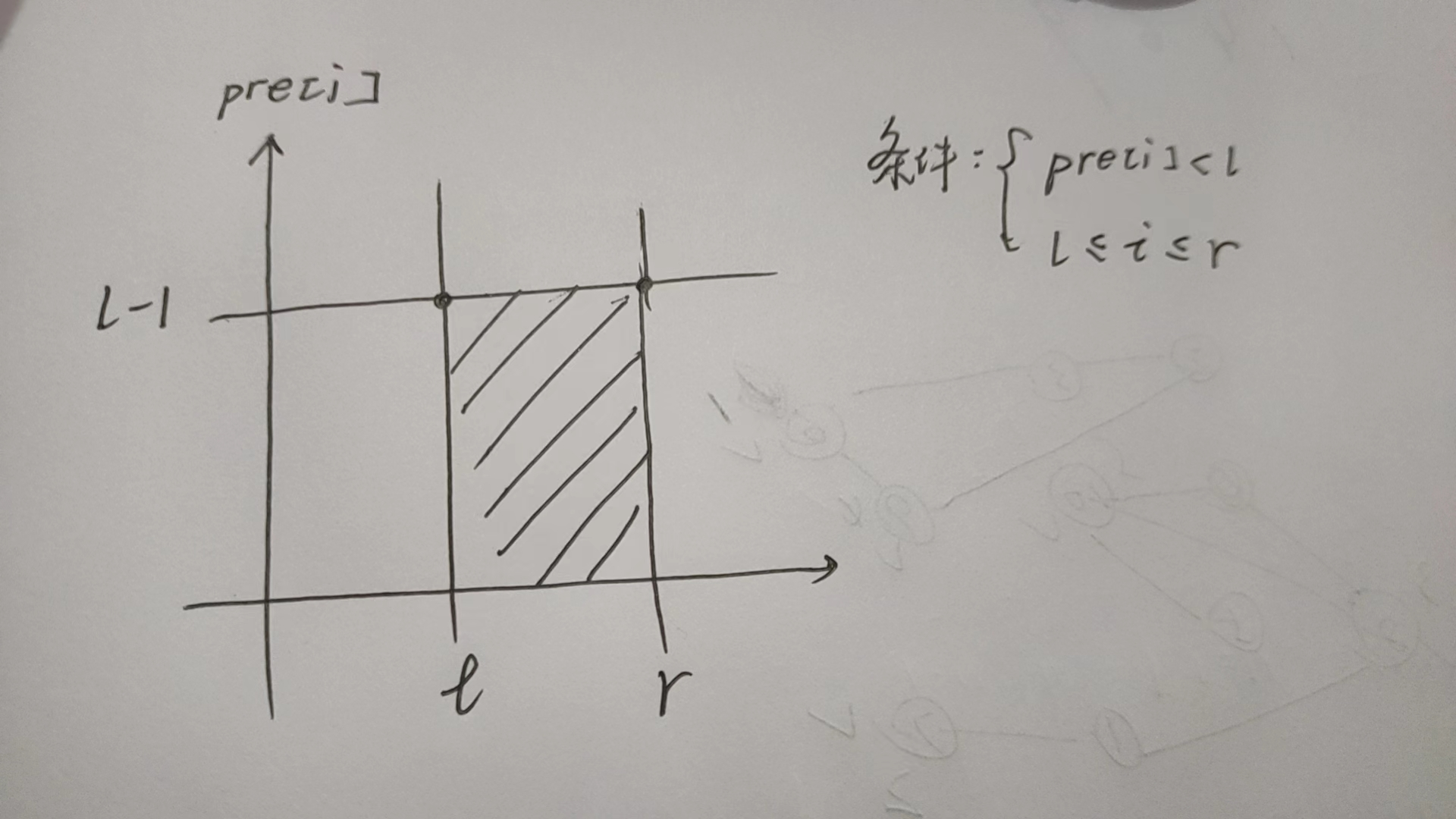
①思路一:\(pri[i]\)表示\(a[i]\)上一次出现的位置(只统计第一次出现)
\(pri[i]<l\)和\(l<=i<=r\)满足这两个条件的\(ai\)之和。
转化为二维数点问题,所有限制是两维的都可以看成二维数点。
把一个点坐标看成\((i,pri[i])\),$$\begin{cases} pri[i]<l\\ l<=i<=r \end{cases} \tag{1} $$满足这两个条件的\(ai\)之和。
因为我们对pre[]进行扫描,按pre[]的大小排序,for这pre[]这一维度进行扫描。
事件:
0. 插入:modify(i,a[i])
- 查询:query(r)-query(l-1)
#include<bits/stdc++.h> using namespace std; typedef long long ll; #define int long long const int N = 201000; vector<int>vx; vector<array<int,4>>event;; int n,q,m; int a[N],ans[N]; int c[N]; int pre[N],last[N]; int query(int x){//1...x ll s = 0; for(;x;x-=x&(-x)) s += c[x]; return s; } void modify(int x,int s){//a[x]+=s for(;x<=m;x+=x&(-x)) c[x]+=s; } signed main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n>>q; m = n; for(int i = 1;i<=n;i++) { cin>>a[i]; pre[i] = last[a[i]];//记录一个数上一次出现的位置 last[a[i]] = i; event.push_back({pre[i],0,i,a[i]}); } /* 对于一个区间[l,r] 满足条件的点需要: l<=i<=r pre[i]<l */ for(int i = 1;i<=q;i++) { int l,r; cin>>l>>r; event.push_back({l-1,1,l,i}); event.push_back({l-1,2,r,i}); } sort(event.begin(), event.end());//按pre[i]排序 for(auto evt:event) { if(evt[1]==0){//插入 modify(evt[2],evt[3]); } else{ if(evt[1]==1) ans[evt[3]] -= query(evt[2]-1); else ans[evt[3]] += query(evt[2]); } } for(int i = 1;i<=q;i++) cout<<ans[i]<<'\n'; 0; }
②思路二:for(r = 1~n)
维护\(ans[l] :[l,r]\)的答案
\(r-1——>r\) , \(ans[l]:[l,r-1]——>[l,r]\)
\(a_r\)在\([l,r-1]\)未出现,\(ans[l]+=a_r\),否则不变
比如对于\([l,r]\)一段,在\([l,p]\)上\(a_r\)出现过,在\([p+1,r]\)上没出现过,那么\(ans[p+1\)~\(r]+=a[r]\)
综上所述,我们要实现:
①区间加
②单点查询
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N = 201000; ll n,q,a[N],pos[N],ans[N]; vector<array<int,3>>qu[N]; ll c[N]; ll query(int x){//1...x ll s = 0; for(;x;x-=x&(-x)) s += c[x]; return s; } void modify(int x,ll s){//a[x]+=s for(;x<=n;x+=x&(-x)) c[x]+=s; } int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n>>q; for(int i = 1;i<=n;i++) cin>>a[i]; for(int i = 1;i<=q;i++) { int l,r; cin>>l>>r; qu[r].push_back({l,i}); } for(int r = 1;r<=n;r++) { int p = pos[a[r]]; modify(p+1,a[r]); modify(r+1,-a[r]); pos[a[r]] = r; for(auto que:qu[r]) { //ans[l]:[l,r]的答案 ans[que[1]] = query(que[0]); } } for(int i = 1;i<=q;i++) cout<<ans[i]<<'\n'; return 0; }
2.权值线段树之字典树(eg4)
异或第k小
给\(n\)个数字\(a1,a2,…,an\)。
你要回答\(m\)个询问,每次给定两个数\(x,k\)询问a1 xor x,a2 xor x,…,an xor x中从小到大排序中第\(k\)小的元素。
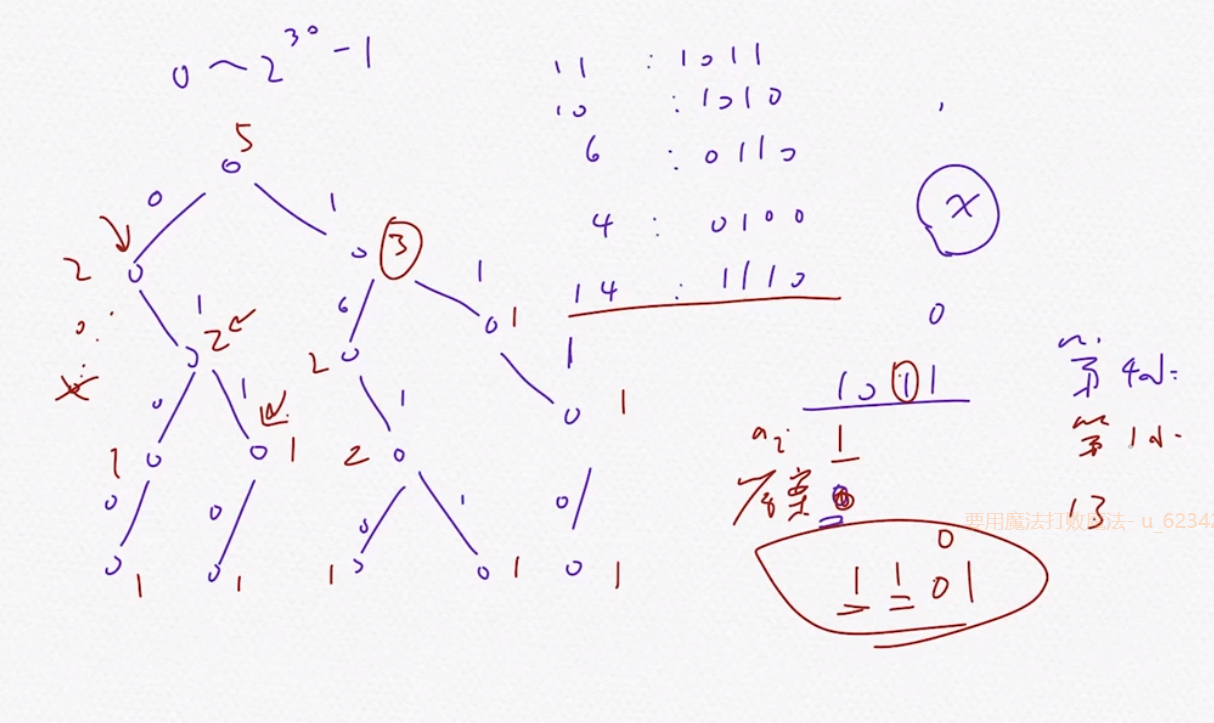
#include<bits/stdc++.h> using namespace std; const int N = 201000; const int M = 30;//0~2^30-1 int n,m,a[N]; struct node { int s[2]; int sz; }seg[N*32]; int tot = 0,root; int main() { cin>>n>>m; root = ++tot; for(int i = 0;i<n;i++) { int x; cin>>x; int p = root; for(int j = M-1;j>=0;j--) { seg[p].sz+=1; int w = (x>>j)&1; if(seg[p].s[w]==0)seg[p].s[w] = ++tot; p = seg[p].s[w]; } seg[p].sz+=1; } for(int i = 0;i<m;i++) { int x,k; cin>>x>>k; int ans = 0; int p = root; for(int j = M-1;j>=0;j--) { int w = (x>>j)&1; if(seg[seg[p].s[w]].sz>=k) { p = seg[p].s[w]; }else{ k -= seg[seg[p].s[w]].sz; ans^=1<<j; p = seg[p].s[w^1]; } } cout<<ans<<endl; } return 0; }
3.扫描线与权值线段树的总和运用(eg5)
mex
题意:
有一个长度为\(n\)的数组 \(a1,a2,…,an\)。
你要回答\(q\)个询问,每次给一个区间\([l,r]\),询问这个区间内最小没有出现过的自然数。
思路:
权值线段树+扫描线+线段树上二分
我们利用权值线段树,从\(1\)到\(n\)开始不断地加\(a[i]\)进去
权值线段树维护某个数最后一次出现在数组中的位置,初始所有数都没出现。
for(r = 1~n)
\(posx:\)x最后一次出现的位置,找到最小的x满足pos[x]<l
对于所有\(R = i\)的询问,我们利用\(L\)进行查询
去找到最后一次出现位置小于\(L\)的最小的数。
注意:这里权值是\(1e9\)但是\(n\)的范围是\(2e5\),那我们的\(mex\)肯定是小于\(n+1\)的,我们要对\(a[i]\)个\(n+1\)取\(min\).
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N = 201000; ll n,q,a[N],pos[N],ans[N]; vector<array<int,3>>qu[N]; struct node{ int val; }seg[N*4]; void update(int id) { seg[id].val = min(seg[id*2].val,seg[id*2+1].val); } void change(int id,int l,int r,int pos,int val){ if(l==r) { seg[id].val = val; return; } int mid = (l+r)/2; if(pos<=mid)change(id*2,l,mid,pos,val); else change(id*2+1,mid+1,r,pos,val); update(id); } int search(int id,int l,int r,int d) { if(l==r)return l; int mid = (l+r)>>1; if(seg[id*2].val<d)return search(id*2,l,mid,d); else return search(id*2+1,mid+1,r,d); } int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n>>q; for(int i = 1;i<=n;i++) cin>>a[i],a[i] = min(a[i],n+1); for(int i = 1;i<=q;i++) { int l,r; cin>>l>>r; qu[r].push_back({l,i}); } for(int r = 1;r<=n;r++) { //posx :x最后一次出现的位置, //最小的x满足pos[x]<l //pos[a[r]] = r; change(1,0,n+1,a[r],r); for(auto que:qu[r]) { ans[que[1]] = search(1,0,n+1,que[0]); } } for(int i = 1;i<=q;i++) cout<<ans[i]<<'\n'; return 0; }
4.从权值角度考虑
之前的题目大多数以下标的角度思考,本题考虑从权值角度考虑。
题意:
给你\(n\)个数\(a_1,a_2,…,a_n\)和\(q\)个询问:
l r x,询问\(a_l,a_{l+1},…,a_r\)中大于等于\(x\)的最小的数。
思路:
考虑用扫描线。先按权值为第一优先级排序,值一样的话先插入再查询。
因为先插入的是大的数,那再查小的数时,比它大的已经全部插入了,只需要查询区间最小值即可。那么我们需要用线段树实现区间最小值查询和单点修改。
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N = 201000; const int inf = 1<<30; int n,q; int a[N],ans[N]; struct node{ int minv; }seg[N*4]; void update(int id) { seg[id].minv = min(seg[id*2].minv,seg[id*2+1].minv); } void build(int id,int l,int r) { if(l==r) seg[id].minv = inf; else { int mid = (l+r)>>1; build(id*2,l,mid); build(id*2+1,mid+1,r); update(id); } } void change(int id,int l,int r,int pos,int val){ if(l==r) { seg[id].minv= val; } else { int mid = (l+r)/2; if(pos<=mid)change(id*2,l,mid,pos,val); else change(id*2+1,mid+1,r,pos,val); //重要!改完之后记得更新节点的信息 update(id); } } //O(logn) int query(int id,int l,int r,int x,int y) { if(l==x&&r==y)return seg[id].minv; int mid = (l+r)/2; if(y<=mid)return query(id*2,l,mid,x,y); else if(x>mid)return query(id*2+1,mid+1,r,x,y); else{ return min(query(id*2,l,mid,x,mid),query(id*2+1,mid+1,r,mid+1,y)); } } vector<array<int,4>> event; int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n>>q; for(int i = 1;i<=n;i++) { cin>>a[i]; event.push_back({-a[i],0,i});//我们希望从大到小for,那加个-号,,直接sort就是从大到小 // 设0,保证相同值情况下先插入 } for(int i = 1;i<=q;i++) { int l,r,x; cin>>l>>r>>x; event.push_back({-x,i,l,r}); } sort(event.begin(),event.end()); build(1,1,n); for(auto evt:event) { if(evt[1] == 0)change(1,1,n,evt[2],-evt[0]); else ans[evt[1]] = query(1,1,n,evt[2],evt[3]); } for(int i = 1;i<=q;i++) { if(ans[i]==inf)ans[i] = -1; cout<<ans[i]<<"\n"; } return 0; }




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
· AI与.NET技术实操系列(六):基于图像分类模型对图像进行分类