从Winograd算法看INT8量化及卷积加速原理

Winograd算法

主要参考了shine-lee大神的文章《卷积神经网络中的Winograd快速卷积算法》，详细请参阅原文。

Winograd算法论文出自CVPR 2016的一篇 paper：Fast Algorithms for Convolutional Neural Networks。

当前的流行的推理框架（加速器），如NCNN、NNPACK、TNN等，可以看到，对于卷积层，大家不约而同地采用了Winograd快速卷积算法，那到底Winograd算法是个什么呢。

问题定义

将一维卷积运算定义为$F(m,r)$

$\mu(F(m,r))=m+r-1$

在行列上分别进行一维卷积运算，可得到二维卷积，记为$F(m \times n,r \times s)$，输出为$m \times n$，卷积核为$r \times s$，则输入信号为$(m+r-1)(n+s-1)$，乘法数量至少为

$\mu(F(m \times n,r \times s))=\mu(F(m,r)) \mu(F(n,s))=(m+r-1)(n+s-1)$

若是直接按滑动窗口方式计算卷积，一维时需要$m \times r$次乘法，二维时需要$m \times n \times r \times s$次乘法，远大于上面计算的最少乘法次数。

使用Winograd算法计算卷积快在哪里？一言以蔽之：快在减少了乘法的数量，将乘法数量减少至$m+r-1$或$(m+r-1)(n+s-1)$。

怎么减少的？请看下面的例子。

一个例子 F(2, 3)

先以1维卷积为例，输入信号为$d=[d_{0} \quad d_{1} \quad d_{2} \quad d_{3}]^{T}$，卷积核为$g=[g_{0} \quad g_{1} \quad g_{2}]^{T}$，则卷积可写成如下矩阵乘法形式：

$F(2,3)= \begin{bmatrix} d_{0} & d_{1} & d_{2} \\ d_{1} & d_{2} & d_{3} \end{bmatrix} \begin{bmatrix} g_{0} \\ g_{1} \\ g_{2} \end{bmatrix}=\begin{bmatrix} r_{0} \\ r_{1} \end{bmatrix}$

如果是一般的矩阵乘法，则需要6次乘法和4次加法，如下：

$r_{0}=(d_{0} \cdot g_{0})+(d_{1} \cdot g_{1})+(d_{2} \cdot g_{2})$

$r_{1}=(d_{1} \cdot g_{0})+(d_{2} \cdot g_{1})+(d_{3} \cdot g_{2})$

但是，卷积运算中输入信号转换成的矩阵不是任意矩阵，其中有规律地分布着大量的重复元素，比如第1行和第2行的$d_{1}$和$d_{2}$，卷积转换成的矩阵乘法比一般矩阵乘法的问题域更小，这就让优化存在了可能。

Winograd是怎么做的呢？

$F(2,3)= \begin{bmatrix} d_{0} & d_{1} & d_{2} \\ d_{1} & d_{2} & d_{3} \end{bmatrix} \begin{bmatrix} g_{0} \\ g_{1} \\ g_{2} \end{bmatrix}=\begin{bmatrix} m_{1}+m_{2}+m_{3} \\ m_{2}-m_{3}-m_{4} \end{bmatrix}$

其中，

$m_{1}=(d_{0}-d_{2})g_{0} \quad m_{2}=(d_{1}+d_{2}) \frac{g_{0}+g_{1}+g_{2}}{2}$

$m_{4}=(d_{1}-d_{3})g_{2} \quad m_{3}=(d_{2}-d_{1}) \frac{g_{0}-g_{1}+g_{2}}{2}$

乍看上去，为了计算

$r_{0}=m_{1}+m_{2}+m_{3}$

$r_{1}=m_{2}-m_{3}-m_{4}$

需要的运算次数分别为：

输入信号$d$

输出$

在神经网络的推理阶段，卷积核上的元素是固定的，因此g

与直接运算的6次乘法和4次加法相比，乘法次数减少，加法次数增加。在计算机中，乘法一般比加法慢，通过减少减法次数，增加少量加法，可以实现加速。

1D winograd

上一节中的计算过程写成矩阵形式如下：

$Y=A^{T}[(Gg) \odot (B^{T}d)]$

其中

$\odot$

为element-wise multiplication（Hadamard product）对应位置相乘，正好，笔者在此突然想起了numpy、tensorflow、pytorch中都有的一个API：爱因斯坦求和，详细请参阅https://www.jianshu.com/p/7a2eb2da0f60

对于二维的卷积：

对于二维情况
numpy.einsum('ij,ij->ij', A, B)
对于三位情况
numpy.einsum('ijk,ijk->ijk', A, B)

回到Winograd算法，

$B^{T}=\begin{bmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 1 & 0 & -1 \end{bmatrix}$

$G=\begin{bmatrix} 1 & 0 & 0 \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ 0 & 0 & 1 \end{bmatrix}$

$A^{T}=\begin{bmatrix} 1 & 1 & 1 & 0 \\ 0 & 1 & -1 & -1 \end{bmatrix}$

$g=[g_{0} \quad g_{1} \quad g_{2}]^{T}$

$d=[d_{0} \quad d_{1} \quad d_{2} \quad d_{3}]^{T}$

$g$:卷积核

$d$:输入

$G$:Filter transform矩阵，尺寸$(m+r-1) \times r$

$B^{T}$:Input transform矩阵，尺寸$(m+r-1) \times (m+r-1)$

$A^{T}$:Output transform矩阵，尺寸$m \times (m+r-1)$

整个计算过程在逻辑上可以分为4步：

Input transform
Filter transform
Hadamar product
Output transform

注意，这里写成矩阵形式，并不意味着实现时要调用矩阵运算的接口，一般直接手写计算过程速度会更快，写成矩阵只是为了数学形式。

1D to 2D，F(2, 3) to F(2x2, 3x3)

上面只是看了1D的一个例子，2D怎么做呢？

论文中一句话带过：

A minimal 1D algorithm F(m, r) is nested with itself to obtain a minimal 2D algorithm,F(m×m, r×r).

$Y=A^{T}[[GgG^{T}]\odot[B^{T}dB]]A$

其中

g：

问题是：怎么nested with itself？

这里继续上面的例子$F(2,3)$，扩展到2D，$F(2 \times 2,3 \times 3)$，先写成矩阵乘法，见下图，图片来自SlideShare，注意数学符号的变化，

将卷积核的元素拉成一列，将输入信号每个滑动窗口中的元素拉成一行。注意图中红线划分成的分块矩阵，每个子矩阵中重复元素的位置与一维时相同，同时重复的子矩阵也和一维时相同，如下所示

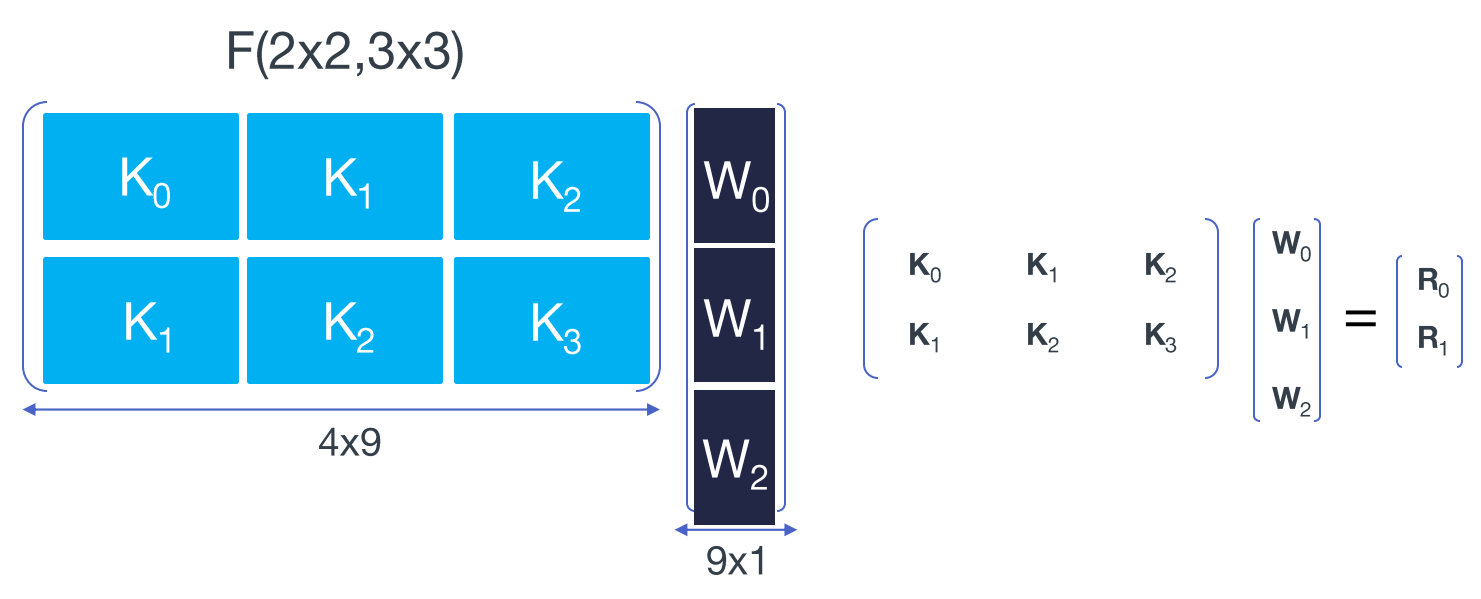
令$D_{0}=[k_{0},k_{1},k_{2},k_{3}]^{T}$，即窗口中的第0行元素，$D_{1} D_{2} D_{3}$表示第1、2、3行；$W_{0}=[\omega_{0},\omega_{1},\omega_{2}]^{T}$，

$$\begin{bmatrix} r_{0} \\ r_{1} \\ r_{2} \\ r_{3} \end{bmatrix}=\begin{bmatrix} R_{0} \\ R_{1} \end{bmatrix}=\begin{bmatrix} K_{0}W_{0}+K_{1}W_{1}+K_{2}W_{2} \\ K_{1}W_{0}+K_{2}W_{1}+K_{3}W_{2} \end{bmatrix}=\begin{bmatrix} A^{T}[(GW_{0})\odot(B^{T}D_{0})]+A^{T}[(GW_{1})\odot(B^{T}D_{1})]+A^{T}[(GW_{2})\odot(B^{T}D_{2})] \\ A^{T}[(GW_{0})\odot(B^{T}D_{1})]+A^{T}[(GW_{1})\odot(B^{T}D_{2})]+A^{T}[(GW_{2})\odot(B^{T}D_{3})] \end{bmatrix}=A^{T}[[G[W_{0} \quad W_{1} \quad W_{2}]G^{T}]\odot[B^{T}[d_{0} \quad d_{1} \quad d_{2} \quad d_{3}]B]]A=A^{T}[[GgG^{T}]\odot[B^{T}dB]]A$$

卷积运算为对应位置相乘再相加，上式中，$A^{T}[(GW_{0}) \odot (B^{T}D_{0})]$表示长度为4的$D_{0}$与长度为3的$W_{0}$卷积结果，结果为长度为2的列向量，其中，$(GW_{0})$和$(B^{T}D_{0})$均为长度为4的列向量，进一步地，$[(GW_{0}) \odot (B^{T}D_{0})+(GW_{1}) \odot (B^{T}D_{1})+(GW_{2}) \odot (B^{T}D_{2})]$可以看成3对长度为4的列向量两两对应位置相乘再相加，结果为长度为4的列向量，也可以看成是4组长度为3的行向量的点积运算，同样，$[(GW_{0}) \odot (B^{T}D_{1})+(GW_{1}) \odot (B^{T}D_{2})+(GW_{2}) \odot (B^{T}D_{3})]$也是4组长度为3的行向量的内积运算，考虑两者的重叠部分$(B^{T}D_{1})$和$(B^{T}D_{2})$，恰好相当于$G[W_{0} \quad W_{1} \quad W_{2}]$的每一行在$B^{T}[d_{0} \quad d_{1} \quad d_{2} \quad d_{3}]$

所谓的nested with itself如下图所示，

此时，Winograd算法的乘法次数为16（上图

卷积神经网络中的Winograd

要将Winograd应用在卷积神经网络中，还需要回答下面两个问题：

上面我们仅仅是针对一个小的image tile，但是在卷积神经网络中，feature map的尺寸可能很大，难道我们要实现
在卷积神经网络中，feature map是3维的，卷积核也是3维的，3D的winograd该怎么做？

第一个问题，在实践中，会将input feature map切分成一个个等大小有重叠的tile，在每个tile上面进行winograd卷积。

第二个问题，3维卷积，相当于逐层做2维卷积，然后将每层对应位置的结果相加，下面我们会看到多个卷积核时更巧妙的做法。

这里直接贴上论文中的算法流程：

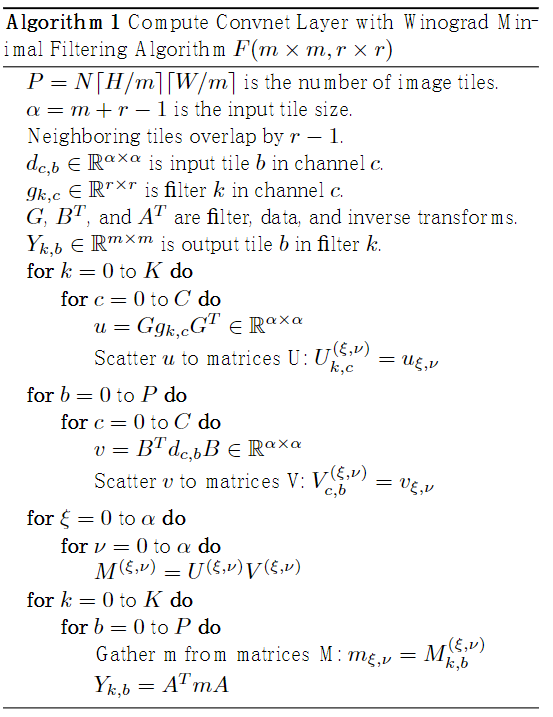
整体仍可分为4步，

Input transform
Filter transform
Batched-GEMM（批量矩阵乘法）
Output transform

算法流程可视化如下，图片出自论文Sparse Winograd Convolutional neural networks on small-scale systolic arrays，与算法对应着仔细推敲还是挺直观的。

注意图中的Matrix Multiplication，对应3维卷积中逐channel卷积后的对应位置求和，相当于$(m+r-1)^{2}$个矩阵乘积，参与乘积的矩阵尺寸分别为$[H/m][W/m] \times C$和$C \times K$，把Channel那一维消掉。

总结

Winograd算法通过减少乘法次数来实现提速，但是加法的数量会相应增加，同时需要额外的transform计算以及存储transform矩阵，随着卷积核和tile的尺寸增大，就需要考虑加法、transform和存储的代价，而且tile越大，transform矩阵越大，计算精度的损失会进一步增加，所以一般Winograd只适用于较小的卷积核和tile（对大尺寸的卷积核，可使用FFT加速，主要是因为现在流行小卷积核，比如1×1、3×3。FFT只有在卷积核超过大约9×9×9的时候，才有速度优势。这是在CPU上用MKL做的测试。不过depth wised conv有取代Winograd的趋势，因为对于1×1、3×3，如果用global depth wised conv的话是不是就体现不出Winograd的优势，这是一个思考点），在目前流行的网络中，小尺寸卷积核是主流，典型实现如$F(6 \times 6,3 \times 3)$
就卷积而言，Winograd算法和FFT类似，都是先通过线性变换将input和filter映射到新的空间，在那个空间里简单运算后，再映射回原空间。
与im2col+GEMM+col2im相比，winograd在划分时使用了更大的tile，就划分方式而言，$F(1 \times 1,r \times r)$