SSD算法精度

论文题目：SSD: Single Shot MultiBox Detector

论文地址：https://arxiv.org/pdf/1512.02325.pdf

大神那年盛夏pytorch复现的SSD算法代码：https://github.com/acm5656/ssd_pytorch

本篇转载于大神荨cecilia的SSD算法思想和结构详解[3]

 

目标检测大方向分主要分为二段式和一段式，前面笔者的博客里说到的RCNN、SSP-Net、Fast RCNN、Faster RCNN军属于二段式，均是利用选择性搜索算法(SS)或者利用backbone CNN获取特征图然后通过region proposal network获取anchor box，然后再分类和回归，“二段”即先得到region proposal，然后再分类回归。

而一段式则是如YOLO、SSD，其主要思路就是均匀地在input image上不同位置进行密集抽样，抽样时可以采用不同尺度和长宽比，然后利用backbone CNN提取特征后直接进行分类和回归，整个过程只需要一步，所以优势在于速度快，但是均匀密集采样的一个重要缺点就是训练比较困难，这主要是因为正样本和负样本极度不均衡，导致模型准确度比较低。

SSD算法(Single Shot MultiBox Detector)，顾名思义，Single shot指明了SSD算法属于one-stage方法，MultiBox指明了SSD是多框预测。对于Faster R-CNN，先通过CNN得到候选框，然后进行分类和回归，而YOLO和SSD可以一步完成检测，YOLO的解读可以参考我之前的一篇文章https://www.cnblogs.com/nanmi/p/12785770.html；相对于YOLO，SSD采用CNN来直接进行检测，而不是像YOLO那样采用全连接层后做检测。相对比于YOLO而言，还有其他两个特点地改变：

第一，SSD提取了不同尺度的特征图来做检测，大尺度特征图可以用来检测小物体，而小特征图用来检测大物体；笔者到这里就笑了，这不是和EfficientNet很相似吗，有特征融合那味儿了。

第二，SSD采用了不同尺度和长宽比的先验框，在faster r-cnn中称为Anchors。YOLO算法缺点是难以检测小物体，而且定位不准，但是对于这几点，SSD在一定程度上克服这些缺点。

  

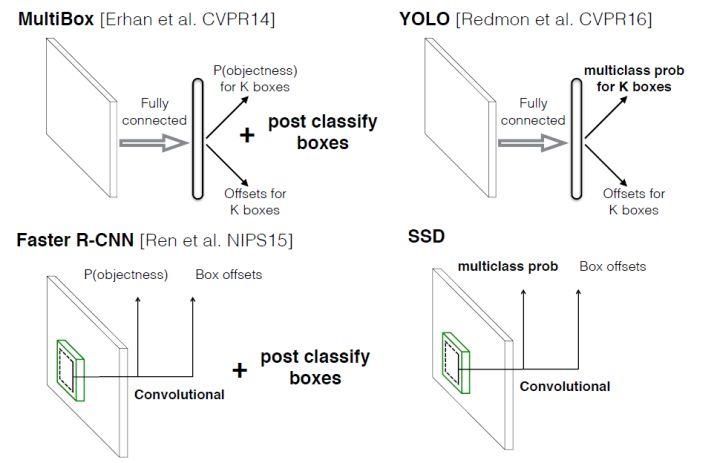
 从上面的图可以看出SSD算法前半部分是vgg-16的架构，作者在vgg-16的层次上，将vgg-16后边两层的全连接层（fc6,fc7）变换为了卷积层，conv7之后的层则是作者自己添加的识别层。

SSD仅在输入图像上运行一个卷积网络并计算特征映射。作者在这个特征映射上运行一个3×3大小的卷积核来预测边界框和分类概率。SSD也使用类似于Faster-RCNN的各种宽高比的anchor boxes ，并学习偏移而不是学习box。为了处理这个尺度，SSD在多个卷积层之后预测边界框。 由于每个卷积层以不同的比例操作，因此能够检测各种比例的目标。

SSD的核心：

• 使用应用于要素图的小卷积滤波器来预测固定的默认边界框的类别得分和框偏移。
• 从不同尺度的特征图中快速检测不同尺度的准确度，并通过纵横比明确区分预测。
• 即使在低分辨率输入图像上，这些设计特征也可实现简单的端到端训练和高精度，从而进一步提高速度与精度之间的权衡。
• 实验包括对PASCAL VOC，COCO和ILSVRC评估的不同输入尺寸的模型进行定时和精度分析，并与一系列最新的最新方法进行比较。

SSD和YOLO一样都是采用一个CNN网络来进行检测，但是SSD却采用了多尺度的特征图，其基本架构图如下：

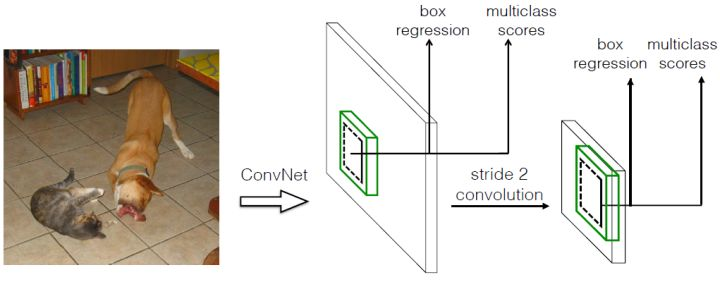
 采用多尺度特征图用于检测

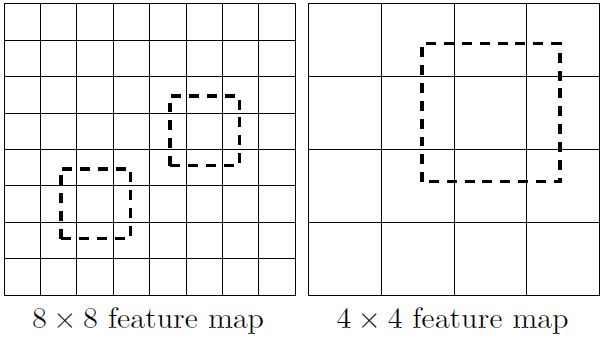
所谓多尺度采用大小不同的特征图，CNN网络一般前面的特征图比较大，后面逐渐采用stride=2的卷积或者pooling层来降低特征图大小。一个比较大的特征图和比较小的特征图都用来做检测，这样做的好处就是比较大的特征图用来检测相对比较小的的目标，而小的特征图负责用来检测大的物体，如图所示：（8x8的特征图可以划分更多的单元，但是其每个单元的先验框尺度比较小。）

 采用卷积做检测

YOLO最后采用的是全连接层，SSD直接采用卷积对不同的特征图进行提取检测结果，对于形状为m×n×p的特征图，只需要采用3×3×p这样小的卷积核得到检测值。

设置先验框

类比于Faster RCNN的先验anchors，在YOLO中，每个单元预测多个边界框，但是都是相对于这个单元本身而言，但是真实目标的形状时多变的，YOLO需要在训练过程中自适应目标的形状。而SSD借鉴了Faster R-CNN中anchors box的原理，每个单元设置尺度或者长宽比不同的先验框，预测的边界框都是以先验框为基准，在一定程度上减少了训练难度。一般情况下，每个单元会设置多个先验框，其尺度和长宽比存在差异。每个单元使用了4个不同的先验框。

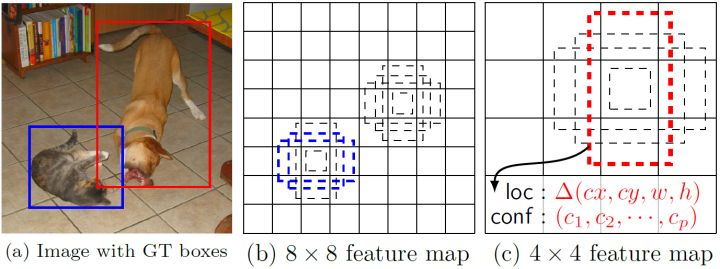
  对于每个单元的每个先验框，其都输出一套独立的检测值，对应一个边界框，主要分为两个部分。第一部分是各个类别的置信度或者评分，值得注意的是SSD将背景也当做了一个特殊的类别，如果检测目标共有 c 个类别，SSD其实需要预测 c+1 个类别的置信度值，其中第一个置信度指的是不含目标或者属于背景的评分。后面当我们说 c个类别置信度时，请记住里面包含背景那个特殊的类别，即真实的检测类别只有 c-1个。在预测过程中，置信度最高的那个类别就是边界框所属的类别，特别地，当第一个置信度值最高时，表示边界框中并不包含目标。第二部分就是边界框的location，包含4个值 $(c x, c y, w, h)$，分别表示边界框的中心坐标以及宽高。但是真实预测值其实只是边界框相对于先验框anchors的转换值或者叫偏置值(论文里面说是offset）。先验框位置用 $d=\left(d^{c x}, d^{c y}, d^{w}, d^{h}\right)$表示，其对应边界框用 $b=\left(b^{c x}, b^{c y}, b^{w}, b^{h}\right)$表示，那么边界框的预测值 $l$ 其实是 $b$相对于$d$的转换值：

$l^{c x}=\left(b^{c x}-d^{c x}\right) / d^{w}, l^{c y}=\left(b^{c y}-d^{c y}\right) / d^{h}$

$l^{w}=\log \left(b^{w} / d^{w}\right), l^{h}=\log \left(b^{h} / d^{h}\right)$

习惯上，我们称上面这个过程为边界框的编码（encode），预测时，你需要反向这个过程，即进行解码（decode），从预测值 $l$  中得到边界框的真实位置 $b$ ：

$b^{c x}=d^{w} l^{c x}+d^{c x}, b^{c y}=d^{y} l^{c y}+d^{c y}$

$b^{w}=d^{w} \exp \left(l^{w}\right), b^{h}=d^{h} \exp \left(l^{h}\right)$

然而，在SSD的Caffe源码实现中还有trick，那就是设置variance超参数来调整检测值，通过bool参数variance_encoded_in_target来控制两种模式，当其为True时，表示variance被包含在预测值中，就是上面那种情况。但是如果是False（大部分采用这种方式，训练可能更容易），就需要手动设置超参数variance，用来对$l$的4个值进行放缩，此时边界框需要这样解码：

$b^{c x}=d^{w}\left(\right.$variance $\left.[0] * l^{c x}\right)+d^{c x}, b^{c y}=d^{y}\left(\right.$variance $\left.[1] * l^{c y}\right)+d^{c y}$

$b^{w}=d^{w} \exp \left(\right.$variance $\left.[2] * l^{w}\right), b^{h}=d^{h} \exp \left(\right.$variance $\left.[3] * l^{h}\right)$

综上所述，对于一个大小m×n的特征图，共有mn个单元，每个单元设置的先验框数目记为 k ，那么每个单元共需要(c+4)×k个预测值，所有的单元共需要(c+4)×kmn个预测值，由于SSD采用卷积做检测，所以就需要(c+4)×k个卷积核完成这个特征图的检测过程。

 

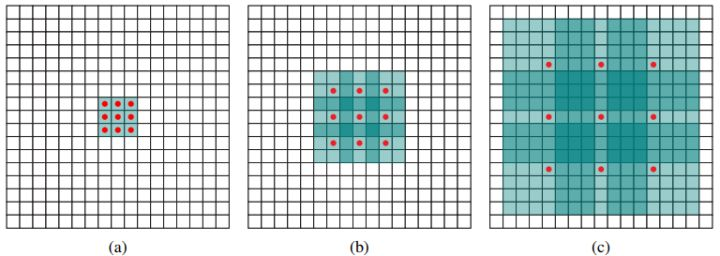
采用VGG16做基础模型，首先VGG16是在ILSVRC CLS-LOC数据集预训练。然后借鉴了DeepLab-LargeFOV，分别将VGG16的全连接层fc6和fc7转换成3×3卷积层 conv6和1×1卷积层conv7，同时将池化层pool5由原来的stride=2的2×2变成stride=1的 3×3（猜想是不想reduce特征图大小），为了配合这种变化，采用了一种Atrous Algorithm，其实就是conv6采用空洞卷积或扩展卷积或带孔卷积（Dilation Conv），其在不增加参数与模型复杂度的条件下指数级扩大卷积的视野，其使用扩张率(dilation rate)参数，来表示扩张的大小，如下图6所示，(a)是普通的 3×3 卷积，其视野就是 3×3 ，(b)是扩张率为2，此时视野变成 7×7 ，(c)扩张率为4时，视野扩大为 15×15 ，但是视野的特征更稀疏了。Conv6采用 3×3 大小但dilation rate=6的扩展卷积。

 然后移除dropout层和fc8层，并新增一系列卷积层，在检测数据集上做finetuing。

其中VGG16中的Conv4_3层将作为用于检测的第一个特征图。conv4_3层特征图大小是 38×38，但是该层比较靠前，其norm较大，所以在其后面增加了一个L2 Normalization层，以保证和后面的检测层差异不是很大，这个和Batch Normalization层不太一样，其仅仅是对每个像素点在channle维度做归一化，而Batch Normalization层是在[batch_size, width, height]三个维度上做归一化。归一化后一般设置一个可训练的放缩变量gamma。

 从后面新增的卷积层中提取Conv7，Conv8_2，Conv9_2，Conv10_2，Conv11_2作为检测所用的特征图，加上Conv4_3层，共提取了6个特征图，其大小分别是(38,38),(19,19),(10,10),(5,5),(3,3),(1,1)，但是不同特征图设置的先验框数目不同（同一个特征图上每个单元设置的先验框是相同的，这里的数目指的是一个单元的先验框数目）。先验框的设置，包括尺度（或者说大小）和长宽比两个方面。对于先验框的尺度，其遵守一个线性递增规则：随着特征图大小降低，先验框尺度线性增加：

$s_{k}=s_{\min }+\frac{s_{\max }-s_{\min }}{m-1}(k-1), k \in[1, m]$

其中m指的特征图个数，但却是5，因为第一层（Conv4_3层）是单独设置的， $\boldsymbol{s}_{k}$表示先验框大小相对于图片的比例，而 $s_{\min }$和$s_{\max }$表示比例的最小值与最大值，paper里面取0.2和0.9。对于第一个特征图，其先验框的尺度比例一般设置为 $s_{\min }$的一半0.1 ，那么尺度为 300×0.1=30。对于后面的特征图，先验框尺度按照上面公式线性增加，但是先将尺度比例先扩大100倍，此时增长步长为 $\left\lfloor\frac{\left\lfloor s_{\max } \times 100\right\rfloor-\left\lfloor s_{\min } \times 100\right\rfloor}{m-1}\right\rfloor=17$，这样各个特征图的 $\boldsymbol{s}_{k}$为20，37，54，71，88 ，将这些比例除以100，然后再乘以图片大小，可以得到各个特征图的尺度为60，111，162，213，264 ，这种计算方式是参考SSD的Caffe源码。综上，可以得到各个特征图的先验框尺度30，60，111，162，213，264 。对于长宽比，一般选取 $a_{r} \in\left\{1,2,3, \frac{1}{2}, \frac{1}{3}\right\}$，对于特定的长宽比，按如下公式计算先验框的宽度与高度（后面的$s_{k}$均指的是先验框实际尺度，而不是尺度比例）：

$w_{k}^{a}=s_{k} \sqrt{a_{r}}, h_{k}^{a}=s_{k} / \sqrt{a_{r}}$

默认情况下，每个特征图会有一个 $a_{r}$=1且尺度为 $\boldsymbol{s}_{k}$的先验框，除此之外，还会设置一个尺度为 $s_{k}^{\prime}=\sqrt{s_{k} s_{k+1}}$且 $a_{r}$=1的先验框，这样每个特征图都设置了两个长宽比为1但大小不同的正方形先验框。注意最后一个特征图需要参考一个虚拟$s_{m+1}$=300×105/100=315来计算 $s_{m}^{\prime}$。因此，每个特征图一共有6个先验框 $\left\{1,2,3, \frac{1}{2}, \frac{1}{3}, 1^{\prime}\right\}$，但是在实现时，Conv4_3，Conv10_2和Conv11_2层仅使用4个先验框，它们不使用长宽比为3,$\frac{1}{3}$的先验框。每个单元的先验框的中心点分布在各个单元的中心，即($\frac{i+0.5} {\left|f_{k}\right|}$, $\frac{j+0.5} {\left|f_{k}\right|}$),i,j属于（0, $\left|f_{k}\right|$），其中 $\left|f_{k}\right|$为特征图的大小。

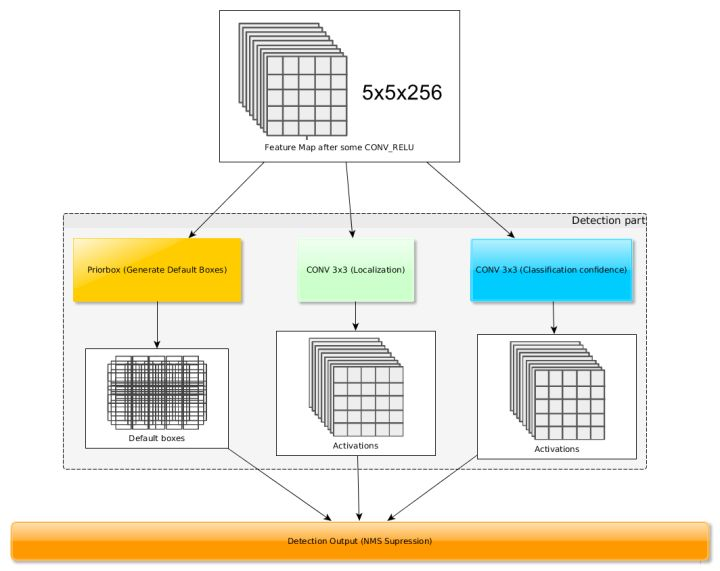
得到了特征图之后，需要对特征图进行卷积得到检测结果，图7给出了一个 5×5大小的特征图的检测过程。其中Priorbox是得到先验框，前面已经介绍了生成规则。检测值包含两个部分：类别置信度和边界框位置，各采用一次 3×3卷积来进行完成。令 $n_{k}$为该特征图所采用的先验框数目，那么类别置信度需要的卷积核数量为$n_{k}$×c，而边界框位置需要的卷积核数量为$n_{k}$×4。由于每个先验框都会预测一个边界框，所以SSD300一共可以预测 38×38×4+19×19×6+10×10×6+5×5×6+3×3×4+1×1×4=8732个边界框，这是一个相当庞大的数字，所以说SSD本质上是密集采样。

1. 训练

先验框匹配

在训练过程中，首先要确定训练图片中的ground truth（真实目标）与哪个先验框来进行匹配，与之匹配的先验框所对应的边界框将负责预测它。在Yolo中，ground truth的中心落在哪个单元格，该单元格中与其IOU最大的边界框负责预测它。但是在SSD中却完全不一样，SSD的先验框与ground truth的匹配原则主要有两点。首先，对于图片中每个ground truth，找到与其IOU最大的先验框，该先验框与其匹配，这样，可以保证每个ground truth一定与某个先验框匹配。通常称与ground truth匹配的先验框为正样本（其实应该是先验框对应的预测box，不过由于是一一对应的就这样称呼了），反之，若一个先验框没有与任何ground truth进行匹配，那么该先验框只能与背景匹配，就是负样本。一个图片中ground truth是非常少的， 而先验框却很多，如果仅按第一个原则匹配，很多先验框会是负样本，正负样本极其不平衡，所以需要第二个原则。第二个原则是：对于剩余的未匹配先验框，若某个ground truth的 IOU大于某个阈值（一般是0.5），那么该先验框也与这个ground truth进行匹配。这意味着某个ground truth可能与多个先验框匹配，这是可以的。但是反过来却不可以，因为一个先验框只能匹配一个ground truth，如果多个ground truth与某个先验框 IOU大于阈值，那么先验框只与IOU最大的那个先验框进行匹配。第二个原则一定在第一个原则之后进行，仔细考虑一下这种情况，如果某个ground truth所对应最大 IOU小于阈值，并且所匹配的先验框却与另外一个ground truth的 IOU大于阈值，那么该先验框应该匹配谁，答案应该是前者，首先要确保某个ground truth一定有一个先验框与之匹配。但是，这种情况我觉得基本上是不存在的。由于先验框很多，某个ground truth的最大 IOU肯定大于阈值，所以可能只实施第二个原则既可以了，这里的TensorFlow版本就是只实施了第二个原则，但是这里的Pytorch两个原则都实施了。图8为一个匹配示意图，其中绿色的GT是ground truth，红色为先验框，FP表示负样本，TP表示正样本。

损失函数

训练样本确定了，然后就是损失函数了。损失函数定义为位置误差（locatization loss， loc）与置信度误差（confidence loss, conf）的加权和：

$L(x, c, l, g)=\frac{1}{N}\left(L_{c o n f}(x, c)+\alpha L_{l o c}(x, l, g)\right)$

其中 $N$是先验框的正样本数量。这里 $x_{i j}^{p} \in\{1,0\}$为一个指示参数，当 $x_{i j}^{p}=1$时表示第 $i$个先验框与第 $j$ 个ground truth匹配，并且ground truth的类别为 $p$ 。 $c$ 为类别置信度预测值。 $l$为先验框的所对应边界框的位置预测值，而 $g$ 是ground truth的位置参数。对于位置误差，其采用Smooth L1 loss，定义如下：

$L_{l o c}(x, l, g)=\sum_{i \in \operatorname{Pos} m \in\{c x, c y, w, h\}}^{N} x_{i j}^{k} \operatorname{smooth}_{\mathrm{L} 1}\left(l_{i}^{m}-\hat{g}_{j}^{m}\right)$

$\hat{g}_{j}^{c x}=\left(g_{j}^{c x}-d_{i}^{c x}\right) / d_{i}^{w} \quad \hat{g}_{j}^{c y}=\left(g_{j}^{c y}-d_{i}^{c y}\right) / d_{i}^{h}$

$\hat{g}_{j}^{w}=\log \left(\frac{g_{j}^{w}}{d_{i}^{w}}\right) \quad \hat{g}_{j}^{h}=\log \left(\frac{g_{j}^{h}}{d_{i}^{h}}\right)$

$\operatorname{smooth}_{L_{1}}(x)=\left\{\begin{array}{ll}0.5 x^{2} & \text { if }|x|<1 \\ |x|-0.5 & \text { otherwise }\end{array}\right.$

由于 $x_{i j}^{p}$ 的存在，所以位置误差仅针对正样本进行计算。值得注意的是，要先对ground truth的 $g$ 进行编码得到 $\hat{g}$ ，因为预测值$l$也是编码值，若设置variance_encoded_in_target=True，编码时要加上variance：

$\hat{g}_{j}^{c x}=\left(g_{j}^{c x}-d_{i}^{c x}\right) / d_{i}^{w} /$variance$[0], \hat{g}_{j}^{c y}=\left(g_{j}^{c y}-d_{i}^{c y}\right) / d_{i}^{h} /$variance[1]

$\hat{g}_{j}^{w}=\log \left(g_{j}^{w} / d_{i}^{w}\right) /$variance$[2], \hat{g}_{j}^{h}=\log \left(g_{j}^{h} / d_{i}^{h}\right) /$variance[3]

对于置信度误差，其采用softmax loss:

$L_{\text {conf}}(x, c)=-\sum_{i \in \text {Pos}}^{N} x_{i j}^{p} \log \left(\hat{c}_{i}^{p}\right)-\sum_{i \in N e g} \log \left(\hat{c}_{i}^{0}\right) \quad$ where $\quad \hat{c}_{i}^{p}=\frac{\exp \left(c_{i}^{p}\right)}{\sum_{p} \exp \left(c_{i}^{p}\right)}$

权重系数 $\alpha$ 通过交叉验证设置为1。

数据扩增

采用数据扩增（Data Augmentation）可以提升SSD的性能，主要采用的技术有水平翻转（horizontal flip），随机裁剪加颜色扭曲（random crop & color distortion），随机采集块域（Randomly sample a patch）（获取小目标训练样本），如下图所示：

 

 

 预测过程

预测过程比较简单，对于每个预测框，首先根据类别置信度确定其类别（置信度最大者）与置信度值，并过滤掉属于背景的预测框。然后根据置信度阈值（如0.5）过滤掉阈值较低的预测框。对于留下的预测框进行解码，根据先验框得到其真实的位置参数（解码后一般还需要做clip，防止预测框位置超出图片）。解码之后，一般需要根据置信度进行降序排列，然后仅保留top-k（如400）个预测框。最后就是进行NMS算法，过滤掉那些重叠度较大的预测框。最后剩余的预测框就是检测结果了。

 

Reference

[1] https://www.cnblogs.com/cmai/p/10076050.html

[2] https://blog.csdn.net/weixin_39749553/article/details/88086486

[3] https://www.cnblogs.com/cecilia-2019/p/11342791.html

[4] http://www.360doc.com/content/20/0104/21/99071_884171814.shtml