Deep Graph Convolutional Networks with Hybrid Normalization for Accurate and Diverse Recommendation
ABSTRACT
- 文章提出GCN基于GCN的模型在浅层就达到了最佳性能,这就没有使用到高阶信号。
- 基于GCN的模型,对于聚合邻域信息使用的是一样的归一化规则,使得邻居的重要性变得同等重要。
但是节点之间有内在的差异,需要使用不同的归一化来聚合邻域信息。这项工作提出了一个新的模型:混合归一化的深度卷积网络(DGCN-HN)。
首先,设计了一个残差连接和整体连接组成的深度图卷机推荐网络,以缓解过平滑问题,允许对GCN进行更深层次的有效训练;
然后提出混合归一化层和简化的注意力网络,通过自适应地融合来自不同归一化规则的信息来灵活建模邻域的重要性;
INTRODUCTION
文章认为目前基于GCN的模型存在两个问题
- 层数不够
- 使用了固定的归一化规则
- left normalization(左归一化),给不同的邻居分配相同的归一化
- symmetric normalization(对称归一化),给流行的邻居分配较小的权重,给不流行的邻居分配较大的权重
使用固定的归一化规则会导致次优的结果,文章从准确度和多样性的角度探索了左归一化和对称归一化的效果。
DGCN-HN使用了residual connection和holistic connection
residual connection:残差链接
holistic connection:整体链接
提出的模型能将图卷积加深至8层。
将左归一化和对称归一化结合,提出一种混合归一化,更灵活的适应邻居重要性。
2 PRELIMINARIES
3 METHOD
DGCN-HN的示意图如下:
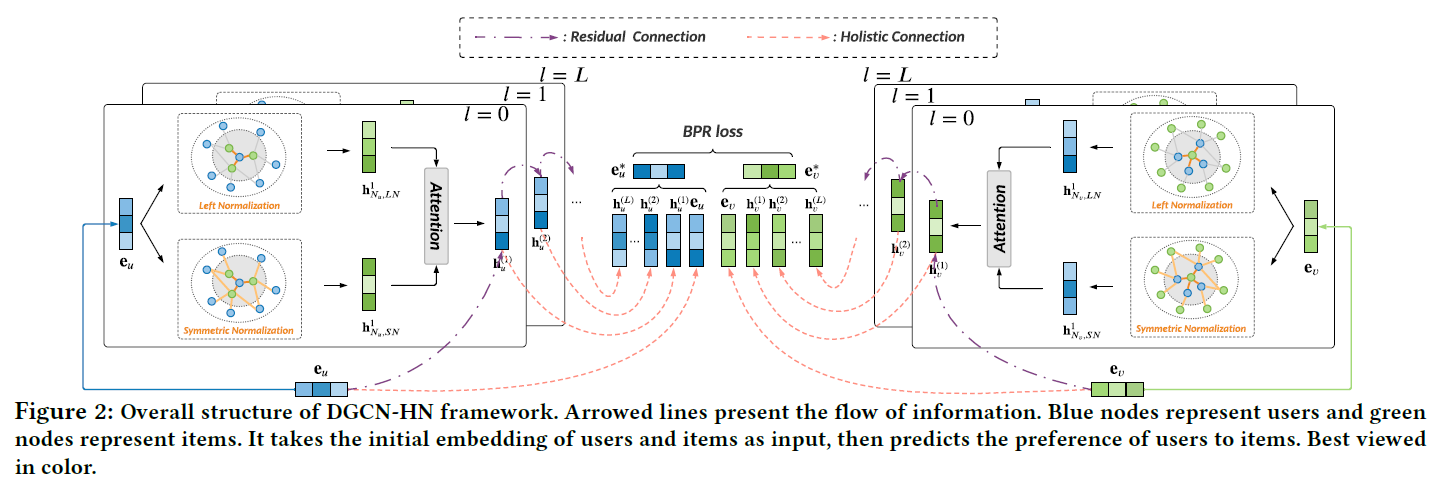
包括三个主要组成:
- 设计了带有残差链接和整体链接的深度图卷积网络推荐
- 引入混合归一化层对邻居重要性进行灵活建模,将左归一化和对称归一化相结合
- 提出一种简化的注意力网络,自适应融合不同归一化方法表示信息
3.1 Embedding Layer
使用embedding来表示用户和项目的节点,而不是使用one-hot向量
3.2 Deep Graph Convolutional Network for Recommendation
用户u和项目v的表示更新公式如下:
DGCN的示意图如下:
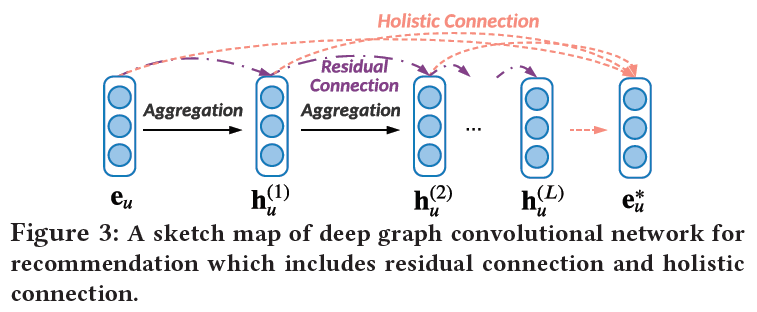
每层的线性聚合可以表示为残差链接,公式如下:
在经过L层的聚合后,使用整体链接把所有层的表示进行整合,公式如下:
模型使用基于元素的平均聚合作为最后一层的融合策略。
3.3 Hybrid Normalization for Flexible Modeling of Neighbor Importance
以用户节点为例
对称归一化的公式如下:
左归一化的公式如下:
简单平均传播
为了结合两种归一化的优点,对这两种队以华应用平均运算,公式如下:
3.4 Simplified Attention Network for Adaptive Combination
\(h_{N_u,LN}^{(l)}\)和\(h_{N_u,SN}^{(l)}\)表示左归一化和对称归一化,以用户节点为例,节点更新公式如下:
其中\(\alpha_{u,*}^l\)表示不同层的归一化注意力分数
计算注意分数时,考虑了两个方面:
- 邻居的自信息
- 中心表示和邻居表示之间的相似性
注意力网络的公式如下:
其中,\(z_{u,*}^{(l+1)}\)是归一化之前的注意力评分,\(W_1^{(l)}\in \mathbb{R}^{1\times d^t},W_2^{(l)}\in \mathbb{R}^{d^t\times d^l}\)是特征变换矩阵,\(\sigma\)是激活函数,\(d^t\)是注意力网络的隐藏层的维数。\(\odot\)表示哈达玛积,对应位置的元素相乘。
经验之谈,去除了特征变换矩阵和激活函数,使用平均聚合,得到简化的注意力网络如下:
之后使用Softmax函数得到\(\alpha\),公式如下:
3.5 Model Training
损失函数为BPR loss
4 EXPERIMENTS
4.1 Experiment Setup
4.1.1 Dataset
- Gowalla
- Yelp2018
- Amazon-Book
4.1.2 Baseline Models - BPRMF
- GCMC
- Pinsage
- NGCF
- ResGCN
- MacridVAE
- DGCF
- Light-GCN
4.1.3 Evaluation Metrics - Recall@k
- NDCG@k
- Coverage@k
- Entropy@k
4.1.4 Parameter Settings
4.2 Accuracy Comparison
下表显示了各种模型的Recall和NDCG对比,k=20
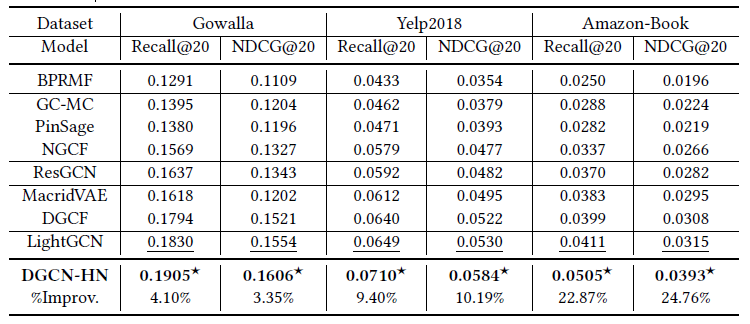
文章还考虑到了推荐结果的多样性,进行了准确度-多样性比较,结果如下图:
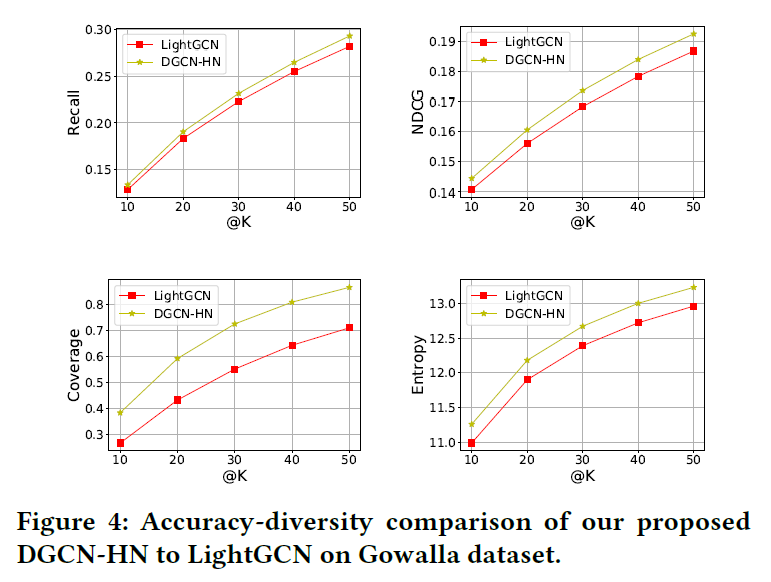
4.4 Ablation and Effectiveness Analysis
下表展示了不同归一化方案的性能比较:
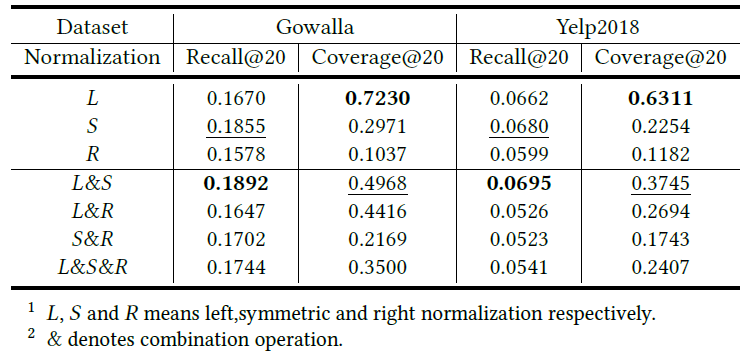
可以看出:
- 使用单一归一化时,左归一化获得最佳分集,对称归一化获得最佳精度,右归一化在各方面表现最差
- 混合归一化中,左归一化和对称归一化的结合获得了最好的精度和多样性
- 综合比较,L&S是最好的
4.4.2 Impact of proposed component
具体实验结果如下表:
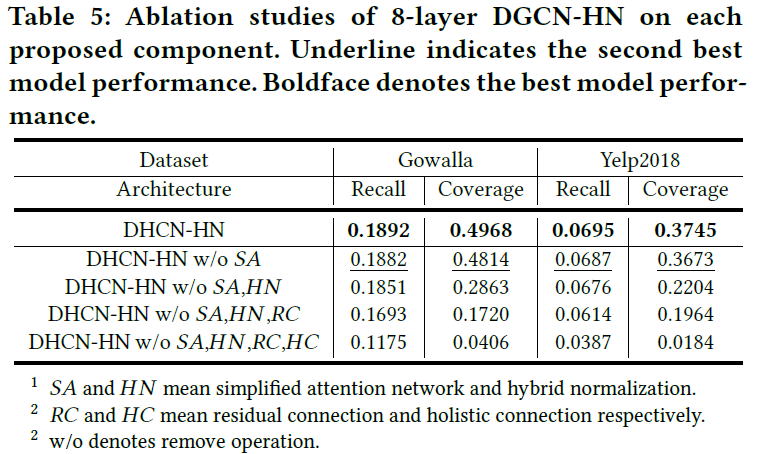
- 四个主要组成部分,包括:
- 简化的注意力网络
- 混合归一化
- 残差链接
- 整体链接
对模型都有效果
- 引入的简化注意力网络提高了准确率,还增加了多样性
- 混合归一化在两个数据集上有显著的性能改善,特别是coverage方面
- 残差链接和整体链接在训练很深的图卷积网络是很重要的
4.4.3 Impact of Network Depth
研究了不同层数的影响,LightGCN-Final表示只使用最后一层的表示用于预测,下图表示了结果:
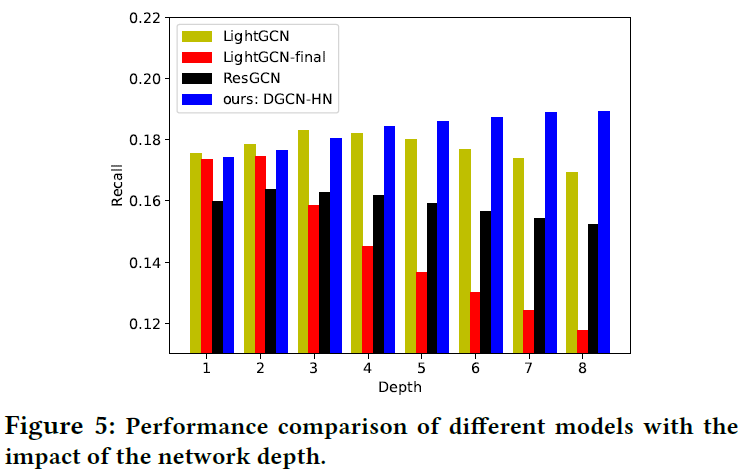
4.5 User Analysis
此部分研究哪类用户更多受益于高阶协助信号,比较了10层DGCN-HN,Light-GCN,LightGCN-Final的性能,结果图如下:
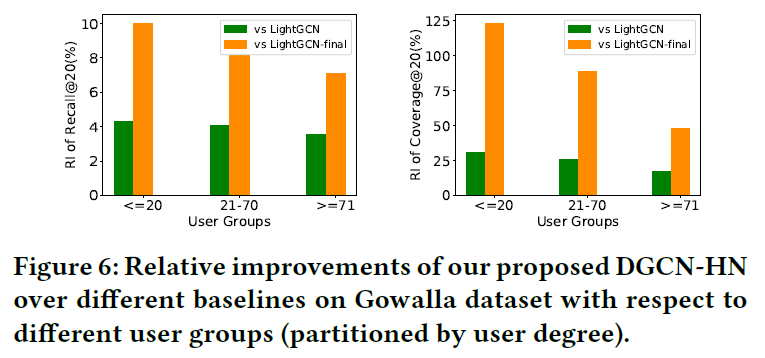
- DGCN-HN在所有用户群上的表现都优于LightGCN-Final和LightGCN
- 交互非常少的稀疏用户的改进更为显著
- 2层的LightGCN-Fianl的改善比3层的LightGCN更大,表明,引入更多的邻居信息可以带来更多的改进。




