Learning User Representations with Hypercuboids for Recommender Systems

ABSTRACT

建模用户兴趣在推荐系统中至关重要。在文章中，作者提出了一种新的用户兴趣表示模型。具体来说，该模型的关键新颖之处在于它将用户兴趣明确地建模为超长方体而不是空间中的一个点。在这个方法中，推荐分数是通过计算用户超长方体和项目之间的组合距离来学习的。这有助于减轻现有协同过滤方法潜在的几何不灵活性，从而实现更好的建模能力。进一步，提出了两种超长方体的两种变体，以增强捕获用户兴趣多样性的能力。还提出一种神经架构，通过捕获用户的活动序列(例如：购买和评价)，来租金用户超长方体学习。作者通过对公共和商业数据集的广泛实验证明了模型的有效性。实验取得了soat效果。

INTRODUCTION

文章提出的新的超长方体推荐方法，超长方体（也成为超矩形）是将3维长方体推广到4维或者更多维。更具体地说，使用富有表现力的超长方体来表示用户，已捕获用户的复杂多样的兴趣。推荐是基于用户超长方体和项目之间的关系作出的。

常见的用户建模方法旨在将用户表示为向量空间中的点。例如，标准分解模型将大型交互矩阵分解为低维空间中的用户和项目潜在嵌入向量。结果，推荐被简化为识别在该空间中与用户接近或相似的项目。但是这存在不足：

• 将不同的、多样性的兴趣用单个点的嵌入表示是有问题的，直观上，用户对不同类别或领域的项目有不同的品味和考虑。
• 对于大多数因素，用户有偏好的范围分布。例如，消费者通常有他们可接受的价格范围。用单个值对这样的范围进行建模是没有表现力的。
  显然，这样的系统在几何上是有限制的，因此提出了一个更丰富的潜在表示系统来克服这些限制。这种将用户表示为超长方体的新范式，超越了点嵌入表示，可以更有效地捕捉用户错综复杂的兴趣。超长方体是一个包含无数点的子空间，比单个点具有更多的表示能力。此外，每个因素的偏好范围可以自然地用超长方体的边缘建模。

总的来说，基本思想：对于每个用户，学习单个或多个超长方体来代表用户的兴趣。用户超长方体和项目点之间的关系是通过重新设计的距离度量来捕获的，其中考虑了超长方体外部和内部的距离，理想情况下，用户超长方体将允许更大程度的灵活性和表现力。

THE PROPOSED METHOD

设有一组用户，\(u\in \{1,\ldots,|U|\}\)，一组项目，\(i \in \{1,\ldots,|I|\}\)。目标是在给定现有反馈的情况下，为用户生成一组可推荐的项目，通常是隐式反馈，例如：点击、购买、喜欢。如果用户u和项目i存在交互，将\(y_{ui}\)设置为1，否则为0，且\(y_{ui}\)是交互矩阵\(Y\in R^{|U|\times |I|}\)的一个条目。

2.1 Representing Users as Hypercuboids

为了计算方便，定义了一个具有中心和偏移量的超长方体，两者具有相同的维度。具体地，在\(\mathbb{R}^d\)上进行操作，让\(c\in \mathbb{R}^d\)代表超长方体的中心，\(f\in \mathbb{R}_{0+}^{d}\)表示非负偏移。偏移用于确定超长方体的边缘长度，具体定义如下：

\[Hypercuboid \equiv \{p\in \mathbb{R}^d:c-f \preceq p \preceq c+f\} \]

其中，p表示在超长方体中的点。每个用户都使用超长方体来表示，使用\(C\in R^{|U|\times d}\)和\(F\in R_{0+}^{|U|\times d}\)来表示所有用户的中心和偏移。因此，用户u可以被表示为\(usr_u(C_u,F_u)\)。项目用点来表示，并且用\(V\in R^{|I|\times d}\)来表示。显然，项目点可以在用户超长方体的外部、内部或者表面上。因此，需要一种合适的方法来评估用户好项目之间的关系。同时应该保留超长方体的特性。

为了实现这一点，采用点到超长方体的距离的复合。由外部距离和内部距离组成，首先在超长方体表面上找到离item最近的点，表达式如下：

\[p_{ui}=min(p_u^{max},max(p_u^{min},V_i)) \]

其中，\(p_u^{max}\)和\(p_u^{min}\)表示超长方体的右上角和左下角，他们的正式定义如下：

\[p_u^{max}=C_u+F_u \\ p_u^{min}=C_u-F_u \]

很显然，\(p_{ui}\)和用户超长方体和项目嵌入表示都有关联，任何一方的移动都会导致这一点的转变，示意图如下：

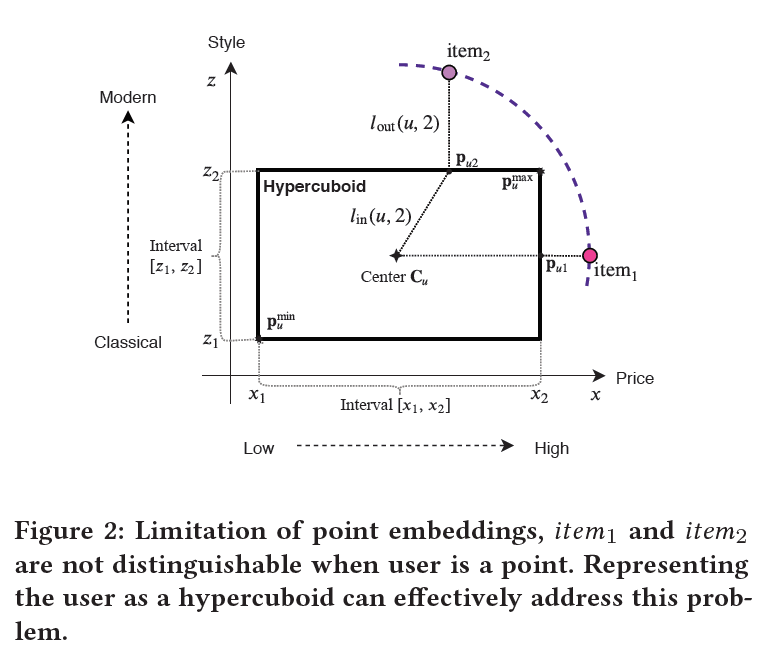
因此，外部距离就是\(p_{ui}\)和\(V_i\)的距离，内部距离就是\(p_{ui}\)和超长方体中心的距离，如下：

\[l_{out}(u,i)=\parallel p_{ui}-V_i\parallel_2^2,\\ l_{in}(u,i)=\parallel p_{ui}-C_u \parallel_2^2 \]

这里使用欧几里得距离，然后将两个距离组合如下来衡量用户-项目关系：

\[l(u,i)=l_{out}(u,i)+\gamma \cdot l_{in}(u,i) \]

这里的系数\(\gamma\)用于控制内部距离的贡献。理论上，如何设置\(\gamma=0\)，如果一个项目位于用户超长方体中，则说明用户对这个项目感兴趣，不会管用户自身的坐标。这能够缓解用户和发生交互行为的项目映射到相同点的情况。

这种模式有两种好处：

• 一个用户超长方体可以被看成一个包括了无数项目点的集合，这意味着它可以包含用户喜欢的任意数量的项目，而不会丢失太多的信息。
• 提出的组合距离可以克服现有方法采用的直接距离的障碍，组合距离为：\( l(u,i)=l_{out}(u,i)+\gamma \cdot l_{in}(u,i) \)

第二个好处的解释性如下：假设有两个项目位于以\(C_u\)为圆心的圆的圆周上。使用常用的欧几里得距离，系统会得出结论，该用户同样喜欢这两个项目，但是考虑figure2的情况。可以看到，当考虑到超长方体的边缘时，很明显，item1和item2到超长方体的距离不相等。用户可能会对item1更感兴趣。

可以将偏移量视为每个维度中用户偏好的范围，如果x轴表示价格，z轴表示款式，那么明显，用户对款式的容忍度比价格小。因此，即使item2有着更容易接受的价格，但是用户会更喜欢item1，因为item2不是用户喜欢的风格；

同时为了确保用户超长方体里面的项目排名比外面的高，在\(l(u,i)\)加入额外的距离，如下：

\[l_{add}(u,i)=2(\sigma(\alpha \parallel p_{ui}-V_i\parallel _2^2)-\frac{1}{2})\parallel F_u \parallel _2^2 \]

其中\(\alpha\)是设置大于100的值，\(\sigma\)是sigma激活函数。当项目在超长方体内时，该距离为0，否则，它大约大于超长方体的最大对角线长度的一半。

2.2 Variants of Hypercuboids

此部分介绍两种超长方体的变体，原理是生成多个超长方体，每个超长方体为用户兴趣提供不同的视图。可以提高捕获用户兴趣多样性的能力。下图展示了两种变体：

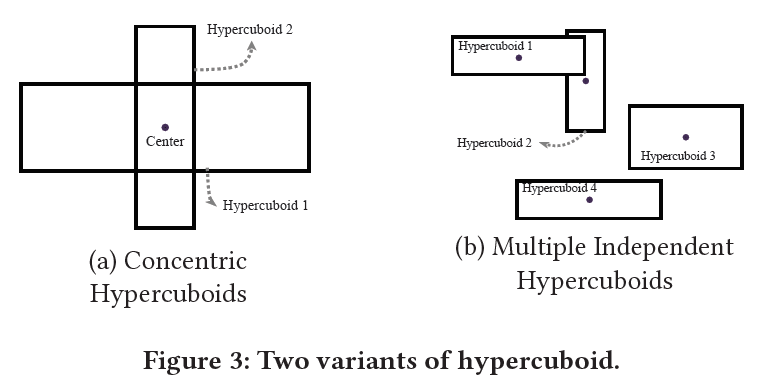
2.2.1 Concentric Hypercuboids

使用多个同心超长方体来表示每个用户，添加几个偏移，并保持中心不变。

同心超长方体不仅可以将规则超长方体扩展到不规则空间，还可以缓解上述的问题。设想有M个偏移，每个超长方体有两个距离，将他们聚合得到最终距离表示，如下：

\[l(u,i)=\sum_{j=1}^{M}l_{out}^j(u,i)+\gamma\cdot min(l_{in}^1(u,i),\ldots,l_{in}^M(u,i)) \]

上述公式，所有的外部距离都被相加，但只使用最小的内部距离。目的是为了弱化内部距离的影响；

2.2.2 Multiple Independent Hypercuboids

为了进一步增强不同兴趣进行建模的能力，还可以使用具有不同中心和偏移的多个超长方体，最终的距离函数定义如下：

\[l(u,i)=min(l^1(u,i),\ldots,l^M(u,i)) \]

至于加法距离，可以取所有超长方体的最大additional距离。(additional distances定义为：\(l_{add}(u,i)=2(\sigma(\alpha \parallel p_{ui}-V_i\parallel _2^2)-\frac{1}{2})\parallel F_u \parallel _2^2\))

2.3 Learning the Centers and Offsets

用户会与很多的项目发生交互行为，文章使用最后L个交互来预测下一个推荐项目。嵌入矩阵\(S_u^{(t)}\in \mathbb{R}^{L\times d}\)，这代表在时间步t的L个项目的表示。可以通过整体项目嵌入表示矩阵V和索引L来获得。

文章使用由双向LSTM堆叠的神经网络和自注意力机制，来捕获用户的兴趣（偏移）

\[S^{'}=Bi-LSTM(S_u^{(t)}) \]

双向LSTM是用来加强序列表示能力，注意力机制如下：

\[a_u^{(t)}=softmax(\frac{f(S^{'})\cdot f(S^{'})^\top }{\sqrt{d}})\cdot S_u^{(t)} \]

其中\(a\in \mathbb{R}^{L\times d}\)是当前序列的变换表示；f是非线性层；然后被传入一个池化层得到一个d维的向量：

\[s_u^{(t)}=pooling(a_u^{(t)}) \]

这里的池化层可以是平均池化，最大值池化，最小值池化，求和池化；可以用\(s_u^{(t)}\)表示中心或者偏移，或者同时表示两者；

此外，超长方体的偏移通常需要记住大量的信息。例如，要获得价格区间，需要存储用户购买的所有商品的价格，以准确推断出用户可接受的价格范围。为此，采用键值记忆网络来执行记忆过程。让\(M\in \mathbb{R}^{d\times N}\)表示记忆，\(K\in \mathbb{R}^{d\times N}\)表示key矩阵，这里的N控制着记忆的大小；

记忆模型的输入是\(s_u^{(t)}\)，，可以从key矩阵中获得key，如下：

\[k=softmax(s_u^{(t)}K) \]

再使用这个key向量k，从记忆矩阵中，选择相关的信息片段，如下：

\[m=k\cdot M^\top \]

使用ReLU函数来包裹所有偏移量，保证得到的值是非负的。对于多个超长方体，可以在中心、偏移量上添加密集层，一次获得多个中心和偏移量，具体如下图所示：

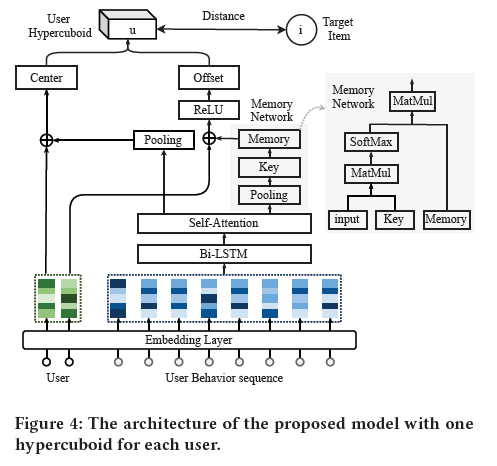
2.4 Optimization

损失函数如下：

\[L=\sum_{(u,i)\in \mathcal{T}^+}\sum_{(u,j)\in \mathcal{T}^-}max(0,\ell (u,i)+\lambda-\ell (u,j)) \]

其中，\(\mathcal{T}^+\)和\(\mathcal{T}^-\)是positive和negative的用户-项目交互对。\(\lambda\)是分隔两个项目的边界。对于正则化，使用了\(L_2\)和dropout。

EXPERIMENTS

3.1 Datasets

使用了四个公开的基准数据集和两个商业数据集，统计信息如下：

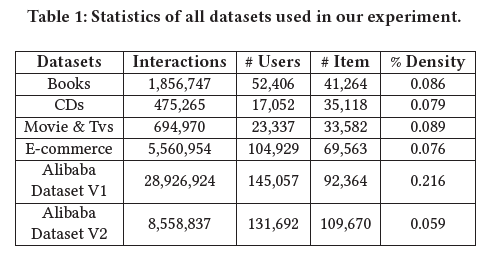
3.2 Evaluation Measures

使用了三个评估指标：

• Recall@k
• NDCG@k
• MAP@k

3.3 Compared Methods

两组方法，如下：

第一组，两个非神经网络推荐方法：

• Matrix Factorization with Bayesian Personalized Ranking(BPRMF)
• Translational Recommender Systems(TransRec)
  第二组，五个神经网络方法：
• YouTubeDNN
• Gated Recurrent Unit for Recommendation(GRU4Rec)
• Convolutional Sequence Embedding Recommendation Model(Caser)
• Self-Attentive Sequential Recommendation(SASRec)
• Hierarchical Gating Networks(HGN)

3.4 Implementation Details

使用tensorflow来实现

3.5 Experimental Results

实验结果的对比如下：

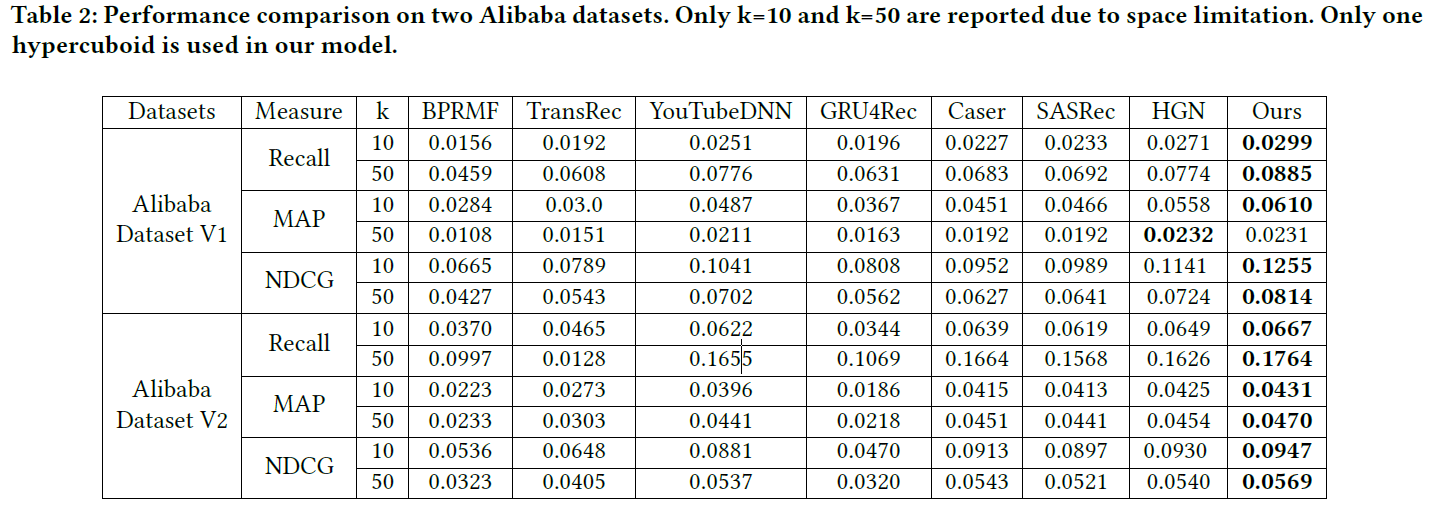
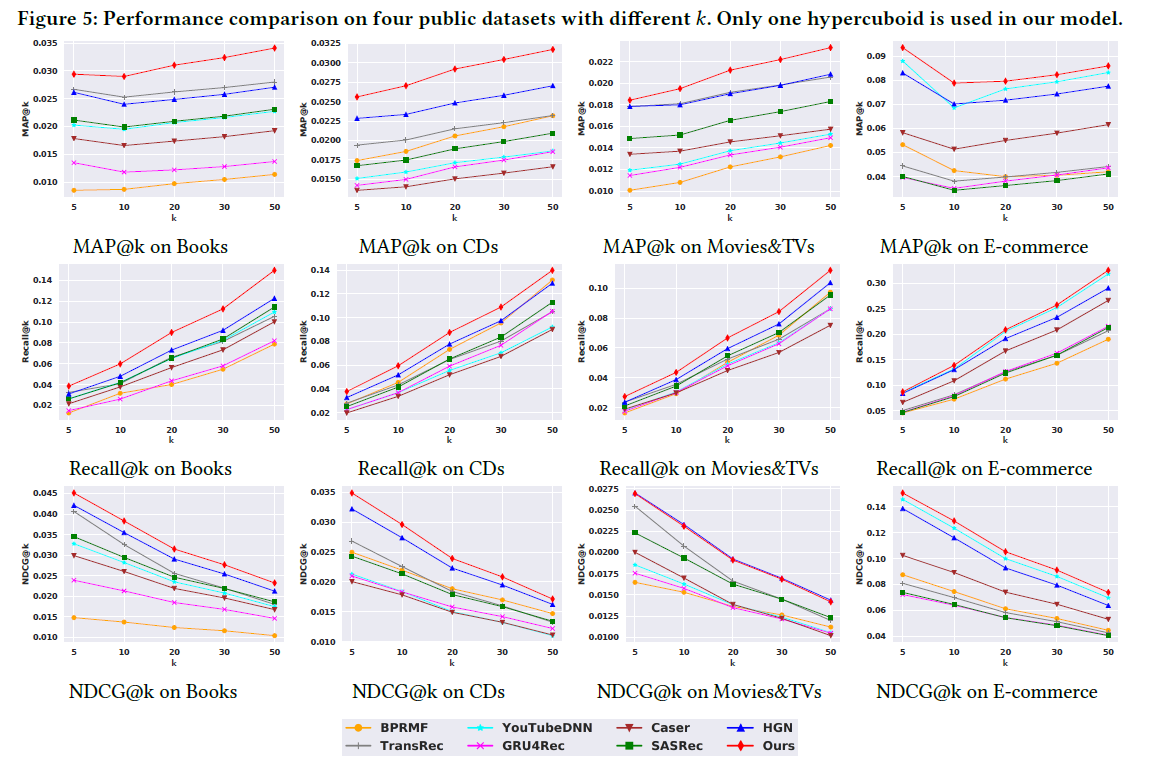
3.6 Adding More Hypercuboids

此部分，验证所提出的超长方体变体的有效性，下表显示了不同数量的超长方体的性能：

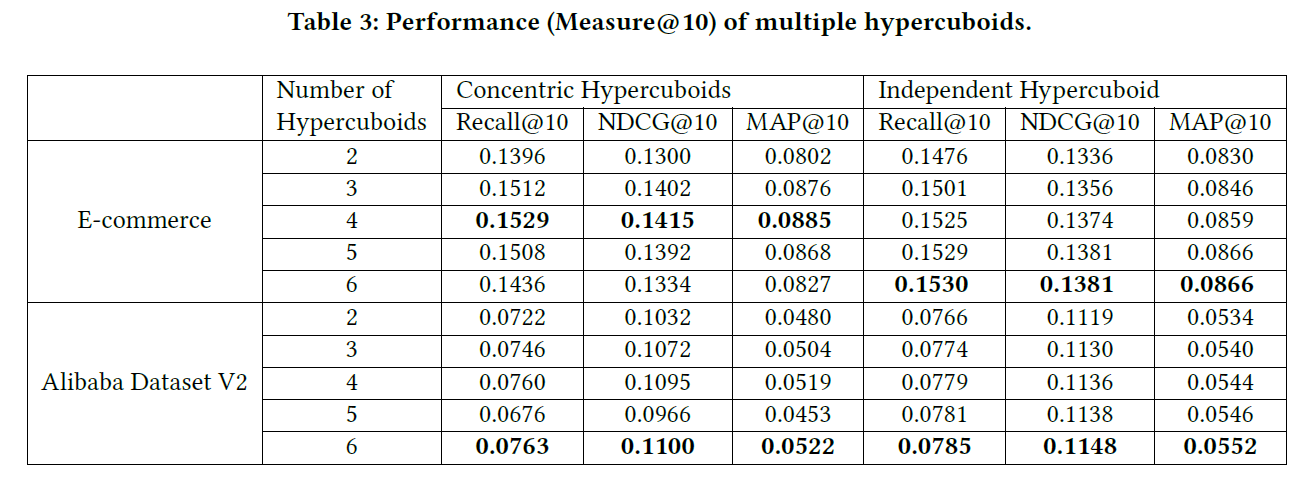
可以看出，添加更多的超长方体可以提高模型的性能。表中的结果看出，使用4-6个超长方体可以带来令人满意的结果。但是8-10个超长方体，性能会下降。

3.7 Using Hypercuboids Only

此部分研究神经架构对模型性能的影响。为此，用简单平均池化替换所有神经架构，具体结果如下：

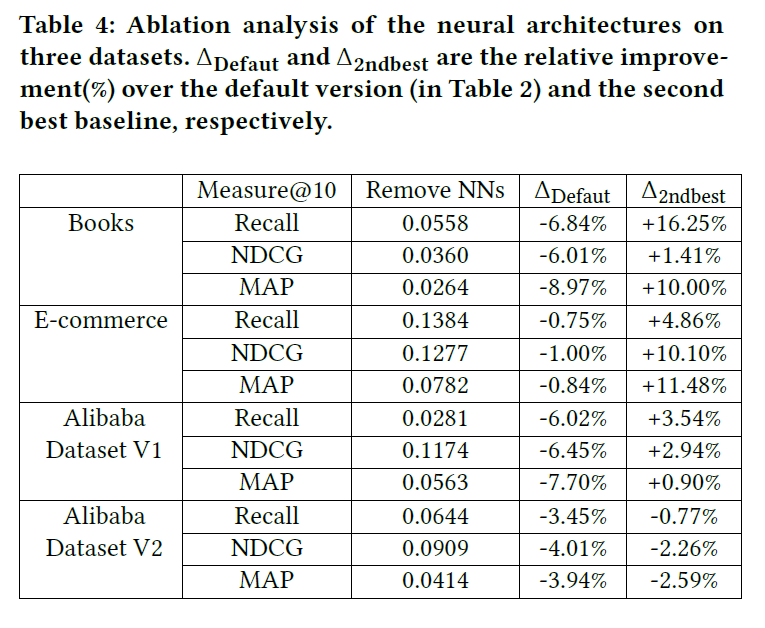
3.8 Sensitivity of Hyper-parameters

3.8.1 Embedding Size

下图中的(a),(b),(c)分析了嵌入表示大小的影响。很明显，增加嵌入大小可以提高性能，本文的模型维度大小应该设置为不小于100；

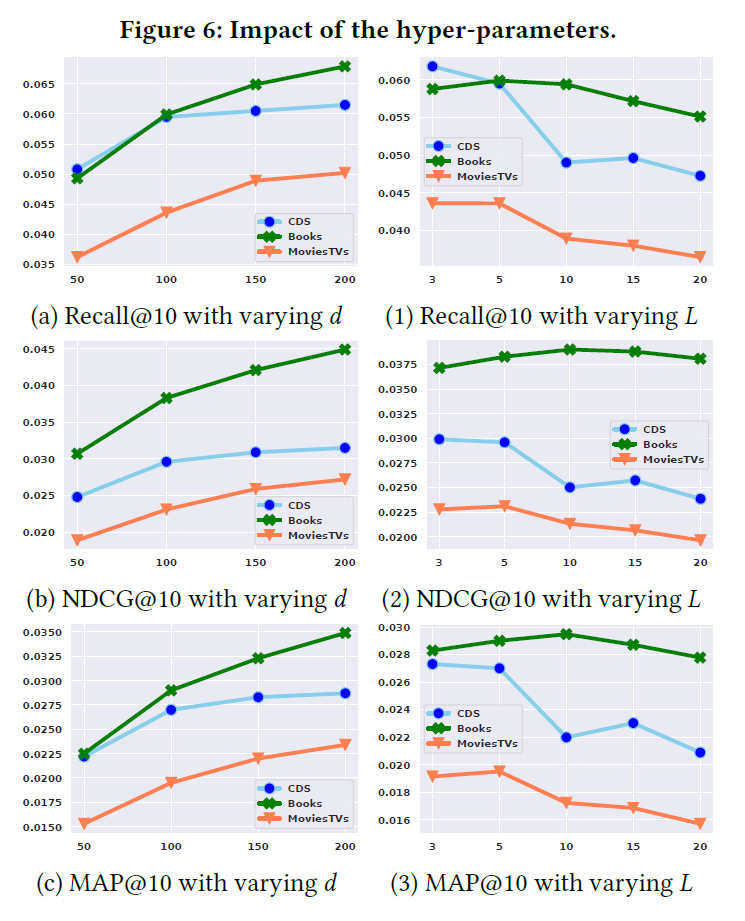
3.8.2 Sequence length

上图中的(1),(2),(3)分析了序列长度L的影响。可以看到模型在CDs和Movies&TVs上，短序列的效果更好。而在Books数据集上，结果更为稳定；

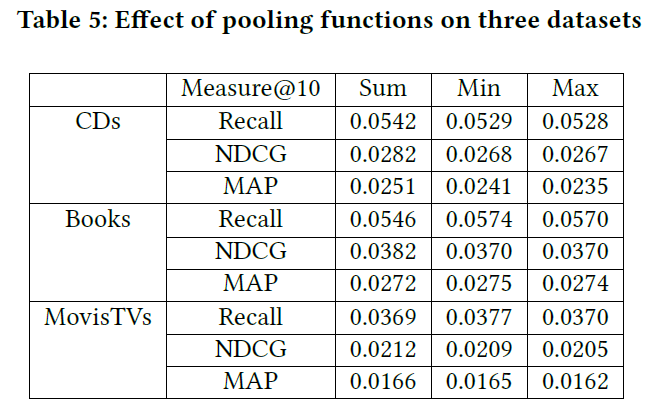
3.8.3 Pooling Function

下表展示了，不同池化函数的效果，三种池化函数(sum, min, max pooling)都会导致在三个数据集上平均池化的退化。

3.9 Visualization of User Hypercuboids and Item Embeddings

可视化结果如图所示：

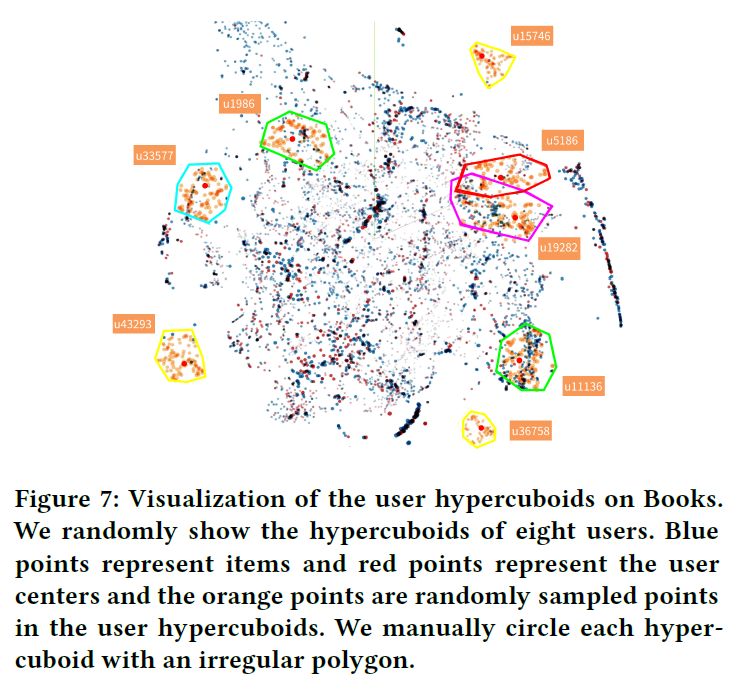
将3000个item和3000个user中心，投影成一个3维空间。然后随机选择8个用户，对于每个用户，在超长方体中均匀采样100个点并将它们投影到同一个空间。可以看出，模型可以成功地学习到不同尺寸和位置的超长方体来表示用户。位于超长方体内部的项目更可能被推荐给用户。同时，用户之间的交互也能很好地可视化。

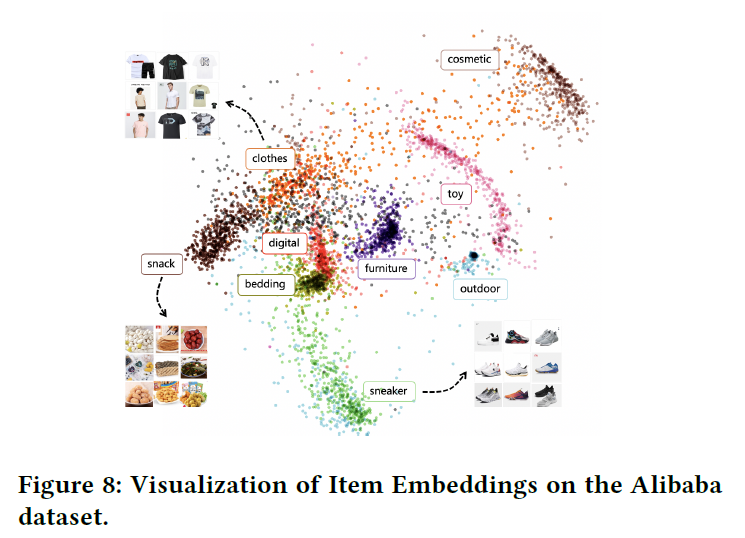
此外，模型能够很好地学习项目的表示。将company数据集(V1)投影到2维空间中，如下图所示，可以观察到来自不同类别的物品被分开了，相关类别的物品会更接近。

3.10 Case Study with Multiple Hypercuboids

从数据集中随机选取一个用户，使用三个独立的超长方体，结果如图所示：

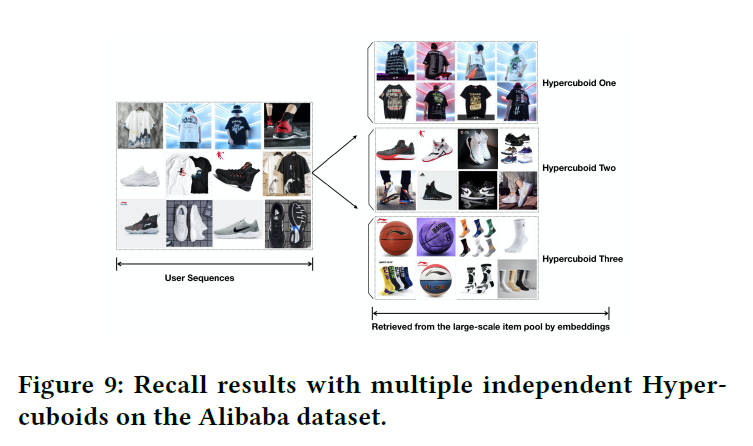
• 找回项目与对应的用户序列强相关
• 不同的超长方体可以捕获历史序列中兴趣的不同方面，例如：T恤，运动鞋
• 单个超长方体还可以从密切相关的类别种召回一组不同的项目。例如，超长方体3既能会议袜子，也能回忆篮球。显然，模型适合捕获用户的不同兴趣。