Bipartite Graph Embedding via Mutual Information Maximization

BiGI

ABSTRACT

二部图的嵌入表示近来引起了人们的大量关注。但是之前的大多数方法采用基于随机游走或基于重构的目标，这些方法对于学习局部图结构通常很有效。

文章提出：二部图的全局性质，包括同质节点的社区结构和异质节点的长期依赖关系，都没有得到很好的保留。因此文章提出二部图嵌入表示，称为BiGI，通过引入一个新的local-global infomax目标，来捕捉全局属性。BiGI首先生成一个全局表示，该表示由两个原型表示组成。然后，BiGI通过子图级别的注意力机制将采样的边encode成局部表示。通过最大化局部表示和全局表示的mutual information，使得二部图中的节点具有全局相关性。

文章在不同的基准数据集上进行实验，目标为top-K和链接预测任务。

---

INTRODUCTION

最近在图嵌入表示取得了很大的进展，虽然很多工作在同构和异构图都能很好的工作，但是他们都不是为二部图量身定做的。因此学习二部图的嵌入表示是次优的。

为了解决这个问题，有许多专门的研究，大致分为两类：基于随机游走和基于重启方法。

• 基于随机游走：依赖于随机行走的启发式算法来生成不同的节点序列。

• 基于重启：通过预测滑动窗口内的上下文节点来学习节点表示。基于重启的方法与协同过滤密切相关。它们试图通过学习不同的编码器来重建邻接矩阵，特别的，一些工作训练图神经网络，通过递归的聚集邻域节点的特征来学习节点表示。

• 举个例子
  

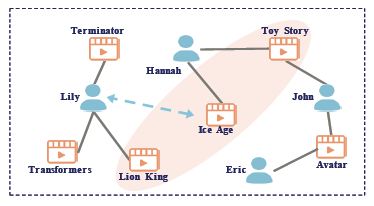
这是用户-电影二部图的示例，橙色阴影区域代表了一个基本的社区结构，这三部电影可能拥有相似的流派。蓝色虚线代表了Lily和《Ice Age》之间的长期依附关系。然而，很难从局部图结构中很好的学习这些全局性质。

为了识别二部图的全局性质，提出了新的基于互信息最大化的二部图嵌入算法BiGI。具体来说，BiGI首先引入一个全局表示，该表示由两个原型表示组成，每个原型表示通过聚合相应的同构节点来生成。然后，BiGI通过所提出的子图级别的注意力机制将采样边encode成局部表示。在此基础上，提出了一个新的局部-全局informax目标，以最大化局部和全局表示之间的互信息。这样，Informax目标可以通过最大化每个节点与其同类原型之间的MI来保持同类节点的社区结构，同时这也捕捉了异构节点的远程依赖关系。

---

RELARED WORK

2.1 Bipartite Graph Embedding

同构图和异构图嵌入表示通常用于二部图的建模；
用于同构图的方法：DeepWalk、LINE、Node2vec、VGAE；
用于异构图的方法：Metapath2vec，DMGI；
但这些不是为二部图量身定做的，因此二部图的结构特征很难被保留。IGE、PinSage、BiNE、FOBE是专门为二部图设计的。但它们主要集中在如何潜在空间中对局部图结构进行建模。

矩阵补全和协同过滤与二部图的建模密切相关。有很多DNNs的方法来解决推荐任务。例如：GC-MC、NGCF。但是他们仍然忽视了二部图的全局性质。

2.2 Mutual Information Maximization

最大化输入和潜在嵌入空间的MI为无监督学习提供了一个理想的范例。然而在高维连续设置中估计MI是比较困难的。MINE推到了MI的下界，并通过训练鉴别器来区分来自两个随机变量的联合分布或者其边缘的乘积的样本。DIM将结构信息引入到输入中，并采用不同的Infomax目标。

DGI是第一个将infomax目标应用于同质图的工作。基于DIM,InfoGraph试图通过最大化图级表示和子结构表示之间的MI来学习无监督的图表示。

DMGI将DGI扩展到异构图，将原始图形拆分成多个同构图形，并采用DGI中的Infomax目标对拆分图形进行建模。因此，DMGI仍然把重点放在学习同类节点的相关性上；

GMI提出了一种直接测量输入同质图和节点嵌入之间的MI的新方法。

与上述相比，文章中结合两种类型的结点信息来生成局部和全局表示，提出一种新的更适合于二部图的Infomax

BACKGROUND

G=(U,V,E)是一个二部图，U和V是两个不相交的节点集，\(E\subseteq U\times V\)表示边集，\(A \in \{0,1\}^{|U|\times |V|}\)是二进制邻接矩阵，其中每个元素\(A_{i,j}\)描述节点\(u_{i}\in U\)和\(v_j \in V\)有交互。给定一个二部图G=(U,V,E)和它的邻接矩阵，二部图嵌入表示的目标是映射G中的节点为d维的向量。\(u_i\)和\(v_j\)分别表示\(u_i\)和\(v_j\)的嵌入表示向量；

PROPOSED MODEL

BiGI首先设计一个基本的二部图编码器来生成初始节点表示。然后，将这些节点表示作为框架的输入，演示了如何构造全局表示、局部表示和局部-全局infomax目标；最后给出详细的模型分析；

4.1 Bipartite Graph Encoder

与同构图不同的是，二部图的每个节点都与相邻节点的类型不同。因此通过聚合一跳邻居的特征来直接更新节点嵌入式不适合的。为了解决这样的问题，文章的encode尝试从每一层的两跳邻居(two-hop neighbors)那里学习嵌入的每个节点。解释如下图：

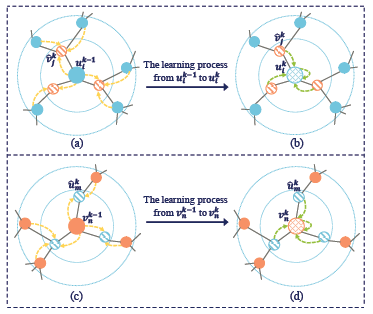
\(u_i^{k-1}\)和\(v_n^{k-1}\)的学习过程在\(k-th\)层有两个操作。以\(u_i^{k-1}\)为例，图中的a和b，首先通过一个具有非线性变幻的均值运算生成临时邻域表示\(\hat{v}_j^k\)，公式如下：

\[\hat{v}_j^k=\delta (\hat{W}_v^k \cdot MEAN(\{u_i^{k-1}:u_i \in N(v_j)\})) \]

\(\delta\)表示LeakyReLU激活函数，\(\hat{W}_v^k\)是一个权重矩阵，\(N_{(v_j)}\)是\(v_j\)的一跳邻域。与其他常用的图卷积不同的是，\(v_j^{k-1}\)并不纳入计算。因此，\(\hat{v}_j^k\)可以看成一种u-type(用户类型)节点的嵌入表示。之后使用同构图卷积来获得\(u_i^k\)，公式如下：

\[\bar{u}_i^k=\delta (\bar{W}_u^k \cdot MEAN(\{\hat{v}_j^k:v_j\in N(u_i)\})),\\ u_i^k=W_u^k\cdot[\bar{u}_i^k|u_i^{k-1}], \]

其中，\(\bar{W}_u^k\)和\(W_u^k\)是两个权重矩阵，\([\cdot | \cdot]\)是一种concatenation(连接操作)。
更新\(v_n^{k-1}\)也采用类似的步骤，图中的c和d说明了从\(v_n^{k-1}\)到\(v_n^k\)的学习过程，公式如下：

\[\hat{u}_m^k=\delta(\hat{W}_u^k \cdot MEAN(\{v_n^{k-1}:v_n\in N(u_m)\})) \]

\[\bar{v}_n^k=\delta(\bar{W}_v^k\cdot MEAN(\{\hat{u}_m^k:u_m\in N(v_n)\})) \]

\[v_n^k=W_v^k\cdot [\bar{va_n^k}|v_n^{k-1}] \]

其中\(\hat{W}_u^k,\bar{W}_v^k,W_v^k\)是权重矩阵，同时Dropout应用于编码器的每一层，以regularize模型参数。

4.2 Local-Global Infomax

此部分先介绍全局表示和局部表示的计算，然后介绍论文提出的局部-全局infomax目标来捕捉二部图的全局性质。

4.2.1 Global Representation全局表示

全局表示是二部图的整体表示，它通过一个简单合成函数(COM)生成的，这个简单合成函数结合了两个原型表示。具体地说，对于每种节点类型，引入一个原型表示来聚合所有同构节点信息。模型的insight和经典的few-show学习，它将生成每个类的原型表示。在文章中采用对所有同类节点信息进行平均的操作来获得相应的原型表示，公式如下：

\[p_u=MEAN(\{u_i:u_i\in U\}),\\ p_v=MEAN(\{v_i:v_i\in V\}),\\ g=COM(p_u,p_v)=[\sigma (p_u)|\sigma(p_v)], \]

其中\(u_i,v_i\)是encoder的输出，g是全局表示（由两个原型表示：\(p_u\)和\(p_v\)组成），\(\sigma()\)采用Sigmoid函数，以此来实现COM函数

4.2.2 Local Representation

局部表示的每个输入都是二部图的一条边，(u,v)。进一步，用一个h-hop封闭子图，来描述(u,v)的周围环境。下面给出h-hop封闭子图的具体定义：

• H-hop Enclosing Subgraph（H-hop封闭子图），给定一个二部图G=(U,V,E)，两个节点\(u\in U\)和\(v\in V\)，(u,v)的h-hop封闭子图\(G_{u,v}^h\)由G的两个节点集的并(\(G^h(u) \cup G^h(v)\))。其中

\[G^h(u)=\{v_i|dis(v_i,u)\leq h\}, \\ G^h(v)=\{u_i|dis(u_i,v)\leq h\} \]

dis是一个距离函数。由于二部图的特殊结果，h严格设定为奇数。

对于一个特定的边\((u,v)\in E\)和相应的h-hop封闭子图\(G_{(u,v)^h}\)(简单起见，省略了u和v的下标)，使用注意力机制来计算局部表示。给定节点u和\(v_j\in G^h(u)\)，关系权重\(\alpha_{u,i}\)表示如下：

\[\alpha_{u,i}=\frac{exp\{(W_a\cdot v_i)^\mathrm{T}\cdot (W_a^{'}\cdot u)\}}{\sum_{v_j\in G^h(u)}exp\{(W_a\cdot v_j)^\mathrm{T}\cdot (W_a^{'}\cdot u)\}}, \]

其中T表示转置，\(W_a\)和\(W_a^{'}\)是两个共享的可训练矩阵。类似，节点v和节点\(u_i\in G^h(v)\)被定义如下：

\[\alpha_{v,i}=\frac{exp\{(W_a^{'}\cdot u_i)^\mathrm{T}\cdot (W_a\cdot v)\}}{\sum_{u_j\in G^h(v)}exp\{(W_a^{'}\cdot u_j)^\mathrm{T}\cdot (W_a\cdot v)\}} \]

局部输入\(g_{(u,v)}^h\)的最终表示如下：

\[g_{(u,v)}^h=[\sigma(\sum_{v_i\in G^h(u)}\alpha_{u,i}v_i+u)|\sigma(\sum_{u_i\in G^h(v)}\alpha_{v,i}u_i+v)] \]

局部注意力表示还使用了相同的合成函数，结合了不同局部环境。这不仅突出了\((u,v)\)的中心作用，而且通过子图级别的注意力机制自适应地将不同的重要性分配给相邻节点。

4.2.3 Infomax Objective

在获得局部和全局表示后，local-global infomax objective被重新描述为噪声对比损失，其中正样本来自联合分布，负样本来自边的乘积。需要使用corruption函数C来生成负样本，并且BiGI使用破坏图结构A来定义C。切换参数\(S_{i,j}\)是拿来确定是否破坏邻接矩阵\(A_{i,j}\)，上述操作执行如下：

\[S_{i,j}=Bernoulli(\beta),\\ \tilde{G}=(U,V,\tilde{E})=C(G,\beta)=A\oplus S \]

其中\(\beta\)是损失率，\(\oplus\)表示异或运算，\(\tilde{G}\)是损坏图，\(\tilde{E}\)是相应的损坏边的集合，具体损失函数定义为：

\[L_m=-\frac{1}{|E|+|\tilde{E}|}(\sum_{i=1}^{|E|}\mathbb{E}_G[log \mathcal{D}(g_{(u,v)_i}^h,g)]+\sum_{i=1}^{|\tilde{E}|}\mathbb{E}_{\tilde{G}}[log(1-\mathcal{D}(g_{(u,v)_i}^h,g))]) \]

其中，\(\mathcal{D}\)通过双线性映射函数对局部-全局表示进行评分：

\[\mathcal{D}(g_{(u,v)_i}^h,g)=\sigma((g_{(u,v)_i}^h)^\mathrm{T}W_bg) \]

其中\(W_b\)是一个权重矩阵，二元交叉熵损失能够最大化\(g_{(u,v)_i}^h\)和\(g\)的MI。

4.3 Model Training

训练损失\(L\)包括两个部分：

\[L=\lambda L_M+(1-\lambda )L_r, \]

其中\(\lambda\)是谐波因数，\(L_r\)是一个margin-based排序损失，公式如下：

\[L_r=\sum_{(u,v)\in E}\sum_{(u^{'},v^{'})\in E_{(u,v)}^{'}}[\gamma +\phi([u^{'}|v^{'}])-\phi([u|v])]_+ \]

其中，\(\phi\)是排序函数，是一个两层MLP，\([x]_+\)表示x的正数部分，\(\gamma\)是边距，\(E_{(u,v)}^{'}\)是一个负样本节点对的集合，定义如下：

\[E_{(u,v)}^{'}=\{(u^{'},v)|u^{'}\in U\}\cup \{(u,v^{'})|v^{'}\in V\} \]

\(E_{(u,v)}^{'}\)由来自同一节点集合的随机节点替换头部或者尾部的交互来完成。BiGI是一个端到端的模型，使用了Adam来优化模型。整体架构如下图：

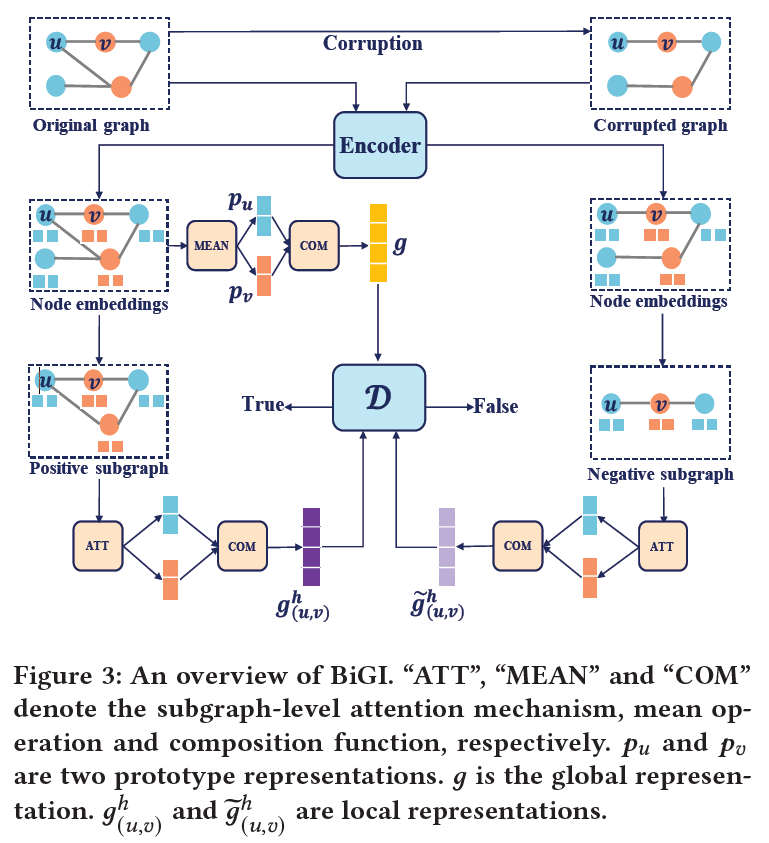
4.4 Model Analysis

4.4.1 Time Complexity

BiGI学习初始节点表示和计算总损耗，使用共享encoder来学习\(G\)和\(\tilde{G}\)的节点表示，来避免参数overhead。BiGI的计算复杂度近似为\(O(k(|E|+|\tilde{E}|)d^2)\)，其中k是层数，d是embedding size。

4.4.2 Relation with DGI

模型与DGI密切相关，因为它们都在图上使用局部-全局的infomax objective。然而，存在着一些设计差异：

1）BiGI专注于二部图的建模，将两种节点类型的信息集成到局部和全局表示中。相比之下，DGI是为同构节点嵌入而设计的；

2）DGI试图最大化节点和图级别表示之间的MI，而BiGI实际上最大化子图级别和图级别表示之间的MI。子图级别表示能够有效地保持采样边的丰富交互行为；

3）encoder的选择不同。鉴于二部图的结构特点，文章设计了一种新的basic encoder来学习初始节点表示。

EXPERIMENTS

5.1 Datasets

使用了四个基准数据集：DBLP,MovieLens-100K(ML-100K),MovieLens-10M(ML-10M),Wikipedia。其中DBLP,ML-100K和ML-10M用于top-K的推荐，Wikipedia用于连接预测。将用户-项目交互转换为隐式数据。统计数据如下表，可以看出ML-10M比其他数据集大很多，它是用于测试模型是否可以部署到大规模的二部图上。

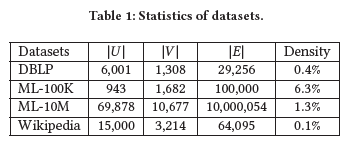
5.1.1 Data Preprocessing

• DBLP和ML-10M中，使用60%的数据用于训练，其余用于测试。
• 对于ML-100K，使用与IGMC相同的数据集划分
• 将Wikipedia数据划分为两个，Wiki(5:5)和Wiki(4:6)，即数据集的训练/测试比为5:5和4:6

5.2 Experimental Setting

5.2.1 Evaluation Metrics

在top-K推荐中，对于每个用户，首先过滤用户在训练过程中接触过的项目，然后，对剩余的项目进行排序，并使用一下评估指标对排名结果进行评估：F1, NDCG(Normalized Discounted Cumulative Gain), MAP(Mean Average Precision), MRR(Mean Reciprocal Gain)。

在连接预测(序列预测)，有两个常用的指标：AUC-ROC和AUC-PR

5.2.2 Compared Baselines

和以下几种类型的基准模型进行比较：

• Homogeneous graph embedding: DeepWalk, LINE,Node2vec,VAGE
• Heterogeneous graph embedding: Metapath2vec,DMGI
• Bipartite graph embedding: PinSage, BiNE
• Matrix completion: GC-MC, IGMC
• Collaborative filtering: NeuMF, NGCF

5.2.3 Implementation Details

为了比较的公平，节点的编信息没有被使用。embedding size固定为128，learning rate是0.001，迭代轮数为100到收敛。在有效性和效率之间取得平衡，按照IGMC的建议，使用1-hop封闭子图。encoder的深度k为2，模型中的\(\gamma\)为0.3，图的损坏比率\(\beta\)在\(\{1e-6,1e-5,1e-4,1e-3,1e-2,1e-1\}\)中进行选取，谐波因数\(\lambda\)从0.1至0.9进行选取，步长为0.2

5.3 Top-K Recommendation

下表展示了在DBLP,ML-100K,ML-10M上，比较的方法的性能，最好的结果用*标记，次优的结果加上了下划线；

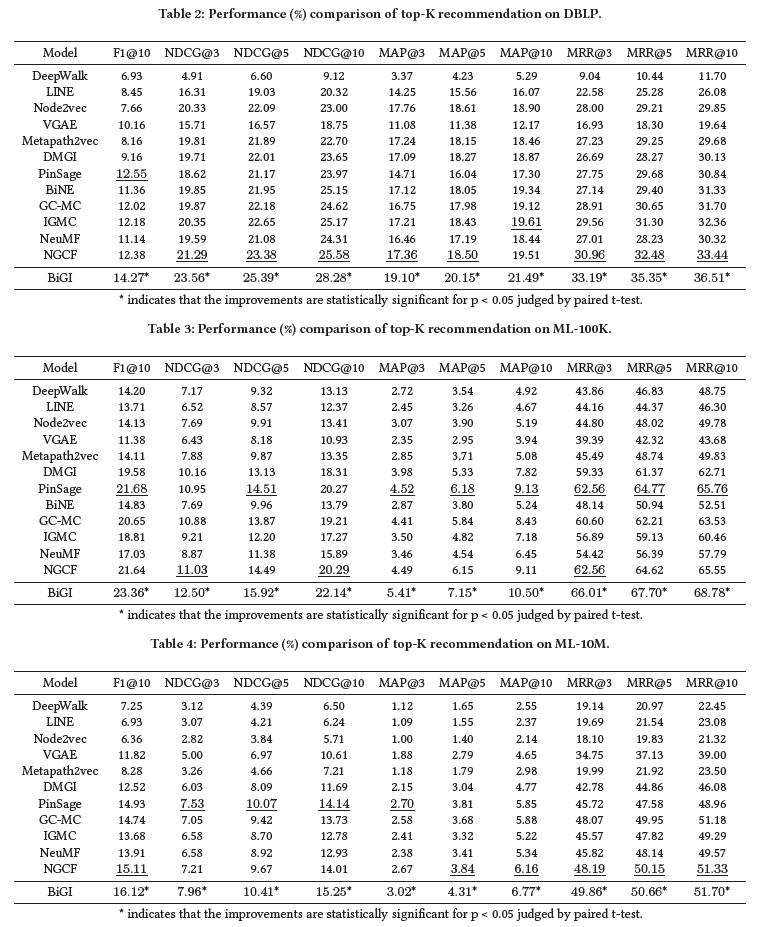
可以观察到：
1）对于所有metric，BiGI取得了最好的性能，证明了二部图全局性质的高效；
2）二部图的结构特征建模是很重要的，同构和异构图忽略了这些特性，以至于效果不如BiGI和其他二部图嵌入模型；
3）DMGI也最大化了局部-全局表示之间的MI，但是性能较差，因此BiGI的核心工作：设计一个合适的infomax objective；

5.4 Link Prediction

对于序列预测，在给定节点对\((u_i,v_j)\)，将对应的嵌入表示\(u_i\)和\(v_j\)输入Logistics回归分类器，这个分类器是基于二部图的交互边来训练的。下表展示了结果，结果表示BiGI取得了最好的结果。证明了二部图的全局性质有利于节点表示的学习，特别是，捕获异构节点的远程依赖关系，这有助于下游任务；

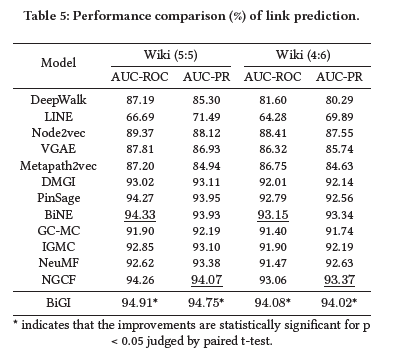
5.5 Discussions of Model Variants

文章研究了不同局部表示的效果以及所提出的Infomax objective的可扩展性。下表提供了这些变体模型的结果和所提出的encoder的消融实验研究

• BiGI(node)使用每个节点的嵌入表示作为局部表示；
• BiGI(pair)简单地将节点对(u,v)的表示进行连接作为局部表示；
• BiGI(w/o att)通过均值运算来计算子图的表示，而不是使用注意力机制；
• BiGI(VGAE),BiGI(NGCF),BiGI(PinSage)分别采用VGAE、NGCF和PinSage作为encoder。

这些变体模型都保持着相同的Infomax objective

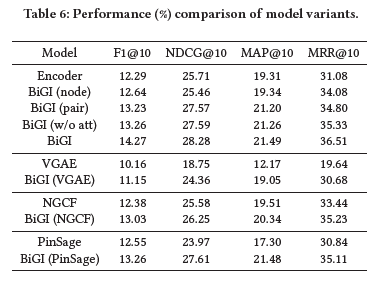
从表中可以得出以下结论：
1）所提出的encoder取得了很不错的效果，同时BiGI的改进效果也是很显著的；
2）通过比较不同的局部表示，发现合适的局部表示是BiGI的关键，子图级别的注意力机制是一个很好的选择；
3）与VGAE、NGCF和PinSage相比，BiGI(VGAE),BiGI (NGCF)和BiGI(PinSage)的改进效果很不错。这表明，所提出的Infomax objective可以无缝地集成到其他编码器中，一次捕获二部图的全局性质；

5.6 Parameter Sensitivity

损失率\(\beta\)和谐波因数\(\lambda\)是两个超参数。如下图所示，当\(\beta =1e-5\),\(\lambda =0.3\)时，BiGI达到了最佳结果。因此较小的\(\beta\)和\(\lambda\)是合理的。同时模型具有较好的鲁棒性，即使\(\beta\)和\(\lambda\)最差的效果也比其他基准模型更好；

5.7 Analysis of the Global Properties

此部分研究BiGI相比其它模型能够更好地捕获二部图的全局表示，进行了两个实验:

• 第一个实验：对ML-100K上的用户和项目进行聚类分析，首先保存用户和项目的所有标示，然后通过KMeans算法进行聚类，结果如下图所示，与其他图嵌入表示相比，BiGI在不用聚类数的情况下都取得了最好结果，这表明，BiGI能够更好地捕获用户和项目的社区结构
  
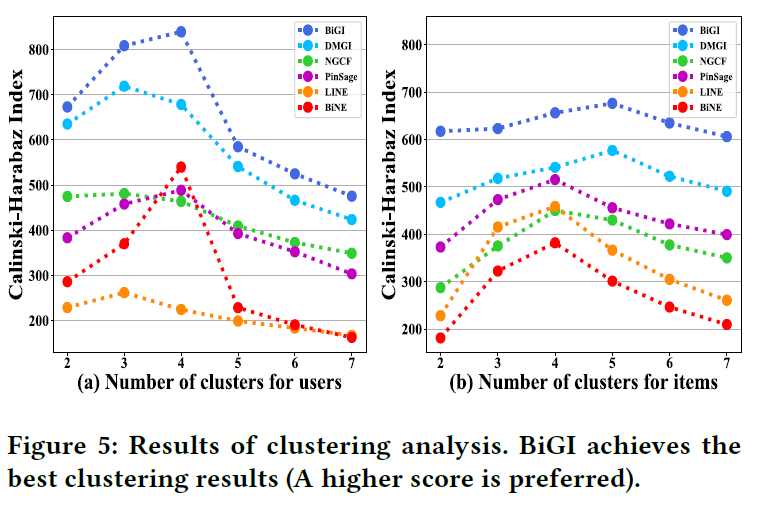
• 第二个实验：建模BiGI能否学习到异构节点的远程依赖关系。从DBLP的测试数据集中随机抽取15个节点对\(\{(u_i,v_j)\}\)，用BiGI和其他几种基准方法进行预测。根据\(u_i\)和\(v_j\)之间的距离，这些节点对可以分为三组。这里的距离可以分为3、5、7。实验结果如图，可以看出：
  1）当目标节点对的距离相对较短时候，例如3，所有的基准模型和BiGI都能都学习到节点对之间的潜在交互；
  2）随着距离增加，\(u_i\)和\(v_j\)之间的关系逐渐减弱。与soat baselines相比，BiGI仍然保持优异的效果。这证明了BiGI能够学习到异构节点\(u_i\)和\(v_j\)的远程依赖关系；

CONCLUSION

文章提出的二部图嵌入算法BiGI能够更好地学习初始节点表示，然后通过聚合不同的同构节点信息生成两个原型表示，并以此构造全局表示。

将子图级别的注意力机制融入到局部表示中。

通过最大化局部表示和全局表示之间的MI，BiGI能够有效地识别二部图的全局属性。