机器学习中的数学系列-信息论

1,信息

\( i(x)=-log(p(x)) \)

事件x不确定性的度量，不确定性越大，信息量越大。

从信息编码角度，这是编码这一信息所需要的最小比特数(log以2为底，以e为底的叫做奈特)。

2,熵

\( H(X) = \sum_x{-p(x)log(p(x))} \)

随机变量X不确定的度量，信息的期望，不确定性越大，熵越大。

从信息编码角度讲，熵是对信息进行编码所需要的平均比特长度的最低值。

 

3，联合熵

\( H(X,Y) = \sum_{x,y}{-p(x,y)logp(x,y)}\) 

4，条件熵

\( H(X|Y) = H(X,Y) - H(Y)  \)

\( = -\sum_{x,y}p(x,y)logp(x,y)+\sum_yp(y)logp(y) \)

\( = -\sum_{x,y}p(x,y)logp(x,y)+\sum_y\sum_xp(x,y)logp(y) \)  #边缘概率

\( = -\sum_{x,y}p(x,y)log\frac{p(x,y)}{p(y)} \)

\( = -\sum_{x,y}{p(x,y)logp(x|y)}\)

熵，联合熵，条件熵的关系

 

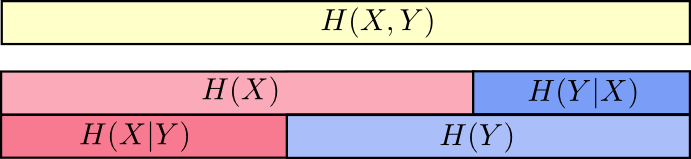
5，互信息

描述事件x发生后，对事件y不确定性的消除

i(y,x) = i(y)-i(y|x) = log(p(y|x)/p(y)) = log(后验概率/先验概率)

对称性:i(y,x)=i(x,y)

6，平均互信息

\( I(X;Y)= \sum_{x,y}{p(x,y)i(x,y)}= \sum_{x,y}{p(x,y)log\frac{p(y|x)}{p(y)}}= \sum_{x,y}{p(x,y)log\frac{p(x,y)}{p(x)p(y)}} \)

= H(X)-H(X|Y)  ----信息增益

= H(Y)-H(Y|X)

=H(X)+H(Y)-H(X,Y)

=H(X,Y)-H(X|Y)-H(Y|X)

=D(p(x,y)||p(x)p(y))

在有些文章里，会把平均互信息叫做互信息。

熵、联合熵、交叉熵、互信息的关系

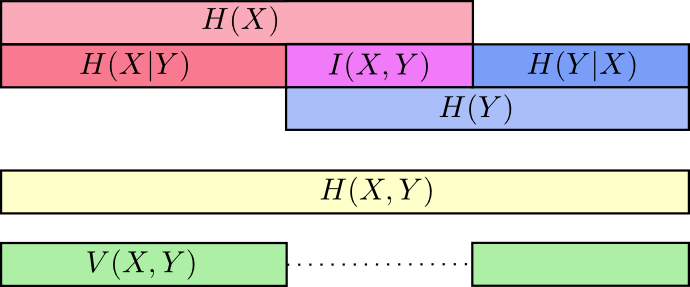
V(X,Y)，variation of information is the information which isn’t shared between the variables.

V(X,Y)=H(X,Y)−I(X,Y)

 

7，交叉熵

衡量两个分布的差异性

\(H(p|q)=-\sum_x{p(x)logq(x)}\)

可以认为p为真实分布，q为近似分布。

8，相对熵(KL散度)

Kullback-Leible散度,也是用于衡量两个分布的差异性

\( KL(p||q) = \sum_x{p(x)log\frac{p(x)}{q(x)}} \)

很容易推导得到KL(p||q)=H(p|q)-H(p)

 H(p)用来表示编码的期望长度，H(p|q)表示用近似分布编码的期望长度。我们将由q得到的平均编码长度比由p得到的平均编码长度多出的bit数称为“相对熵”，也就是KL散度。

比如TD-IDF算法就可以理解为相对熵的应用：词频在整个语料库的分布与词频在具体文档中分布之间的差异性。

交叉熵和KL的关系

 

总结：

 参考1：http://colah.github.io/posts/2015-09-Visual-Information/

 参考2：https://www.zhihu.com/question/41252833