关于二分图的一些概念

这将是很漫长的一条路，这条路从二分图开始，它的终点将是二次匹配问题(QAP)。

最近在研究分配问题，看到了二分图，在网上搜索了很多关于二分图的资料，但是我发现中文资料中对二分图相关概念的定义并不是很准确。现在我把我需要了解的内容整理如下。

（1）二分图的定义

In the mathematical field of graph theory, a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint sets and such that every edge connects a vertex in to one in ; that is, and are each independent sets. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.[1]

One often writes 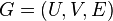to denote a bipartite graph whose partition has the parts and .[1]

（2）匹配

匹配这个概念并不是二分图独有的，它是图论里面的一个概念。

Given a graph G = (V,E), a matching M in G is a set of pairwise non-adjacent edges; that is, no two edges share a common vertex.[2]

从这个定义可以看出一个match是图G边的子集。

A vertex is matched (or saturated) if it is an endpoint of one of the edges in the matching. Otherwise the vertex is unmatched.[2]

(3)Maximal Matching

A matching M is said to be maximal if M is not properly contained in any other matching. [4]

这个就是说当我们不能再往M里面添加任何一条边的时候，再添加一条就不是一个匹配的时候，Ｍ就是maximal的了。

找一个maximal Matching还是很容易的。

(4)Maximum Matching

A maximum matching is a matching that contains the largest possible number of edges. There may be many maximum matchings.[2]

(5)Augmenting path （增广路径）[4]

有一条定理：A matching M is maximum iff it has no augmenting path.这个是个充要条件。

注意：匹配，maximal matching,maxsimun matching, augmenting path并不是二分图才有的概念，是所有图都有的概念。

(4)最大匹配：包含边数最多的匹配。 匈牙利算法 [3]

(5)完美匹配：所有点都在匹配边上的匹配。[3]

(6)完备匹配：在二分图中，X中的所有点都有对应的匹配或者是Y集中所有的点都有对应的匹配。[3]

(7)最佳匹配：如果G为加权二分图,则权值和最大的完备匹配称为最佳匹配。KM算法 [3]

参考：

[1] http://en.wikipedia.org/wiki/Matching_%28graph_theory%29#cite_note-Wes01-1

[2]http://en.wikipedia.org/wiki/Maximum_weight_matching

[3]http://www.cnblogs.com/one--world--one--dream/archive/2011/08/15/2139454.html

[4]http://www.cs.dartmouth.edu/~ac/Teach/CS105-Winter05/Notes/kavathekar-scribe.pdf