总结

总结

day1

T1 树上油量 to do

树剖线段树+分类讨论贪心+【矩阵乘法+向量乘矩阵】

贪心：

• 在花费次数最小的前提下使出去时的油量最多。
• 有时花更多次数使出去时油量更多更优。只需多跳一次就可使出去时油量最大。

向量乘矩阵：降低询问复杂度。

T2 友好城市 to do

回滚莫队+【强联通（kosaraju）+bitset】

多组 $[l,r]$ $\Rightarrow$ 莫队。

计算可互相到达的城市对数 $\Rightarrow$ 强联通。

稠密图 $n^2$ 条边，Tarjan 多次询问计算复杂度 $O(qn^2)$，不行。

koaraju：

• dfs1：遍历每个点，回溯时塞入队尾，求得后序遍历。
• dfs2：逆遍历“后序遍历”，对于没访问过的点 $u$，在反图上遍历，能访问到的所有点都跟 $u$ 在一个 scc 中。

dfs 中对于每个点不需遍历每条出边，只需找它的后继中第一个没遍历过的点，可用 bitset 的 &,^ 和 _Find_first() 优化到 $O(q\frac{n^2}{w})$。

for(now=mp[x]^(mp[x]&vis);now.any();now=mp[x]^(mp[x]&vis))

$now$ 为二进制01序列，$mp=1$ 且 $vis=0$ 的位为1，其余位为0。

bitset 函数：

• reset() 清零。

• set(x) 或 s[x]=1 x 位设为1。

• any() 存在一个1。

• _Find_first() 找第一个1的位置。

inline void dfs(int x)
{
    bs now;vis[x]=1;
    for(now=mp[x]^(mp[x]&vis);now.any();now=mp[x]^(mp[x]&vis))
        dfs(now._Find_first());
    out[++ind]=x;
}
inline int dfsrev(int x)
{
    int res=1;bs now;vis[x]=1;
    for(now=rmp[x]^(rmp[x]&vis);now.any();now=rmp[x]^(rmp[x]&vis))//反图
        res+=dfsrev(now._Find_first());
    return res;//连通块大小
}
inline int kosaraju()
{
    vis.reset();ind=0;
    for(int i=1;i<=n;++i) if(!vis[i]) dfs(i);
    vis.reset();int res=0;
    for(int i=n,x;i;--i) if(!vis[out[i]])
        x=dfsrev(out[i]),res+=x*(x-1)/2;
    return res;
}

回滚莫队：

• 当插入/删除操作一方好实现、另一方困难时，考虑用回滚莫队

• for：左端点所在的块

  • 左右端点同块的直接暴力，跳过。

  • 右端点的信息直接继承入累计影响，向指定方向推进

  • 左端点每次从块尾部向前推，用于更新当前的答案，但是不计入累计影响

  • 更新当前询问的答案

  • 回滚左端点，去掉对数组的影响

  • 回到只有块右侧有贡献的状态

• 注意左右端点初始值的设置：与待会左右端点的推进方向有关，保证不多删

T3 竞赛图路径

竞赛图+容斥

竞赛图

竞赛图就是给一个完全图的所有边指定一个方向的图。 （定了向的完全图）

“竞赛”图：一条边代表两个人之间比赛的输赢情况。

性质：

• 竞赛图必定有哈密顿路径（经过每个点恰一次的路径）。

• 如果竞赛图强连通，则它必有哈密顿回路。

• 如果竞赛图有一个大小为 $k(k>3)$ 的环，那么一定有大小为 $k−1$ 的环。

• 将竞赛图缩点后，将会得到一个 DAG，并且这个 DAG 有一条哈密顿路径（也可以理解为这是一条链，并且前面的点连向后面所有节点）。

• 证明：https://www.cnblogs.com/acha/p/9042984.html

结论：点 1 能到达的最长简单路径长度即为点 1 能访问到的所有点个数。

证明：竞赛图缩点后成链状，每个 scc 都是竞赛图，因此每个 scc 中都有哈密顿回路。可先沿着哈密顿回路遍历 1 所在 scc 的所有点，再沿着链依次遍历所有下游的 scc 里的所有点。

$x$ 个有标号点构成的竞赛图数：任挑两点连边，枚举每条边的方向。
$$
f(x)=2^{\begin{pmatrix} x \2 \end{pmatrix} }
$$
$x$ 个有标号点构成的强连通竞赛图数：

容斥。若该竞赛图不是强连通，枚举链头所在的 scc 大小，由 $g( 小)$ 推到 $g(大 )$。
$$
g(x)=f(x)-\sum_{y=1}^{x-1}g(y)f(x-y)
$$
计算答案：

枚举 1 所在的强连通大小 $x$，下游（能到达）点数 $y$，则上游（不能到达）点有 $n-x-y$ 个。
$$
ans_{x+y}+=\begin{pmatrix}n-1\x-1 \end{pmatrix}\begin{pmatrix}n-x\y \end{pmatrix}g(x)f(y)f(n-x-y)
$$

T4 异或区间 to do

暴力根号分治+二维数点（分块法）+差分

• 每次操作：$[L,R]$ 内所有被“关心”的 $[l,r]$ 都区间加上 $w$。

• 方法一可用二维数点，统计每个 $[l,r]$ 会接收到的 $\sum w$。$[L,R]$ 作为影响的发射器，$[l,r]$ 作为影响的接收器，

  • 排序满足一维偏序，树状数组/分块满足另一维。
  • 按端点排序，扫描线，扫到的发射器计入影响（修改），接收器计算收到的影响（查询）（树状数组或分块）。
  • $[l,r]$ 有 $O(n^2)$ 个，$[L,R]$ 有 $O(m)$ 个，若用 BIT，则修改 $O(m\log n)$，查询 $O(n^2\log n)$（TLE）。
  • 用分块，单次 $O(\sqrt n)$ 修改，$O(1)$ 查询，总共 $O(m\sqrt n+n^2)$，可行。

• 方法二：差分。差分数组 $c_i$。

  • 记前缀异或和为 $s_i$，则 $s_{l-1} \bigoplus s_r=k$ 为 $[l,r]$ 被关心的充要条件。

  • 对于 $[L,R]$ 内的每个 $l$ 对应的 $l-1$ 找有多少个匹配的 $r$，$c_l$ 就能加上几个 $w$。设 $s_{l-1}=x$，则 $s_r=k \bigoplus x$。枚举 $x$。

  • $$
    \forall l-1 \in [L-1,R-1],s_{l-1}=x,\
    c_l+=w\sum_{r=l}^R[c_r=k \bigoplus x]
    $$

  • 对于 $[L,R]$ 内的每个 $r$ 找有多少个匹配的 $l-1$，$c_{r+1}$ 就要减去几个 $w$。

  • $$
    \forall r \in [L,R],s_r=k\bigoplus x,\
    c_{r+1}-=w \sum_{l-1=L-1}^{r-1}[c_{l-1}=x]
    $$

  • 对每个 $x$ 预处理前缀 $s_j=x,j\leq i$ 的个数 $pre_i$，后缀 $s_j=k\bigoplus x$ 的个数 $suf_i$。

  • $$
    \forall l-1 \in [L-1,R-1],s_{l-1}=x,
    c_l+=w(suf_l-suf_{R+1})\
    \forall r \in [L,R],s_r=k\bigoplus x,
    c_{r+1}-=w(pre_{r-1}-pre_{L-2})
    $$

  • 每次操作 $[L,R]$ 在差分数组上打标记 $(L,+w),(R+1,-w)$，最后做两次前缀和，第一次算出 $c$ 数组，第二次算出 c 的前缀和即答案。

  • 设 $x$ 值域为 $a$，$O(|a|(n+m))$。

• 根号分治：

  • 对于全局出现次数 $\leq S$ 的 $x$ 采用方法一，其余采用方法二。
  • 取 $S=\sqrt n$，$O(\sqrt n (n+m))$。方法二常数较大，$S$ 可适量开大。
  • 复杂度分析：
  • $cnt>\sqrt n$ 的 $x$ 小于 $\sqrt n$ 个，$|a|<\sqrt n$。
  • $cnt<\sqrt n$ 的 $x$：瓶颈在于 $[l,r]$ 个数。
  • $s_r\bigoplus s_{l-1}=k$，对于特定的 $r$，$s_r=k\bigoplus x,s_{l-1}=x$，对应的 $l$ 个数即为 $s_{l-1}=x$ 个数，即 $cnt_x$。
  • $n$ 个 $r$，每个对应 $<\sqrt n$ 个 $l$，$[l,r]$ 个数 $O(n\sqrt n)$。
  • 总复杂度 $O(m\sqrt n+n\sqrt n)=O((n+m)\sqrt n)$。

day2 to do

To learn：

• 整除分块：

https://www.cnblogs.com/peng-ym/p/8661118.html

• $O(\sqrt n)$ 计算 $\sum_{i=1}^{n}\lfloor \frac{n}{i} \rfloor $
• $i=l,l+1,l+2,...,r$ 时 $\lfloor \frac{n}{i} \rfloor$ 值相同，$r=n/(n/l)$，可一起计入答案。

for(int l=1,r;l<=n;l=r+1)
{
	r=n/(n/l);
	ans+=(r-l+1)*(n/l);
}

• 复杂度分析：$\lfloor \frac{n}{i} \rfloor$ 的每个不同值会花费 $O(1)$ 的时间，因此复杂度为$\lfloor \frac{n}{i} \rfloor$ 的不同值个数。

• 莫比乌斯反演：

https://www.cnblogs.com/peng-ym/p/8647856.html

• 杜教筛：

https://www.cnblogs.com/peng-ym/p/9446555.html

day3

T1 选数博弈

• 若存在下标 $i$ 使得 $a_i=$当前 $a$ 最大且 $b_i=$ $b$ 最大，则先手选择 $i$ 必胜。
• 否则，可删去所有 $a_i=$当前 $a$ 最大或 $b_i=$ $b$ 最大的下标 $i$，因为先手一定不能选它。
  • 一旦先手选当前 $a_m$，则后手可选到 $a_i<a_m,b_i=b_m$ 的 $i$ 使先手没得选。
• 若最后都删光了，说明先手第一步没有使全局必胜的选择。
• 排名用 set 动态维护。删去一个下标 $i$ 要同时禁用 $a_i,b_i$。
• $O(n\log n)$

T2 AW距离

• 在一条边上移动完后不会再有涉及到该边的修改，可相当于断掉这条边。

• 因此对于每条边考虑对答案距离的贡献：

• 设该边在一种定向方案中被计入答案 $ct$ 次，对总答案贡献为：$2^{n-1}E(ct)$。

• 按输入顺序考虑边，对于边 $(u,v)$：

• 设整棵树在 $u$ 一侧的 $\sum a=c_u$，在 $v$ 一侧的为 $c_v$。$p_{u,i}$ 为 $u$ 结点当前有 $i$ 个 AW 的代价。

• 定向为 $u->v$ 时期望为：
  $$
  \frac 1 2 \sum_x p_{u,x}(c_u-x)(c_v+x)
  $$

  • 一旦 $u->v$ 移动完，断边 $(u,v)$，$u,v$ 两侧的点不管后续如何移动都不会跨过边 $(u,v)$，因此两两相距一定包含边 $(u,v)$。
  • $v->u$ 同理。

• 化简得
  $$
  \frac 1 2 (c_uc_v\sum_x p_{u,x}+(c_u-c_v)\sum_xp_{u,x}x-\sum_xp_{u,x}x^2)
  $$

• $\sum_x p_{u,x}=1$。设 $f_u=\sum_x p_{u,x}x,g_u=\sum_x p_{u,x}x^2$。$f_i$ 即 $i$ 结点当前期望 AW 个数。

• 初始 $f_i=a_i,g_i=a_i^2$。

• 对 $(u,v)$ 定向并移动 AW 后，
  $$
  f'_u=f'v=\frac{f_u+f_v} 2\
  g'u=g'v=\frac 1 2\sum_x\sum_ypp(x+y)^2=\frac 1 2(g_u+g_v)+f_uf_v
  $$

• 综上先预处理子树和 $\sum_a$，在对每条边计算贡献，更新 $f,g$。

• $O(n)$。

T3 停车场 to do

• 并联只有两条支路，可建成二叉树的结构。
• 对于每个子树内，车能否出去只跟当前子树的源和汇是否与出口连通有关。
• 记二位二进制数表连通情况，DP。

T4 找极小环 to do

邻域 $N(x)$：与 $x$ 直接相邻的所有点。


day 4

T1 优美子序列

枚举分界点 $p$，计算 $s[1,p]$ 与 $s[p+1,n]$ 的 LCS。

最长公共子序列LCS：

• 子串：连续。
• 子序列：不连续。

$O(n^2)$ DP：

• 设 $f(i,j)$：$A[1,i]$ 与 $B[1,j]$ 的 LCS 长度。

• $$
  f_{i,j} =
  \begin{cases}
  f_{i-1, j-1} + 1 & (A_i = B_j) \
  \max(f_{i, j-1}, f_{i-1, j}) & (A_i \ne B_j)
  \end{cases}
  $$

$O(\frac {n^2} w)$ 位运算优化：
$$
f(i-1,j-1) \leq f(i,j-1),f(i-1,j) \leq f(i,j)\
|f(i,j)-f(i-1,j-1)|\leq 1
$$
因此每行 $f$ 的差分数组由 $0,1$ 构成。

定义：

• $Row_i$ 为第 $i$ 行 $f$ 的差分数组的 01 序列。
• $c- string$ 为 A 每一位是否为 $c$。

$$
X=Row_i | B_istring\
Row_i = ((X-((Row_{i-1}\ \texttt{<<}\ 1) + 1))\ \texttt{xor}\ X)\ \texttt{and}\ X
$$

$Row_{|B|}$ 中 1 的个数即为答案。__builtin_popcountll。

手写 bitset 支持与、或、异或、位移、减法即可。本质是压位高精。

c=1llu;
for(int i=0;i<blo;i++){
    x=f[i];y=x|mp[b][i];		
    x+=x+c+(~y&((1llu<<B)-1));  
    f[i]=x&y;c=x>>B;		    
}

#include<bits/stdc++.h>
#define ull unsigned long long
using namespace std;
const int S=10,B=63,N=7e4/B+100;
int n,m,a,b,blo,ans;
ull f[N],mp[S][N],x,y,c;
int main(){
    scanf("%d %d",&n,&m);
    for(int i=0;i<n;i++){
        scanf("%d",&a);
        mp[a][i/B]|=1llu<<(i%B);
    }
    blo=(n-1)/B+1;

    while(m--){
        scanf("%d",&b);
        c=1llu;
        for(int i=0;i<blo;i++){
            x=f[i];y=x|mp[b][i];		//
            x+=x+c+(~y&((1llu<<B)-1));  //
            f[i]=x&y;c=x>>B;		    //
        }
    }
    for(int i=0;i<blo;i++) ans+=__builtin_popcountll(f[i]);
    cout<<ans<<"\n";
    return 0;
}

T2 正三角形 to do

分三类：正三角形、倒三角形、正六边形中的两个内三角形。

对于每个点分别计数，形如 $\min (i-y,r-i)$。$O(qr^2)$。

拆开 $\min$，对每行 $i-y<r-i$ 的 $(i,y)$ 一起计数。$O(qr)$。

把增减一行的贡献表达为 $O(1)$ 可计算的表达式，莫队。$O(\sqrt q r)$。

写出三角形个数关于 $l,r$ 的多项式，每次 $O(1)$ 代入 $l,r$ 求值。$O(q)$。

T3 博弈移棋 to do

T4 中位数序列 to do

中位数 trick：二分中位数大小，看有多少个数大于它来调整值。

To be continued...

day 5

T1 斐波那契

大眼观察+矩阵快速幂

若奇数项、偶数项的转移矩阵不同，分别设为 $T1,T2$。
$$
F_n=F_1(T2T1)^{\lfloor \frac {n-1} 2 \rfloor}\
F_n=F_n*T2~~if(n \mod 2=0)
$$
T2 不降序列

费用流

$a_i>0$ 则 lk(src,i,a[i],0)，否则 lk(i,des,-a[i],0)。

要求连向汇点的边全部满流，则只需正常地跑最小费用最大流，最后判断 $mf==\sum_{a_i<0}-a_i$。

T3 炮弹轰炸 to do

线段树历史最大值：

https://www.cnblogs.com/LightningUZ/p/14726808.html

板子：洛谷4314 CPU监控

支持区间加、赋值，查询区间当前最大值和历史最大值。

维护值：

• ad 当前加法懒标记。 had 当前操作序列中加法懒标记前缀和最大值。
• cv 当前赋值懒标记。hcv 当前操作序列中赋值懒标记前缀最大值。
• hfad 父亲下放的操作序列中加法懒标记前缀和最大值。
• hfcv 父亲下放的操作序列中赋值懒标记前缀最大值。
• mx 区间当前最大值。hmx 区间历史最大值。

pushdown：相当于把父亲的操作序列接在儿子操作序列后面。

1.只含加法时：

void addone(int k,int fad,int hfad){
	had[k]=max(had[k],ad[k]+hfad);//历史值要先更新
	hmx[k]=max(hmx[k],mx[k]+hfad);//因为要用到 ad,mx
	ad[k]+=fad;mx[k]+=fad;
}

任意时刻的当前值为操作序列执行一段前缀操作后的结果。因此，若要加上父亲操作序列内的最大加法前缀和，必须先选择自己操作序列中的所有操作。

2.包含加法和赋值（覆盖）时：

第一次区间赋值之后的所有加法都可看作赋值。=x,+c -> =x,=x+c 。

因此操作序列可化简为 +,+,+,...,=,=,=,...。

讨论已有赋值时的情况：

• 先接父亲的加法操作：

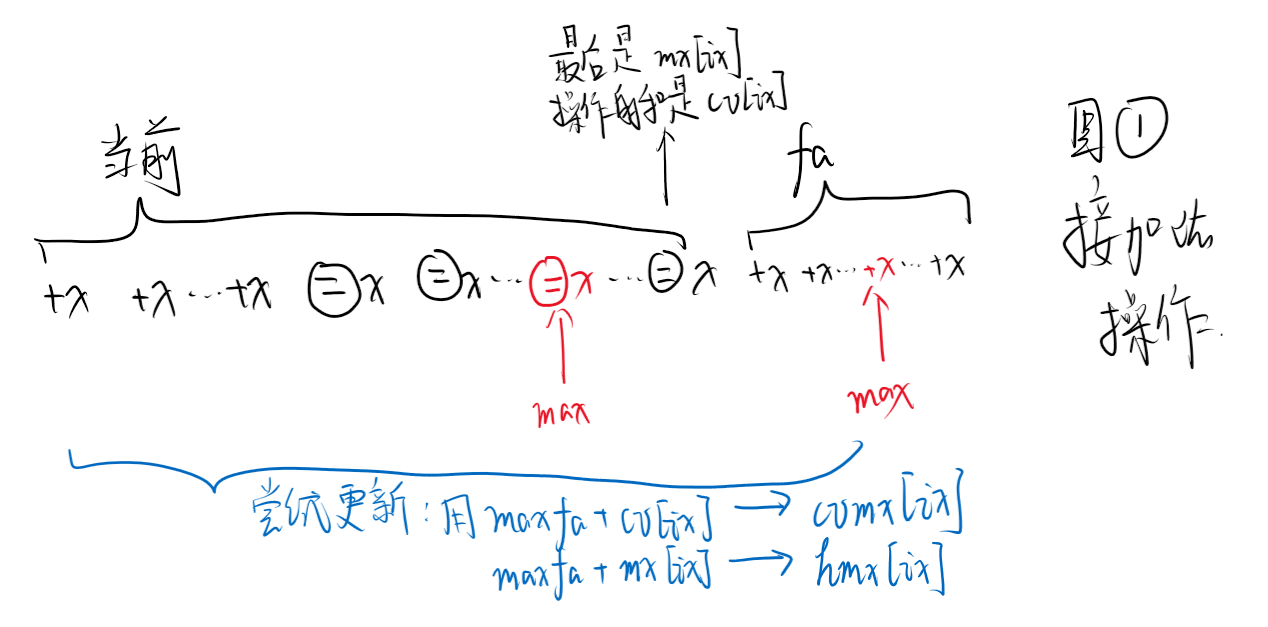
-> 表 max 更新
cv[k]+hfad -> hcv[k]
mx[k]+hfad -> hmx[k]
mx[k]+=fad;cv[k]+=fad;

• 再接父亲的赋值操作：

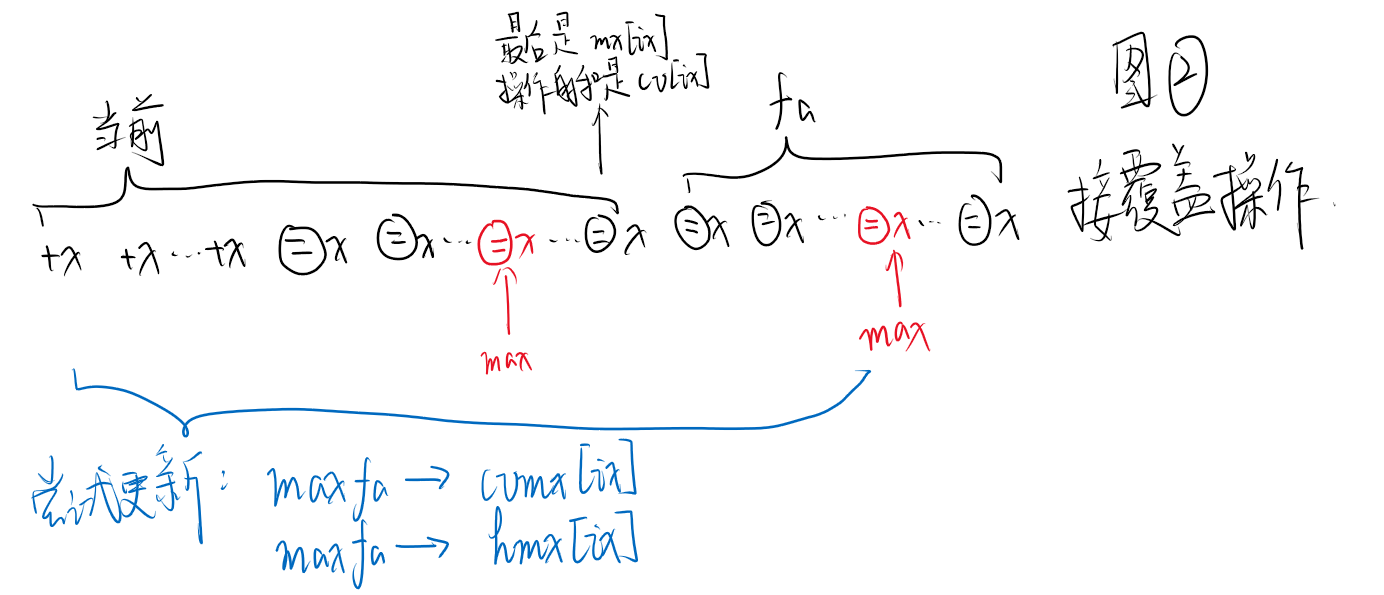
hfcv -> hcv[k]
hfcv -> hmx[k]
mx[k]=cv[k]=fcv;

具体实现时要标记当前区间是否被整体赋值过。若还未则自己序列只有加法。

**3. 支持若干区间 (+a,对b取max) 的操作 **

http://uoj.ac/problem/164

(+a,对b取max) 这个东西可以合并，$(a,b)+(c,d)=(a+c,max(b+c,d))$。

空操作为 $(0,-INF)$。

证明：

考虑一开始有一个 x

做完第一个变成 max(x+a,b)

做完第二个变成 max(max(x+a,b)+c,d)

=max(max(x+a+c,b+c),d)（把 c 放进 max 里）

=max(x+a+c,max(b+c,d))

求历史最大值，即求进行前缀操作后的最大值。

设两时刻 $i,j$，$(a.ad,a.jp),(b.ad,b.jp)$ 分别为 $[1,i],[1,j]$ 操作的合并和。

对于$(a.ad ,a.jp)$，$a.jp>x+a.ad,x<a.jp-a.ad$，所以 $x$ 较小时 $max=a.jp$，较大时 $max=x+a.ad$。

因此时刻 $i,j$ 的最大值为图像 y 靠上的部分，相当于只执行$(max(a.ad,b.ad),max(a.jp,b.jp))$。

op operator*(op x,op y) {return (op){max(x.a,y.a),max(x.b,y.b)};}
// 用乘法表示历史最大值的更新

day 6

T1 波西米亚狂想曲

差分+扫描线+数列剖分+转化题目操作

• 对 $[l,r]$ 的树进行操作，可转换为差分 upd(l,-1);upd(r+1,+1)。这样扫描线从第一棵树扫到第 $m$ 棵，只需继承上一棵树的情况，再添加上我自己这棵树的修改。那么修改需要方便撤销。
• 考虑每条边的权值：对于点 p 连向父亲的边，$sz[p]*(n-sz[p])$。
• 一次收缩操作 l,r,u,v 即相当于在 $(u,v)$ 的路径上保留标记 -1。撤销即标记 +1。当 $-1$ 且标记次数=0 时要减去这条边的权值， +1 且标记次数=1 时要加上。相当于路径覆盖。
• 为什么只用减去边的权值？收缩若干条边，每条边权值为上侧音符数 $*$ 下侧音符数，即权值。从下往上收缩，不论下侧的音符怎么移动都在下侧。
• 为什么收缩音符 $u,v$ 所在的点的路径可以直接收缩点 u,v 所在的路径？假设音符 u,x 在上次收缩移动到了 $LCA (u,x)$ 点，则题意要求为 LCA 与 v 的简单路径，我们实现的是覆盖 u 与 v 的路径。
  • 若 v 在 LCA 子树外：会多覆盖 (u,LCA) 这段已被收缩的路径。这段路径也打上标记，这样撤销这次操作时 (u,LCA) 的标记还在。但不会涉及对答案的更改（见第3点）。
  • v 在 u 子树内：我们覆盖的即为当前（已经收缩若干边后）要求的路径。
  • 总之要么刚好覆盖，要么比题目要求多覆盖一段已被收缩的边，而在这些边上面打标记时合理的。

day15

T3 达尔文芯片问题

四边形不等式优化区间DP：

https://oi-wiki.org/dp/opt/quadrangle/

对于：
$$
f_{l,r}=\min_{k=l}^{r-1}{f_{l,k}+f_{k+1,r}}+w[l,r]~~~~~(1\leq l<r\leq n)
$$
当 $w[l,r]$ 满足两个性质时，记 $t(l,r)$ 为 $f(l,r)$ 的最优转移点：

t[l][r-1]<=k<=t[l+1][r]

$O(n^3) \rightarrow O(n^2)$。

性质：

• 对于区间包含关系具有单调性。对于任意 $l\leq l' \leq r' \leq r$，有 $w[l',r']\leq w[l,r]$。
• 四边形不等式。对于任意 $l1\leq l2 \leq r1\leq r2$，有 $w[l1,r1]+w[l2,r2]\leq w[l1,r2]+w[l2,r1]$。（交叉小于包含）。

引理1:若 $w(l,r)$ 满足区间包含单调性和四边形不等式，则状态 $f(l,r)$ 满足四边形不等式，$f(l1,r1)+f(l2,r2)\leq f(l1,r2)+f(l2,r1)$。