js 小数运算出现误差的原因
问题
在javascript使用小数点 +-*/ 运算会出现误差，比如：
0.1 + 0.2 == 0.30000000000000004
0.2 + 0.4 == 0.6000000000000001
19.9 * 100 == 1989.9999999999998
其实，不仅仅只有javascript，还有java、python等都会有类似问题，因为浮点数IEEE754是被普遍使用的标准
浮点数
浮点数是相对于定点数来说的。
计算机中小数的表示法，有定点和浮点两种。
定点，即小数点固定，比如：302876512411.25 小数点固定在数字的个位数右边
浮点，即小数点不固定（浮动），3.028e+11 小数点不固定在个位数和小数之间，而是根据指数值进行前后浮动
可以这么理解，科学记数法就是浮点数的表示方式
那么，我们为什么要使用浮点数呢？
我们可以先考虑下，为什么要使用科学记数法？
302876512411.25
3.028e+11
科学记数法的核心就是：通过移动小数点，只在小数点前保留一位数字，其他都算作小数，并使用指数记录小数点移动的位数
好处是，通过指数就可以很直观的看出数值的大小（而不用个十百千万的数）
其实它还有另一个好处，如果省略小数点后几位的话，它会显得很廋，不像原值那么臃肿（缺点是精度丢失）
计算机中的浮点数
因为计算机中，数值的存储是有大小限制的，比如
单精度浮点数 float -- 4Byte -- 32bit
双精度浮点数 double -- 8Byte -- 64bit
问题： 如何在有限的存储空间内容，尽可能的表示更多的数值？
使用定点数（原值），虽然保留了精度，但是能够表示的数值范围有限
使用浮点数（科学记数法），能够表示的数值范围变广了，但是精度也丢失了
也就是说，相同位数下
范围和精度是不可兼得
两害相权取其轻，微小的精度 没有 数值表示范围 显得更重要
所以计算机中表示小数的方式就是使用了浮点数，也就有了 IEEE754标准
二进制的定点和浮点
定点数： 以32位存储为例 （124 + 1*2e-2）
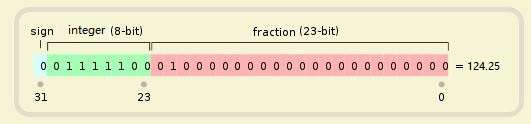
图片来源： https://www.zhihu.com/question/19848808
浮点数：(1.01)2 = 1.25 即 1.25 * 2e-3
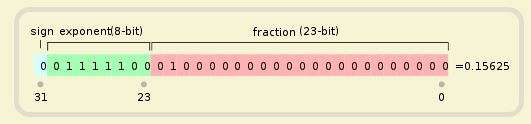
图片来源： https://www.zhihu.com/question/19848808
阶码=阶码真值+127。 （127是单精度浮点的偏移量，即 0111 1111）
IEEE 754
浮点数的存储格式，一般按照标准IEEE 754。
IEEE 754 规定，浮点数的表示方法为：
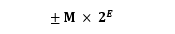
最高的 1 位是符号位 s，（表示正负）
接着的 8 位是阶码真值E，（补码，计算真值需要加上偏移量）
剩下的 23 位为尾数 M。（原码）
即
float： 1 + 8 + 23 = 32
double: 1 + 11 + 52 = 64
例如：0.125 DEC = 1/8 = 0.001 BIN = 1 x 2^-3
= 0 + 0111 1100 + 0000 0000 0000 0000 0000 000 = 00111110000000000000000000000000
IEEE754换算工具： http://www.binaryconvert.com/convert_double.html
浮点数加减乘除运算出现误差的原因
0.125 = 1/8
0.0625 = 1/16
0.03125 = 1/32
0.015625 = 1/64
0.0078125 = 1/128
0.00390625 = 1/256
0.1 = 0/2 + 0/4 + 0/8 + 1/16 + 1/32 + 0/64 + 0/128 + 1/256 + 1/512 + ...
0.1 = 0.0001 1001 1001 ...
0.2 = 0/2 + 0/4 + 1/8 + 1/16 + 0/32 + 0/64 + 1/128 + 1/256 + 0/512 + ...
0.1 = 0.0011 0011 0011 ...
原因： 一个能准确表示的十进制小数，而二进制却是循环小数
解决方法
避免使用会清除小数的换算方式
Math.floor
Math.ceil
对于整数，一般不会出错
对于小数，出错的概率较高，可以先变为整数，再缩为小数 (0.1*10 + 0.2*10) / 10 == 0.3
小数的加减乘除运算可以封装方法： https://blog.51cto.com/xzllff/831241
