数据挖掘之一元线性回归 python代码
预测结果展示 :
初始数据 : 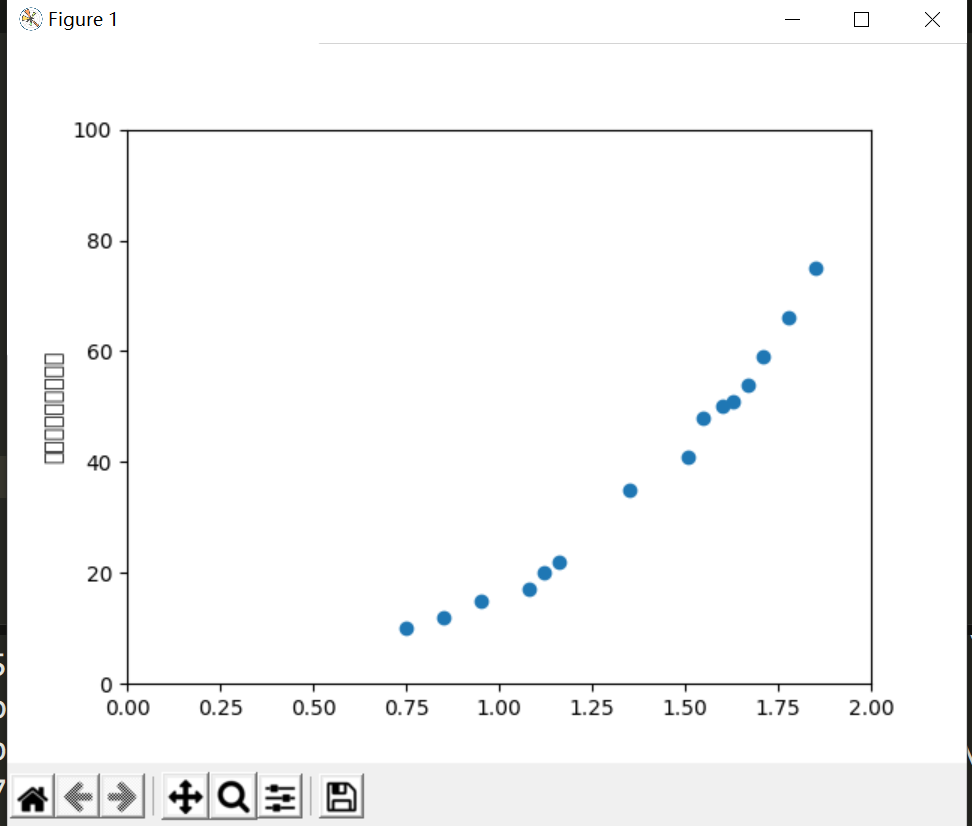
决定预测结果的是初始数据,初始数据找得好,结果就模拟的更好,我的数据找的不太好,大家可以更换好的数据测试
import matplotlib.pyplot as plt
import numpy as np
数据集x,y x,y 都是向量
给个实例x是身高(m),y是体重(kg)
我们给实际数据x,y训练出最佳的模型 y=ax+b 然后在找个身高x预测体重y
x=[0.75,0.85,0.95,1.08,1.12,1.16,1.35,1.51,1.55,1.6,1.63,1.67,1.71,1.78,1.85]
y=[10,12,15,17,20,22,35,41,48,50,51,54,59,66,75]
把x,y变成矩阵
x=np.array(x)
y=np.array(y)
把x,y数据绘制成散点图
plt.scatter(x,y)
plt.axis([0,2,0,100]) #axis传入坐标轴x,y的起点和终点
plt.ylabel("身高和体重的散点图") #标签
plt.show()
计算x,y的算数平均数 因为后边要用求a,b
x_mean = np.mean(x)
y_mean = np.mean(y)
print(x_mean,y_mean)
训练部分
num = 0.0
d = 0.0
for x_i,y_i in zip(x,y):
#a的分子
num +=(x_i - x_mean) *(y_i-y_mean)
#a的分母
d +=(x_i - x_mean)**2
a = num / d
b = y_mean - a * x_mean
预测 输入任意x 这里我采用输入一个随机数组
t = np.random.uniform(0,2)
g = a * t + b
print("输入的x是:",t)
print("预测的体重y是:",g)
print(a,b)


