- 栅格网络流
★★☆ 输入文件:flowa.in 输出文件:flowa.out 简单对比
时间限制:1 s 内存限制:128 MB
【问题描述】
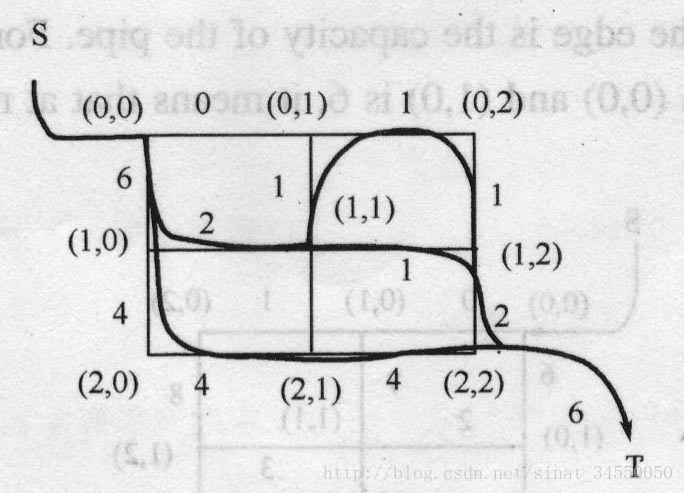
Bob 觉得一般图的最大流问题太难了,他不知道如何解决,于是他想尝试一个简单点的:栅格网络中的最大流问题,这个虽说简单了一点,但对 Bob 来说依旧太难,现在他有个麻烦需要你帮忙:给你一个 N*M 的栅格(如下所示),栅格中的边表示可以流水的管道,边上的数字表示管道的容量,举例说明:在下面图( 2.6.1 )中, (0,0) 和 (1,0) 之间边的容量为 6 ,这意味着这条边(水管)的最大水流量不超过 6 个单位。

N=3 M=3
图 2.6.1 栅格网络流
那么栅格中从 S 到 T 的最大流是多少呢 ? 换句话说 , 某一时刻最多能有多少单位的水从 S 流向 T?
【输入格式】
输入文件的第一行是一个正整数 T ,表示接下来有多少组测试数据。
每一组测试数据的第一行有两个正整数 N,M(1<=N,M<=100)
接着有两个矩阵H(N*(M-1)),V((N-1)*M),H[i][j]表示(i,j)->(i,j+1)的流量;
V[i][j]表示(i,j)->(i+1,j)的流量。
【输出格式】
每一组测试数据输出只有一行,包含一个整数,即从 S(0,0) 到 T(N-1,M-1) 的栅格网络的最大流,不允许出现多余的空格。
【输入样例】
输入文件名: flowa .in
1
3 3
0 1
2 3
4 5
6 7 8
9 10 11
输出文件名: flowa .out
6
提示:下图 (2.6.2) 所示即为样例中栅格中的一个最大流。
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#define MAXN 10111
#define INF 1e17
#define LL unsigned long long
using namespace std;
int n,m,cut,ans,head[MAXN],S,T,b[MAXN];;
LL dis[MAXN];
struct data{int v,next;LL c;}e[MAXN*8];
queue<int>q;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') x=x*10+ch-48,ch=getchar();
return x*f;
}
void add(int u,int v,int c)
{
e[++cut].v=v;e[cut].c=c;e[cut].next=head[u];head[u]=cut;
}
int slove(int x,int y)
{
return (x-1)*(m+1)+y;
}
void spfa(int t)
{
for(int i=S;i<=T;i++) dis[i]=INF;dis[S]=0;q.push(S);
while(!q.empty())
{
int u=q.front();q.pop();b[u]=false;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].v;
if(dis[v]>dis[u]+e[i].c)
{
dis[v]=dis[u]+e[i].c;
if(b[v]!=t) b[v]=t,q.push(v);
}
}
}
return ;
}
void Clear()
{
memset(head,0,sizeof head);
cut=0;
return ;
}
int main()
{
freopen("flowa.in","r",stdin);
freopen("flowa.out","w",stdout);
int t,x;t=read();
while(t--)
{
Clear();
n=read(),m=read();
S=0,T=(n+1)*(m+1)+1;
for(int i=1;i<=n;i++)
for(int j=2;j<=m;j++)
{
x=read();
add(slove(i,j),slove(i+1,j),x);
add(slove(i+1,j),slove(i,j),x);
}
for(int i=2;i<=n;i++)
for(int j=1;j<=m;j++)
{
x=read();
add(slove(i,j),slove(i,j+1),x);
add(slove(i,j+1),slove(i,j),x);
}
for(int i=2;i<=m;i++) add(S,i,0);
for(int i=2*(m+1);i<=T-2;i+=(m+1)) add(S,i,0);
for(int i=m+2;i<=T-2;i+=(m+1)) add(i,T,0);
for(int i=n*(m+1)+2;i<=T-2;i++) add(i,T,0);
spfa(t+1);cout<<dis[T]<<endl;
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号