红黑树原理和算法介绍
转载 红黑树(一)之 原理和算法详细介绍 30 张图带你彻底理解红黑树
一、红黑树介绍
什么是红黑树?
红黑树是一种自平衡二叉查找树,是计算机科学领域中的一种数据结构,典型的用途是实现关联数组,存储有序的数据。它是在1972年由Rudolf Bayer发明的,别称"对称二叉B树",它现代的名字由 Leo J. Guibas 和 Robert Sedgewick 于1978年写的一篇论文中获得的。它是复杂的,但它的操作有着良好的最坏情况运行时间,并且在实践中是高效的。它可以在O(logn)时间内做查找,插入和删除,这里的n是树的结点个数。
红黑树和平衡二叉树(AVL树)都是二叉查找树的变体,但红黑树的统计性能要好于AVL树。因为,AVL树是严格维持平衡的,红黑树是黑平衡的。维持平衡需要额外的操作,这就加大了数据结构的时间复杂度,所以红黑树可以看作是二叉搜索树和AVL树的一个折中,维持平衡的同时也不需要花太多时间维护数据结构的性质。红黑树在很多地方都有应用,例如:
- C++的STL,map和set都是用红黑树实现的。
- 著名的linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块。
- epoll在内核中的实现,用红黑树管理事件块。
- nginx用红黑树管理timer等。
- Java的TreeMap实现。
红黑树简介:
R-B Tree,全称是Red-Black Tree,又称为“红黑树”,是一种特殊的二叉查找树。红黑树的每个结点上都有存储位表示结点的颜色,可以是红(Red)或黑(Black)。
红黑树的特性:
- 每个结点是黑色或者红色。
- 根结点是黑色。
- 每个叶子结点(NIL)是黑色。 [注意:这里叶子结点,是指为空(NIL或NULL)的叶子结点!]
- 如果一个结点是红色的,则它的子结点必须是黑色的。
- 每个结点到叶子结点NIL所经过的黑色结点的个数一样的。[确保没有一条路径会比其他路径长出俩倍,所以红黑树是相对接近平衡的二叉树的!]
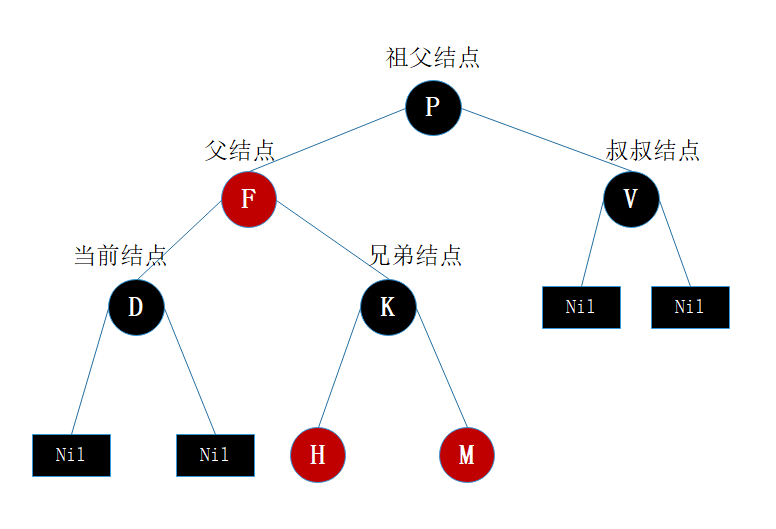
图1(红黑树)
二、红黑树基本操作
红黑树的基本操作是添加、删除。在对红黑树进行添加或删除之后,都会用到旋转方法。为什么呢?道理很简单,添加或删除红黑树中的结点之后,红黑树的结构就发生了变化,可能不满足红黑树的5条性质,也就不再是一颗红黑树了,而是一颗普通的树。而通过旋转和变色,可以使这颗树重新成为红黑树。简单点说,旋转和变色的目的是让树保持红黑树的特性:自平衡二叉树。
旋转包括两种:左旋 和 右旋。下面分别对它们进行介绍:
左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,其左子结点保持不变。如图2。
右旋:以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,其右子结点保持不变。如图3。
变色:结点的颜色由红变黑或由黑变红。
1.左旋
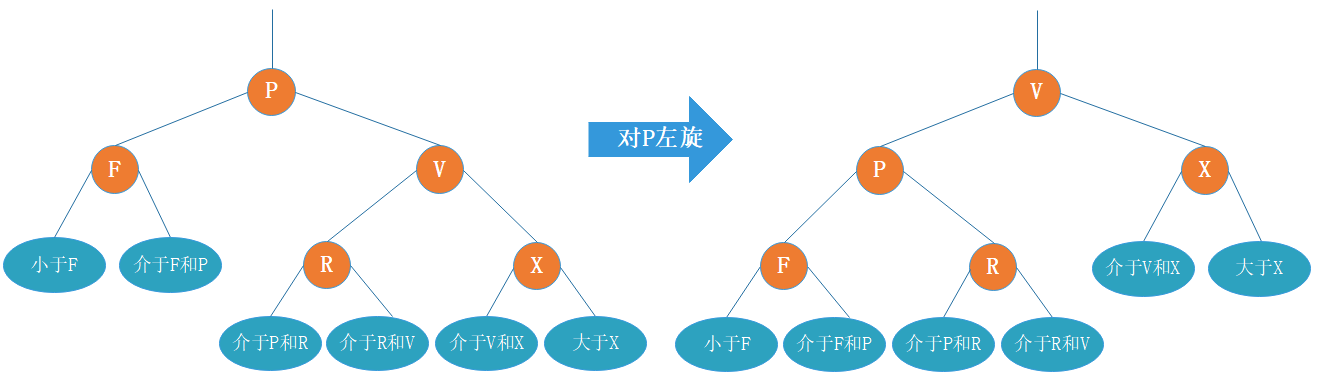
图2(左旋图)
左旋算法:
LEFT-ROTATE(T, x) y ← right[x] // 前提:这里假设x的右孩子为y。下面开始正式操作 right[x] ← left[y] // 将 “y的左孩子” 设为 “x的右孩子” p[left[y]] ← x // 将 “x” 设为 “y的左孩子的父亲” p[y] ← p[x] // 将 “x的父亲” 设为 “y的父亲” if p[x] = nil[T] then root[T] ← y // 情况1:如果 “x的父亲” 是空节点,则将y设为根节点 else if x = left[p[x]] then left[p[x]] ← y // 情况2:如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子” else right[p[x]] ← y // 情况3:(x是它父节点的右孩子) 将y设为“x的父节点的右孩子” left[y] ← x // 将 “x” 设为 “y的左孩子” p[x] ← y // 将 “x的父节点” 设为 “y”
2.右旋

图3(右旋图)
右旋算法:
RIGHT-ROTATE(T, y) x ← left[y] // 前提:这里假设y的左孩子为x。下面开始正式操作 left[y] ← right[x] // 将 “x的右孩子” 设为 “y的左孩子” p[right[x]] ← y // 将 “y” 设为 “x的右孩子的父亲” p[x] ← p[y] // 将 “y的父亲” 设为 “x的父亲” if p[y] = nil[T] then root[T] ← x // 情况1:如果 “y的父亲” 是空结点,则将x设为根结点 else if y = right[p[y]] then right[p[y]] ← x // 情况2:如果 y是它父结点的右孩子,则将x设为“y的父结点的左孩子” else left[p[y]] ← x // 情况3:(y是它父结点的左孩子) 将x设为“y的父结点的左孩子” right[x] ← y // 将 “y” 设为 “x的右孩子” p[y] ← x // 将 “y的父结点” 设为 “x”
我们先忽略颜色,可以看到旋转操作不会影响旋转结点的父结点,父结点以上的结构还是保持不变的。
左旋只影响旋转结点和其右子树的结构,把右子树的结点往左子树挪了。
右旋只影响旋转结点和其左子树的结构,把左子树的结点往右子树挪了。
所以旋转操作是局部的。另外可以看出旋转能保持红黑树平衡的一些端详了:当一边子树的结点少了,那么向另外一边子树“借”一些结点;当一边子树的结点多了,那么向另外一边子树“租”一些结点。
但要保持红黑树的性质,结点不能乱挪,还得靠变色了。怎么变?具体情景又不同变法,后面会具体讲到,现在只需要记住红黑树总是通过旋转和变色达到自平衡。
3.添加
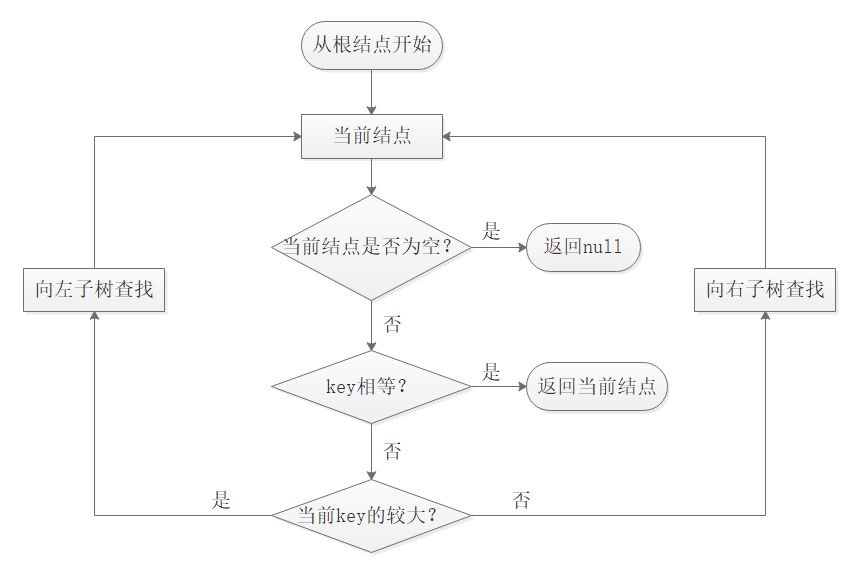
图4(插入结点流程图)
插入算法:
RB-INSERT(T, z) y ← nil[T] // 新建结点“y”,将y设为空结点。 x ← root[T] // 设“红黑树T”的根结点为“x” while x ≠ nil[T] // 找出要插入的结点“z”在二叉树T中的位置(父结点),即“y”结点要存放的位置 do y ← x if key[z] < key[x] then x ← left[x] else x ← right[x] p[z] ← y // 设置 “z的父亲” 为 “y” if y = nil[T] then root[T] ← z // 情景1:若y是空结点,则将z设为根结点 else if key[z] < key[y] then left[y] ← z // 情景2:若“z的key值” < “y的key值”,则将z设为“y的左孩子” else right[y] ← z // 情景2:若“z的key值” >= “y的key值”,则将z设为“y的右孩子” left[z] ← nil[T] // z的左孩子设为空 right[z] ← nil[T] // z的右孩子设为空。至此,已经完成将“结点z插入到二叉树”中了。 color[z] ← RED // 将z着色为“红色” RB-INSERT-FIXUP(T, z) // 通过RB-INSERT-FIXUP对红黑树的结点进行颜色修改以及旋转,让树T仍然是一颗红黑树
插入修正算法:
RB-INSERT-FIXUP(T, z) while color[p[z]] = RED // 若“当前结点(z)的父结点是红色”,则进行以下处理。 do if p[z] = left[p[p[z]]] // 若“z的父结点”是“z的祖父结点的左孩子”,则进行以下处理。 then y ← right[p[p[z]]] // 将y设置为“z的叔叔结点(z的祖父结点的右孩子)” if color[y] = RED // 4.1情景:叔叔是红色 then color[p[z]] ← BLACK // (01) 将“父结点”设为黑色。 color[y] ← BLACK // (02) 将“叔叔结点”设为黑色。 color[p[p[z]]] ← RED // (03) 将“祖父结点”设为“红色”。 z ← p[p[z]] // (04) 将“祖父结点”设为“当前结点”(红色结点) else if z = right[p[z]] // 4.3.1情景:叔叔是黑色,且当前结点是右孩子 then z ← p[z] // (01) 将“父结点”作为“新的当前结点”。 LEFT-ROTATE(T, z) // (02) 以“新的当前结点”为支点进行左旋。 color[p[z]] ← BLACK // 4.2.1情景:叔叔是黑色,且当前结点是左孩子。(01) 将“父结点”设为“黑色”。 color[p[p[z]]] ← RED // (02) 将“祖父结点”设为“红色”。 RIGHT-ROTATE(T, p[p[z]]) // (03) 以“祖父结点”为支点进行右旋。 else (same as then clause with "right" and "left" exchanged) // 若“z的父结点”是“z的祖父结点的右孩子”,将上面的操作中“right”和“left”交换位置,然后依次执行。 color[root[T]] ← BLACK // 情景1:若y是空结点,则将z设为根结点
但插入结点是为什么是红色呢?理由很简单,红色在父结点(如果存在)为黑色结点时,红黑树的黑色平衡没被破坏,不需要做自平衡操作。但如果插入结点是黑色,那么插入位置所在的子树黑色结点总是多1,必须做自平衡。
插入情况可以总结为下面这些:
情景1:
红黑树为空树
最简单的一种情景,直接把插入结点作为根结点就行,但注意,根据红黑树性质2:根结点是黑色。所以还需要把插入结点设为黑色。
处理:
- 把插入结点作为根结点,并把结点设置为黑色。
情景2:
插入结点的Key已存在
插入结点的Key已存在,因为红黑树总保持平衡,在插入前红黑树已经是平衡的,那么把插入结点设置为将要替代的结点颜色,再把结点的值更新就完成插入了。
处理:
- 把z设为当前结点的颜色。
- 更新当前结点的值为插入结点的值。
情景3:
插入结点的父结点为黑结点
由于插入的结点是红色的,并不会影响红黑树的平衡,直接插入即可,无需做自平衡。
处理:
- 直接插入。
情景4:
插入结点的父结点为红结点
再次回想下红黑树的性质2:根结点是黑色。如果插入的父结点为红结点,那么该父结点不可能为根结点,所以插入结点总是存在祖父结点。这点很重要,因为后续的旋转操作需要祖父结点的参与。
情景4.1:
叔叔结点存在并且为红结点
从红黑树性质4可以确定,祖父结点为黑结点,因为不可以同时存在两个相连的红结点。那么此时该插入子树的红黑层数的情况是:黑红红。显然最简单的处理方式是把其改为:红黑红。如图5和图6所示。
处理:
- 将P和S设置为黑色(当前插入结点I)
- 将PP设置为红色
- 把PP设置为当前插入结点

图5

图6
红黑树的生长是自底向上的。这点不同于普通的二叉查找树,普通的二叉查找树的生长是自顶向下的。
情景4.2:
叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的左子结点
单纯从插入前来看,也即不算情景4.1自底向上处理时的情况,叔叔结点非红即为叶子结点(Nil)。因为如果叔叔结点为黑结点,而父结点为红结点,那么叔叔结点所在的子树的黑色结点就比父结点所在子树的多了,这不满足红黑树的性质5。后续情景同样如此,不再多做说明了。
情景4.2.1:
插入结点是其父结点的左子结点
处理:
- 将P设为黑色
- 将PP设为红色
- 对PP进行右旋
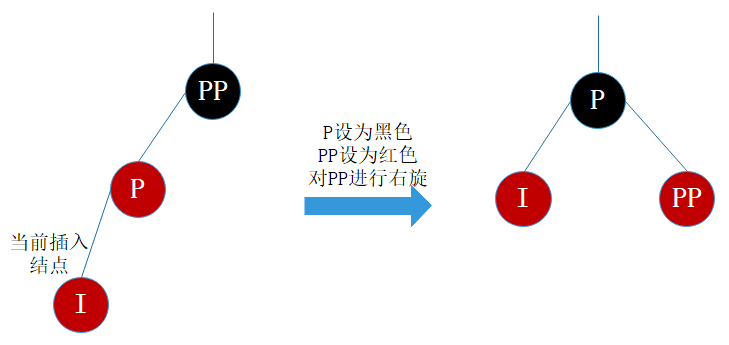
图7
咦,可以把PP设为红色,I和P设为黑色吗?答案是可以!看过《算法:第4版》的同学可能知道,书中讲解的就是把PP设为红色,I和P设为黑色。但把PP设为红色,显然又会出现情景4.1的情况,需要自底向上处理,做多了无谓的操作,既然能自己消化就不要麻烦祖辈们啦~
情景4.2.2:
插入结点是其父结点的右子结点
这种情景显然可以转换为情景4.2.1,如图12所示,不做过多说明了。
处理:
- 对P进行左旋
- 把P设置为插入结点,得到情景4.2.1
- 进行情景4.2.1的处理
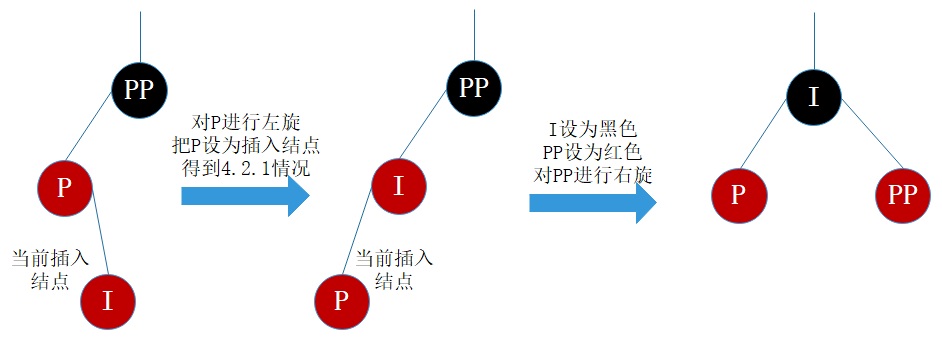
图8
情景4.3:
叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的右子结点
该情景对应情景4.2,只是方向反转,不做过多说明了,直接看图。
情景4.3.1:
插入结点是其父结点的右子结点
处理:
- 将P设为黑色
- 将PP设为红色
- 对PP进行左旋
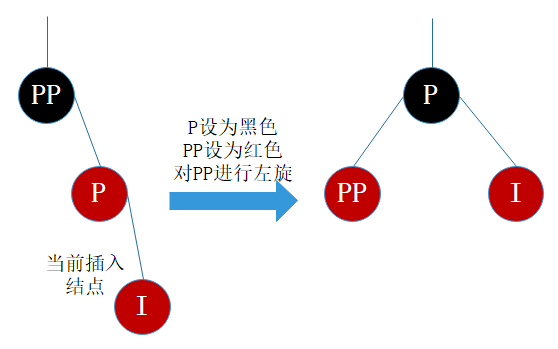
图9
情景4.3.2:
插入结点是其父结点的左子结点
处理:
- 对P进行右旋
- 把P设置为插入结点,得到情景4.3.1
- 进行情景4.3.1的处理

图10
4.删除
红黑树的删除操作包括两部分工作:
- 查找目标结点。
- 删除结点后自平衡。
查找目标结点显然可以复用查找操作,当不存在目标结点时,忽略本次操作;当存在目标结点时,删除后需要做自平衡处理。删除结点后我们需要找结点来替代删除结点的位置,不然子树跟父辈结点断开了,除非删除结点刚好没子结点,那么就不需要替代。
二叉树删除结点找替代结点有3种情情景:
情景1:若删除结点无子结点,直接删除。
情景2:若删除结点只有一个子结点,用子结点替换删除结点。
情景3:若删除结点有两个子结点,用后继结点(大于删除结点的最小结点)替换删除结点。
情景3中可以用前继结点(小于删除结点的最大结点)替代删除结点吗?可以的。但习惯上大多都是拿后继结点来替代,后文的讲解也是用后继结点来替代。另外告诉大家一种找前继和后继结点的直观的方法(不知为何没人提过,大家都知道?):把二叉树所有结点投射在X轴上,所有结点都是从左到右排好序的,所有目标结点的前后结点就是对应的前继和后继结点。如图11所示。
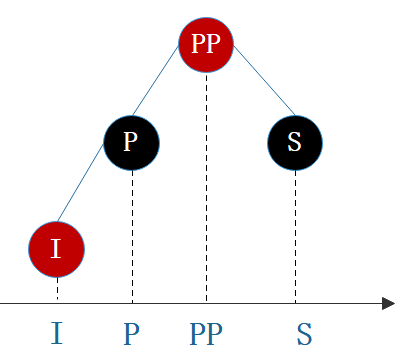
图11
接下来,讲一个重要的思路:删除结点被替代后,在不考虑结点的键值的情况下,对于树来说,可以认为删除的是替代结点!话很苍白,我们看图12。在不看键值对的情况下,图12的红黑树最终结果是删除了Q所在位置的结点!这种思路非常重要,大大简化了后文讲解红黑树删除的情景!

图12
基于此,上面所说的3种二叉树的删除情景可以相互转换并且最终都是转换为情景1!!
情景2:删除结点用其唯一的子结点替换,子结点替换为删除结点后,可以认为删除的是子结点,若子结点又有两个子结点,那么相当于转换为情景3,一直自顶向下转换,总是能转换为情景1。(根据红黑树的性质来说,只存在一个子结点的结点肯定在树末了)
情景3:删除结点用后继结点(后继结点肯定不存在左结点),如果后继结点有右子结点,那么相当于转换为情景2,否则转为为情景1。

图13
删除算法:
RB-DELETE(T, z) if left[z] = nil[T] or right[z] = nil[T] then y ← z // 若“z的左孩子” 或 “z的右孩子”为空,则将“z”赋值给 “y”; else y ← TREE-SUCCESSOR(z) // 否则,将“z的后继节点”赋值给 “y”。 if left[y] ≠ nil[T] then x ← left[y] // 若“y的左孩子” 不为空,则将“y的左孩子” 赋值给 “x”; else x ← right[y] // 否则,“y的右孩子” 赋值给 “x”。 p[x] ← p[y] // 将“y的父节点” 设置为 “x的父节点” if p[y] = nil[T] then root[T] ← x // 若“y的父节点” 为空,则设置“x” 为 “根节点”。 else if y = left[p[y]] then left[p[y]] ← x // 若“y是它父节点的左孩子”,则设置“x” 为 “y的父节点的左孩子” else right[p[y]] ← x // 若“y是它父节点的右孩子”,则设置“x” 为 “y的父节点的右孩子” if y ≠ z then key[z] ← key[y] // 若“y的值” 赋值给 “z”。注意:这里只拷贝z的值给y,而没有拷贝z的颜色!!! copy y's satellite data into z if color[y] = BLACK then RB-DELETE-FIXUP(T, x) // 若“y为黑节点”,即替换结点是黑色则调用删除修正算法 return y
删除修正算法:
删除修正算法: RB-DELETE-FIXUP(T, x) while x ≠ root[T] and color[x] = BLACK do if x = left[p[x]] then w ← right[p[x]] // 若 “x”是“它父节点的左孩子”,则设置 “w”为“x的兄弟”(即x为它父节点的右孩子) if color[w] = RED // 情景2.1.1: x是“黑+黑”节点,x的兄弟节点是红色。(此时x的父节点和x的兄弟节点的子节点都是黑节点)。 then color[w] ← BLACK // (01) 将x的兄弟节点设为“黑色”。 color[p[x]] ← RED // (02) 将x的父节点设为“红色”。 LEFT-ROTATE(T, p[x]) // (03) 对x的父节点进行左旋。 w ← right[p[x]] // (04) 左旋后,重新设置x的兄弟节点。 if color[left[w]] = BLACK and color[right[w]] = BLACK // 情景2.1.2.3: x是“黑+黑”节点,x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色。 then color[w] ← RED // (01) 将x的兄弟节点设为“红色”。 x ← p[x] // (02) 设置“x的父节点”为“新的x节点”。 else if color[right[w]] = BLACK // 情景2.1.2.2: x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的。 then color[left[w]] ← BLACK // (01) 将x兄弟节点的左孩子设为“黑色”。 color[w] ← RED // (02) 将x兄弟节点设为“红色”。 RIGHT-ROTATE(T, w) // (03) 对x的兄弟节点进行右旋。 w ← right[p[x]] // (04) 右旋后,重新设置x的兄弟节点。 color[w] ← color[p[x]] // 情景2.1.2.1: x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的。(01) 将x父节点颜色 赋值给 x的兄弟节点。 color[p[x]] ← BLACK // (02) 将x父节点设为“黑色”。 color[right[w]] ← BLACK // (03) 将x兄弟节点的右子节设为“黑色”。 LEFT-ROTATE(T, p[x]) // (04) 对x的父节点进行左旋。 x ← root[T] // (05) 设置“x”为“根节点”。 else (same as then clause with "right" and "left" exchanged) // 若 “x”是“它父节点的右孩子”,将上面的操作中“right”和“left”交换位置,然后依次执行。 color[x] ← BLACK
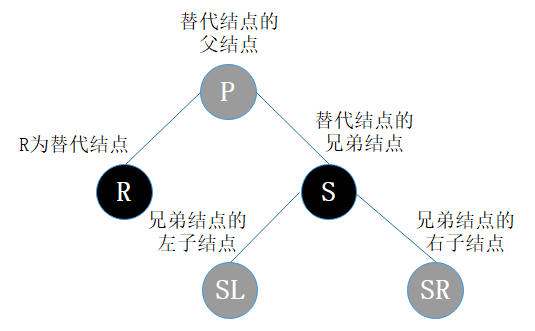
图14
图中字母并不代表结点Key的大小。R表示替代结点,P表示替代结点的父结点,S表示替代结点的兄弟结点,SL表示兄弟结点的左子结点,SR表示兄弟结点的右子结点。灰色结点表示它可以是红色也可以是黑色。
值得特别提醒的是,R是即将被替换到删除结点的位置的替代结点,在删除前,它还在原来所在位置参与树的子平衡,平衡后再替换到删除结点的位置,才算删除完成。
删除情况可以总结为下面这些:
情景1:
替换结点是红色结点
我们把替换结点换到了删除结点的位置时,由于替换结点是红色,删除也了不会影响红黑树的平衡,只要把替换结点的颜色设为删除的结点的颜色即可重新平衡。如图12。
处理:
- 颜色变为删除结点的颜色
情景2:
替换结点是黑结点
当替换结点是黑色时,我们就不得不进行自平衡处理了。我们必须还得考虑替换结点是其父结点的左子结点还是右子结点,来做不同的旋转操作,使树重新平衡。
情景2.1:
替换结点是其父结点的左子结点
情景2.1.1:
替换结点的兄弟结点是红结点
若兄弟结点是红结点,那么根据性质4,兄弟结点的父结点和子结点肯定为黑色,不会有其他子情景,我们按图15处理,得到情景2.1.2.3(后续讲解,这里先记住,此时R仍然是替代结点,它的新的兄弟结点SL和兄弟结点的子结点都是黑色)。
处理:
- 将S设为黑色
- 将P设为红色
- 对P进行左旋,得到情景2.1.2.3
- 进行情景2.1.2.3的处理
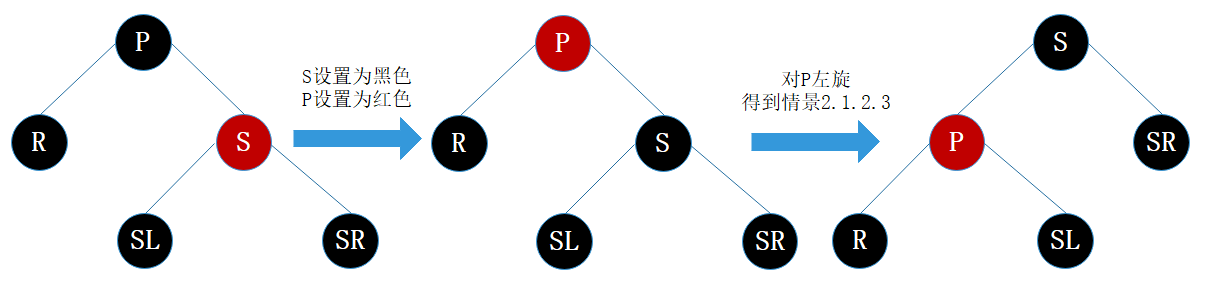
图15
情景2.1.2:
替换结点的兄弟结点是黑结点
当兄弟结点为黑时,其父结点和子结点的具体颜色也无法确定(如果也不考虑自底向上的情况,子结点非红即为叶子结点Nil,Nil结点为黑结点),此时又得考虑多种子情景。
情景2.1.2.1:
替换结点的兄弟结点的右子结点是红结点,左子结点任意颜色
即将删除的左子树的一个黑色结点,显然左子树的黑色结点少1了,然而右子树又有红色结点,那么我们直接向右子树“借”个红结点来补充黑结点就好啦,此时肯定需要用旋转处理了。如图16所示。
处理:
- 将S的颜色设为P的颜色
- 将P设为黑色
- 将SR设为黑色
- 对P进行左旋
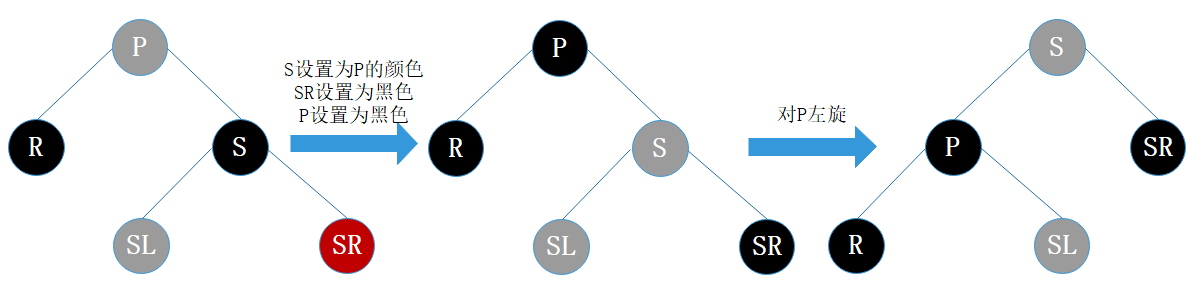
图16
平衡后的图怎么不满足红黑树的性质?前文提醒过,R是即将替换的,它还参与树的自平衡,平衡后再替换到删除结点的位置,所以R最终可以看作是删除的。另外图15是考虑到第一次替换和自底向上处理的情况,如果只考虑第一次替换的情况,根据红黑树性质,SL肯定是红色或为Nil,所以最终结果树是平衡的。如果是自底向上处理的情况,同样,每棵子树都保持平衡状态,最终整棵树肯定是平衡的。后续的情景同理,不做过多说明了。
情景2.1.2.2:
替换结点的兄弟结点的右子结点为黑结点,左子结点为红结点
兄弟结点所在的子树有红结点,我们总是可以向兄弟子树借个红结点过来,显然该情景可以转换为情景2.1.2.1。如图17所示。
处理:
- 将S设为红色
- 将SL设为黑色
- 对S进行右旋,得到情景2.1.2.1
- 进行情景2.1.2.1的处理
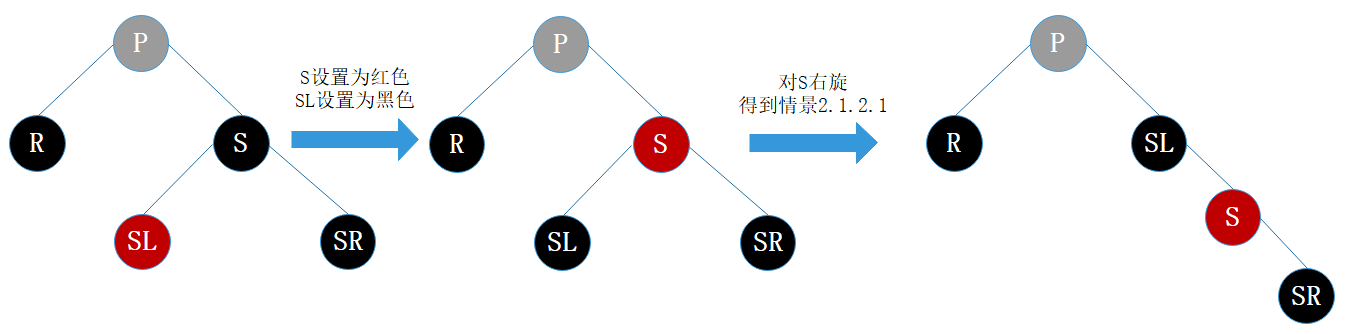
图17
删除情景2.1.2.3:
替换结点的兄弟结点的子结点都为黑结点
好了,此次兄弟子树都没红结点“借”了,兄弟帮忙不了,找父母呗,这种情景我们把兄弟结点设为红色,再把父结点当作替代结点,自底向上处理,去找父结点的兄弟结点去“借”。但为什么需要把兄弟结点设为红色呢?显然是为了在P所在的子树中保证平衡(R即将删除,少了一个黑色结点,子树也需要少一个),后续的平衡工作交给父辈们考虑了,还是那句,当每棵子树都保持平衡时,最终整棵总是平衡的。
处理:
- 将S设为红色
- 把P作为新的替换结点
- 重新进行删除结点情景处理

图18
删除情景2.2:
替换结点是其父结点的右子结点
好啦,右边的操作也是方向相反,不做过多说明了,相信理解了删除情景2.1后,肯定可以理解2.2。
删除情景2.2.1:
替换结点的兄弟结点是红结点
处理:
- 将S设为黑色
- 将P设为红色
- 对P进行右旋,得到情景2.2.2.3
- 进行情景2.2.2.3的处理
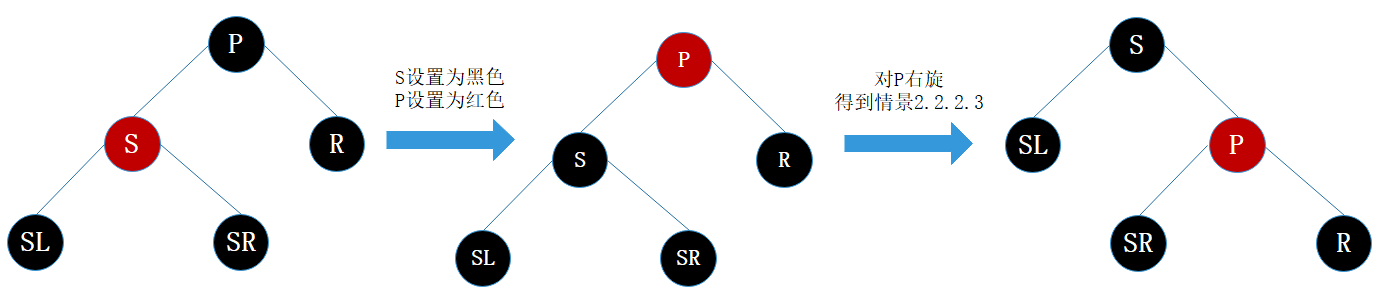
图19
删除情景2.2.2:
替换结点的兄弟结点是黑结点
删除情景2.2.2.1:
替换结点的兄弟结点的左子结点是红结点,右子结点任意颜色
处理:
- 将S的颜色设为P的颜色
- 将P设为黑色
- 将SL设为黑色
- 对P进行右旋
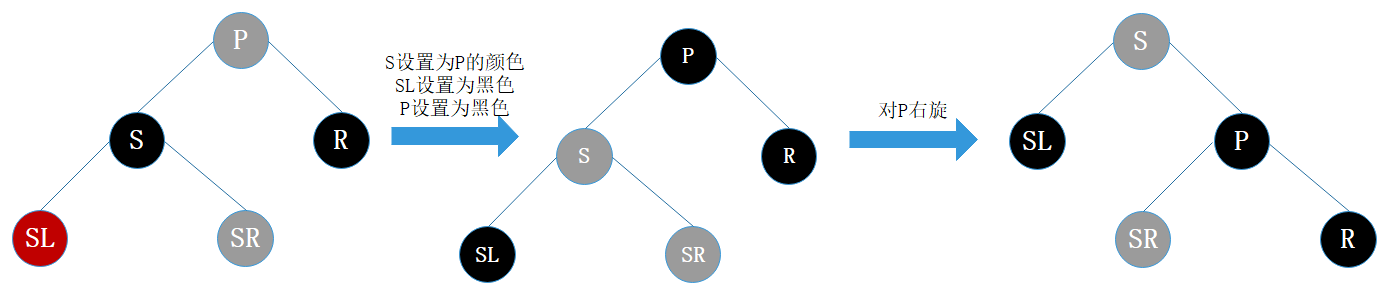
图20
删除情景2.2.2.2:
替换结点的兄弟结点的左子结点为黑结点,右子结点为红结点
处理:
- 将S设为红色
- 将SR设为黑色
- 对S进行左旋,得到情景2.2.2.1
- 进行情景2.2.2.1的处理

图21
删除情景2.2.2.3:
替换结点的兄弟结点的子结点都为黑结点
处理:
- 将S设为红色
- 把P作为新的替换结点
- 重新进行删除结点情景处理
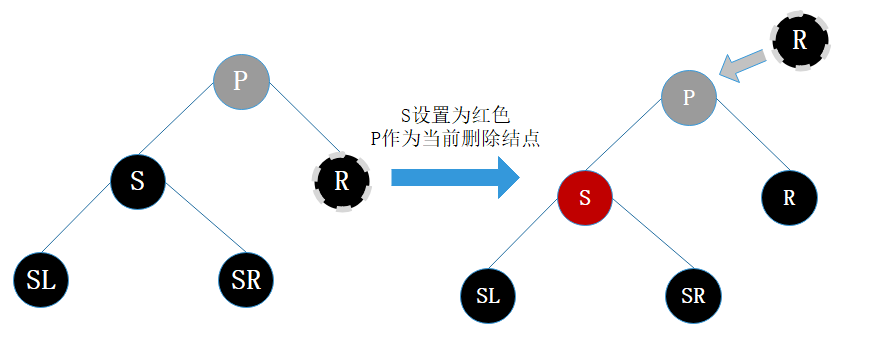
图22
综上,红黑树删除后自平衡的处理可以总结为:
- 自己能搞定的自消化(情景1)
- 自己不能搞定的叫兄弟帮忙(除了情景1、情景2.1.2.3和情景2.2.2.3)
- 兄弟都帮忙不了的,通过父母,找远方亲戚(情景2.1.2.3和情景2.2.2.3)
哈哈,是不是跟现实中很像,当我们有困难时,首先先自己解决,自己无力了总兄弟姐妹帮忙,如果连兄弟姐妹都帮不上,再去找远方的亲戚了。这里记忆应该会好记点~




