多分类的评价指标PRF(Macro-F1/MicroF1/weighted)详解
也许是由于上学的时候一直搞序列标注任务,多分类任务又可以简化为简单的二分类任务,所以一直认为PRF值很简单,没啥好看的。然鹅,细看下来竟有点晦涩难懂,马篇博留个念咯~
前言
PRF值分别表示准确率(Precision)、召回率(Recall)和F1值(F1-score),有机器学习基础的小伙伴应该比较熟悉。
根据标题,先区别一下“多分类”与“多标签”:
多分类:表示分类任务中有多个类别,但是对于每个样本有且仅有一个标签,例如一张动物图片,它只可能是猫,狗,虎等中的一种标签(二分类特指分类任务中只有两个类别)
多标签:一个样本可以有多个标签。例如文本分类中,一个文本可以是宗教相关,也可以是新闻相关,所以它就可以有两个标签
想要详细了解可以参考博客 https://blog.csdn.net/lyy14011305/article/details/88664518
此处只介绍多分类任务的评价指标~
混淆矩阵与PRF值
1. 混淆矩阵
混淆矩阵是数据科学和机器学习中经常使用的用来总结分类模型预测结果的表,用n行n列的矩阵来表示,将数据集中的记录按照真实的类别和预测的类别两个标准进行汇总。以二分类任务为例,混淆矩阵的结构如下:
| 混淆矩阵 | 预测 | ||
| 真(正) | 假(负) | ||
| 实际 | 真(正) | TP | FN |
| 假(负) | FP | TN | |
其中:
TP——将正类预测为正类的个数
FN——将正类预测为负类的个数
FP——将负类预测为正类的个数
TN——将负类预测为负类的个数
2. 传统的PRF值公式
P = (预测为真且正确预测的样本数)/(所有预测为真的样本数)= TP/(TP+FP)
R = (预测为真且正确预测的样本数)/(实际情况中为真的样本数)= TP/(TP+FN)
F = 2*P*R/(P+R)
传统的PRF公式仅适用于二分类任务
3. PRF值-微平均(Micro Average)
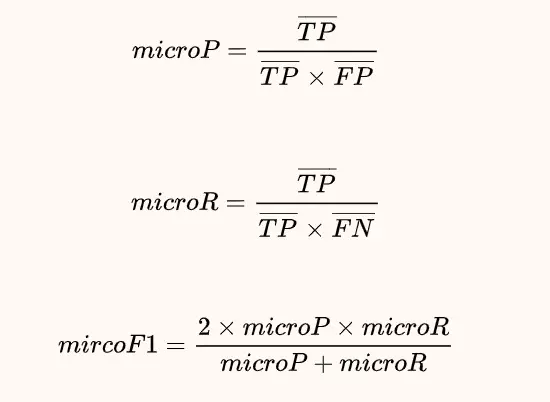
"Micro"是通过先计算总体的TP, FP和FN的数量,然后计算PRF。即先将多个混淆矩阵的TP,FP,TN,FN对应的位置求平均,然后按照PRF值公式及逆行计算。公式如下:
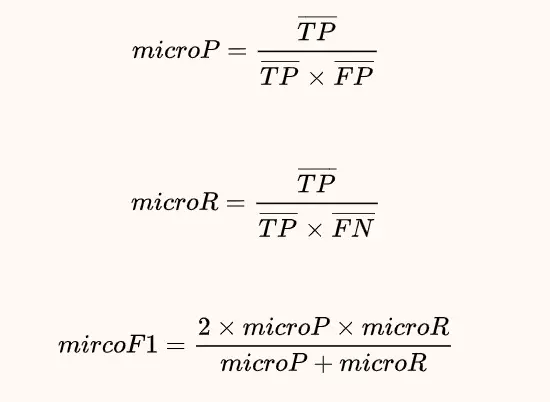
下面通过一个简单的例子来理解,假设是三个类别的分类模型:
y_true=[1,2,3]
y_pred=[1,1,3]
(1)如下,将第一个类别设置为True(1),非第一个类别设置为False(0),
y_true=[1,0,0]
y_pred=[1,1,0]
由此我们统计得到第一个类别的混淆矩阵:
| 第一类 | 预测 | ||
| 真(正) | 假(负) | ||
| 实际 | 真(正) | 1(TP) | 0(FN) |
| 假(负) | 1(FP) | 1(TN) | |
(2)如下,将第二个类别设置为True(1),非第二个类别设置为False(0),
y_true=[0,1,0]
y_pred=[0,0,0]
由此我们统计得到第二个类别的混淆矩阵:
| 第二类 | 预测 | ||
| 真(正) | 假(负) | ||
| 实际 | 真(正) | 0(TP) | 1(FN) |
| 假(负) | 0(FP) | 2(TN) | |
(3)如下,将第三个类别设置为True(1),非第三个类别设置为False(0),
y_true=[0,0,1]
y_pred=[0,0,1]
由此我们统计得到第三个类别的混淆矩阵:
| 第三类 | 预测 | ||
| 真(正) | 假(负) | ||
| 实际 | 真(正) | 1(TP) | 0(FN) |
| 假(负) | 0(FP) | 2(TN) | |
(4)根据微平均算法公式我们得到最终的混淆矩阵,如下:
| 最终 | 预测 | ||
| 真(正) | 假(负) | ||
| 实际 | 真(正) | 2/3(TP) | 1/3(FN) |
| 假(负) | 1/3(FP) | 5/3(TN) | |
带入微平均公式得:
micro-P = TP/(TP+FP) = (2/3)/(2/3 + 1/3)= 2/3
micro-R = TP/(TP+FN) = (2/3)/(2/3 + 1/3)= 2/3
micro-F1 = 2*P*R/(P+R) = 2/3
4. PRF值-宏平均(Macro Average)
“Macro”是分别计算每个类别的PRF,然后分别求平均得到PRF。即对多个混淆矩阵求PRF,然后求PRF的算术平均。公式如下:
同样借助上面例子,假设是三个类别的分类模型:(若除法过程中,分子分母同时为0,则结果也为0)
y_true=[1,2,3]
y_pred=[1,1,3]
(1)如下,将第一个类别设置为True(1),非第一个类别设置为False(0),
y_true=[1,0,0]
y_pred=[1,1,0]
由此我们统计得到第一个类别的混淆矩阵:
| 第一类 | 预测 | ||
| 真(正) | 假(负) | ||
| 实际 | 真(正) | 1(TP) | 0(FN) |
| 假(负) | 1(FP) | 1(TN) | |
我们可以计算第一个类别的PRF值如下:
- P1 = TP/(TP+FP) = 1/(1+1) = 1/2
- R1 = TP/(TP+FN) = 1/1 = 1
- F1_1 = 2*P1*R1/(P1+R1) = 2/3
(2)如下,将第二个类别设置为True(1),非第二个类别设置为False(0),
y_true=[0,1,0]
y_pred=[0,0,0]
由此我们统计得到第二个类别的混淆矩阵:
| 第二类 | 预测 | ||
| 真(正) | 假(负) | ||
| 实际 | 真(正) | 0(TP) | 1(FN) |
| 假(负) | 0(FP) | 2(TN) | |
我们可以计算第二个类别的PRF值如下:
- P2 = TP/(TP+FP) = 0
- R2 = TP/(TP+FN) = 0
- F1_2 = 2*P2*R2/(P2+R2) = 0
(3)如下,将第三个类别设置为True(1),非第三个类别设置为False(0),
y_true=[0,0,1]
y_pred=[0,0,1]
由此我们统计得到第三个类别的混淆矩阵:
| 第三类 | 预测 | ||
| 真(正) | 假(负) | ||
| 实际 | 真(正) | 1(TP) | 0(FN) |
| 假(负) | 0(FP) | 2(TN) | |
我们可以计算第三个类别的PRF值如下:
- P3 = TP/(TP+FP) = 1/1 = 1
- R3 = TP/(TP+FN) = 1/1 = 1
- F1_3 = 2*P3*R3/(P3+R3) = 1
(4)对P1, P2, P3取平均得到P, 对R1, R2, R3取平均得到R, 对F1_1, F1_2, F1_3求平均得到F1:
- P = (P1+P2+P3)/3 = (1/2 + 0 + 1/3 = 1/2
- R = (R1+R2+R3)/3=(1 +0 +1)/3 = 2/3
- F1 = 2*P*R/(P+R) = 4/7
4. PRF值-权重(Weighted)
weighted计算方法就是对于macro中的每一类的PRF给予不同的权重
本文介绍了PRF值的计算方法的公式及计算方法,希望可以帮到你~
下一篇继续更利用python实现PRF的方法~欢迎关注
参考博客:
https://blog.csdn.net/ybdesire/article/details/96507733
https://blog.csdn.net/lyb3b3b/article/details/84819931
http://www.sohu.com/a/135668355_556897
https://blog.csdn.net/qq_36426650/article/details/88073089
https://zhuanlan.zhihu.com/p/59862986
https://www.zhihu.com/question/36883196?from=profile_question_card
https://www.jianshu.com/p/100f3dee345d



