对中值定理的认识

参考：https://zhuanlan.zhihu.com/p/47436090

中值定理包含罗尔中值定理、拉格朗日中值定理和柯西中值定理。很多定理都需要以此为基础进行证明。

首先看罗尔中值定理，

举一个简单的例子，一个人从A处跑到B处。他的速度肯定是从0加速又逐渐减速到0的。将它的速度表示成一个v-t函数，应该呈现拱形。

 

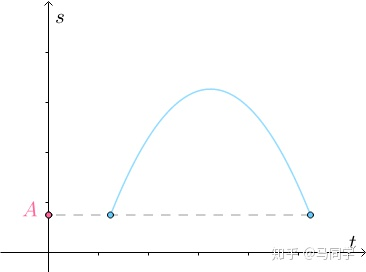
 对于这样的一个函数，中间肯定存在着v‘=0，即加速度为0的点。这就是罗尔中值定理的通俗解释。

若函数满足：

在闭区间 上连续

在开区间 上可导

那么在(a,b)上一定存在至少一个点x，该点导数f'(x)=0

个人理解：函数AB两点间连线，如果线的斜率为0，或者说曲线首尾值相等，那么区间里面至少一点的斜率为0

--------------

拉格朗日中值定理：假设有一辆车，时间与当前位移的函数如下所示：

 

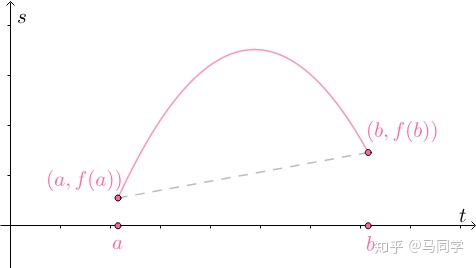
 已知首尾时间和对应位移，可以算出这段时间的平均速度为

f(b)-f(a)/(b-a)   

速度存在平均速度和瞬时速度两个概念，汽车在行驶过程时肯定是存在变速的，表现出来就是这个曲线每一时刻的切线斜率都不一样.

它应该是罗尔定理的推广版，不要求首尾两点值相等了，AB连线至少一点斜率为AB的斜率。

f(b)-f(a)=f'(x)(b-a)

--------

而柯西中值定理进一步进行推广，扩展到了两个函数上。

对于两个函数f(x)和g(x)   满足[a,b]上连续 (a,b)上可导 且任一g'(x)不等于0

至少存在一点x   使得f(b)-f(a)/g(b)-g(a) = f'(x)/g'(x)