结对编程项目-四则运算阶段性总结
结对编程项目-四则运算阶段性总结
在这段时间的结对编程过程中,我和我的组员一同编程,初步完成了项目的要求,现在我将阶段性的成果做一个总结
一、需求分析
实现一个命令行程序,要求:
- 1、自动生成小学四则运算题目(加、减、乘、除)
- 2、支持整数
- 3、支持多运算符(比如生成包含100个运算符的题目)
- 4、支持真分数
- 5、统计正确率
从题目要求可知,我们需要实现以下几个功能:
- 随机生成个四则运算题目,并可手动控制生成的题目数目
- 能将计算的结果转化为分数
- 自动计算生成题目的结果,并能判断用户输入是否与运算结果相同
现阶段已实现要求2、3,要求4虽已初步实现但仍存在一些问题,我们将会在下一阶段中实现所有项目要求的功能,并可拓展以下功能:
- 随机生成题目
- 题目去重
- 生成题目后从文件读入并判题
二、设计思路
根据需求,考虑程序需要定义方法来实现中缀表达式转后缀表达式、后缀式计算的功能,将结果转换为分数以及需要定义调用以上三种种方法并进行输入输出的主类,于是我将前两种方法放入MyDC的类中,真数的支持放入Rational类中,主类设置为MyDCTester。
1、将输入的中缀表达式转化为后缀表达式
运用老师在博客中提供的法则:
- 如果遇到数字,我们就直接将其输出。
- 如果遇到非数字时,若栈为空或者该符号为左括号或者栈顶元素为括号,直接入栈。
- 如果遇到一个右括号,持续出栈并输出符号,直到栈顶元素为左括号,然后将左括号出栈(注意,左括号只出栈,不输出),右括号不入栈。
- 如果遇到运算符号且栈非空,查看栈顶元素,如果栈顶元素的运算优先级大于或者等于该运算符号,则持续出栈,直到栈顶元素优先级小于该运算符。最后将该元素入栈。
- 如果我们读到了输入的末尾,则将栈中所有元素依次弹出。
使用if-else以及switch语句在程序中实现该规律。
在程序中我使用了字符串栈stacktwo,并定义了trans方法实现功能,代码如下:
public String trans(String before){
int i,j=0;
char step[] = before.toCharArray();//将中缀式字符串转化为字符数组
char after[] = new char[step.length];//用于接收转化后的后缀式表达式
for(i=0;i<step.length;i++) {
if (step[i] >= '0' && step[i] <= '9') {//遇到数字
after[j] = step[i];
j++;
if(i==(step.length)-1){//读到了输入的末尾
while(stacktwo.empty()==false) {
after[j]=stacktwo.pop();
j++;
}
}
}
else if(stacktwo.empty()||step[i]=='('||stacktwo.peek()=='('||stacktwo.peek()==')') {//遇到非数字且栈为空或者该符号为左括号或者栈顶元素为括号
stacktwo.push(new Character(step[i]));
if(i==(step.length)-1){
while(stacktwo.empty()==false) {
after[j]=stacktwo.pop();
j++;
}
}
}
else if(step[i]==')') {//遇到一个右括号
while (stacktwo.peek() != '(') {
after[j] = stacktwo.pop();
j++;
}
stacktwo.pop();
if(i==(step.length)-1){
while(stacktwo.empty()==false) {
after[j]=stacktwo.pop();
j++;
}
}
}
else {//遇到运算符号且栈非空
switch (step[i]) {
case ADD:
case SUBTRACT:
{
while(stacktwo.peek()=='*'||stacktwo.peek()=='/'||stacktwo.peek()=='+'||stacktwo.peek()=='-'){
after[j]=stacktwo.pop();
j++;
if(stacktwo.empty()){
break;
}
}
stacktwo.push(step[i]);
break;
}
case MULTIPLY:
case DIVIDE:
{
while(stacktwo.peek()=='*'||stacktwo.peek()=='/'){
after[j]=stacktwo.pop();
j++;
if(stacktwo.empty()){
break;
}
}
stacktwo.push(step[i]);
break;
}
}
if(i==(step.length)-1){
while(stacktwo.empty()!=false) {
after[j]=stacktwo.pop();
j++;
}
}
}
}
String str = new String(after);
return str;//将字符数组转化为字符串后返回
}
2、后缀式表达式的运算。
老师给的链接中已经明确给出了计算的方法,方法如下:
- 设置一个操作数栈,开始栈为空;
- 从左到右扫描后缀表达式,遇操作数,进栈;
- 若遇运算符,则从栈中退出两个元素,先退出的放到运算符的右边,后退出的放到运算符左边,运算后的结果再进栈,直到后缀表达式扫描完毕。
在程序中我以老师给的代码例子为基础,加以自己的理解,使用了整型栈stack,并定义了evaluate以及evalSingleOp方法来实现功能,代码如下:
public int evaluate(String expr) {//计算后缀式的值
int op1, op2, result = 0,i;
char token[]=expr.toCharArray();//将后缀式字符串转化为字符数组
for(i=0;i<token.length;i++){
if (token[i]=='+' || token[i]=='-' || token[i]=='*' || token[i]=='/') {//对每个字符进行分析,如果是运算符就取出栈顶开始的两个数
op2 = stack.pop();
op1 = stack.pop();
result = evalSingleOp(token[i], op1, op2);//将栈中取出的两个数进行运算
stack.push(new Integer(result));//将结果压栈
} else//为数字时直接进栈
stack.push(new Integer((int)(token[i]-'0')));
}
return result;//返回计算结果
}
private int evalSingleOp(char operation, int op1, int op2) {//对栈中取出的两个数进行四则运算,operation为后缀式中的运算符号
int result = 0;
switch (operation) {
case ADD:
result = op1 + op2;
break;
case SUBTRACT:
result = op1 - op2;
break;
case MULTIPLY:
result = op1 * op2;
break;
case DIVIDE:
result = op1 / op2;
}
return result;//返回运算结果
}
3、支持真分数
我们通过学习教材上第100页的例子22封装了有理数类Rational,实现了对真分数的支持。
代码如下:
public class Rational {
int numerator = 1;//分子
int denominator = 1;//分母
void setNumerator(int a) {//设置分子
int c = f(Math.abs(a), denominator);//计算最大公约数
numerator = a / c;
denominator = denominator / c;
if (numerator < 0 && denominator < 0) {
numerator = -numerator;
denominator = -denominator;
}
}
void setDenominator(int b) {//设置分母
int c = f(numerator, Math.abs(b));//计算最大公约数
numerator = numerator / c;
denominator = b / c;
if (numerator < 0 && denominator < 0) {
numerator = -numerator;
denominator = -denominator;
} else if (numerator > 0 && denominator < 0) {
numerator = -numerator;
denominator = -denominator;
}
}
int getNumerator() {
return numerator;
}
int getDenominator() {
return denominator;
}
int f(int a, int b) {//求a,b的最大公约数
if (a == 0) {
return 1;//c为分母不能为0
}
if (a < b) {//令a>b
int c = a;
a = b;
b = c;
}
int r = a % b;
while (r != 0) {
a = b;
b = r;
r = a % b;
}
return b;
}
Rational add(Rational r) {//加法运算
int a = r.getNumerator();//返回有理数r的分子
int b = r.getDenominator();//返回有理数r的分母
int newNumerator = numerator * b + denominator * a;//计算出新分子
int newDenominator = denominator * b;//计算出新分母
Rational result = new Rational();
result.setNumerator(newNumerator);
result.setDenominator(newDenominator);
return result;
}
Rational sub(Rational r) {//减法运算
int a = r.getNumerator();
int b = r.getDenominator();
int newNumerator = numerator * b - denominator * a;
int newDenominator = denominator * b;
Rational result = new Rational();
result.setNumerator(newNumerator);
result.setDenominator(newDenominator);
return result;
}
Rational muti(Rational r) {//乘法运算
int a = r.getNumerator();
int b = r.getDenominator();
int newNumerator = numerator * a;
int newDenominator = denominator * b;
Rational result = new Rational();
result.setNumerator(newNumerator);
result.setDenominator(newDenominator);
return result;
}
Rational div(Rational r) {//除法运算
int a = r.getNumerator();
int b = r.getDenominator();
Rational result = new Rational();
if (a == 0) {
System.out.println("分母不能为0");
result.setNumerator(0);
System.exit(0);
} else {
int newNumerator = numerator * b;
int newDenominator = denominator * a;
result.setNumerator(newNumerator);
result.setDenominator(newDenominator);
}
return result;
}
}
4、调用方法并实现输入输出
现阶段为减少程序调试的难度,我们使用了老师在博客中提供的代码,但老师提供的代码无法实现随机生成题目、支持真分数以及统计正确率的功能,于是我们做出了修改,使得程序可以支持分数输出,在接下来的编程中我们会根据需求对这部分代码进行重新编写。
public class MyDCTester {
public static void main(String[] args) {
String expression, again;
Rational result=new Rational();
try {
Scanner in = new Scanner(System.in);
do {
MyDC evaluator = new MyDC();
System.out.println("Enter a valid postfix expression: ");
expression = in.nextLine();//输入运算表达式
result = evaluator.evaluate(evaluator.trans(expression));//调用trans方法以及evaluate方法进行转化以及输出计算结果
System.out.println();
int a=result.getNumerator();
int b=result.getDenominator();
if (b==1){//分数转换
System.out.println("result="+a);
}
else{
System.out.println("result="+a+"/"+b);
}
System.out.print("Evaluate another expression [Y/N]? ");//询问用户是否再次计算
again = in.nextLine();
System.out.println();
}
while (again.equalsIgnoreCase("y"));
} catch (Exception IOException) {
System.out.println("Input exception reported");
}
5、UML类图
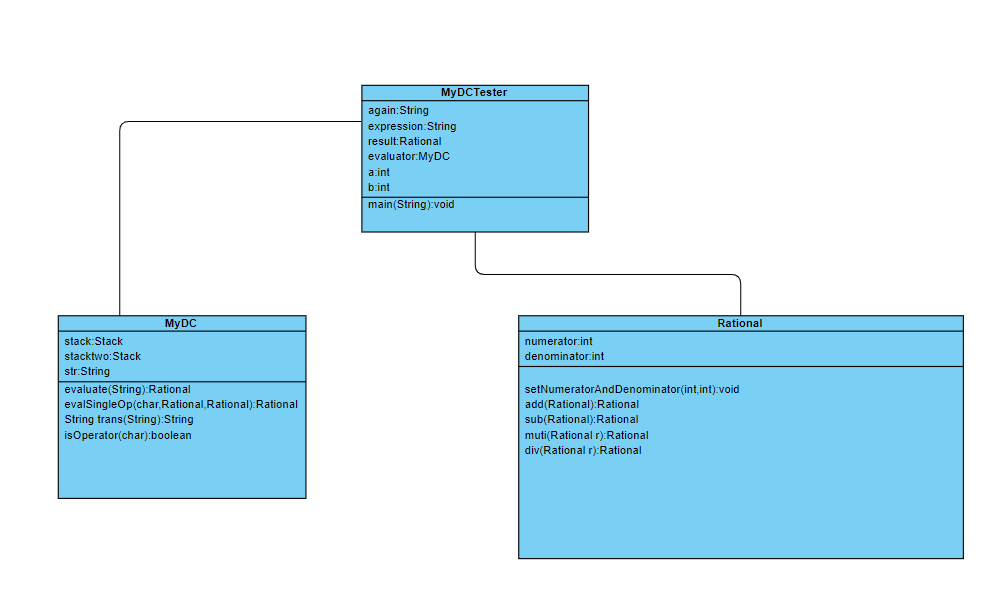
三、实现过程中的关键代码解释
我已在设计思路部分给出了设计思路并对关键代码进行了注释。
四、运行过程截图
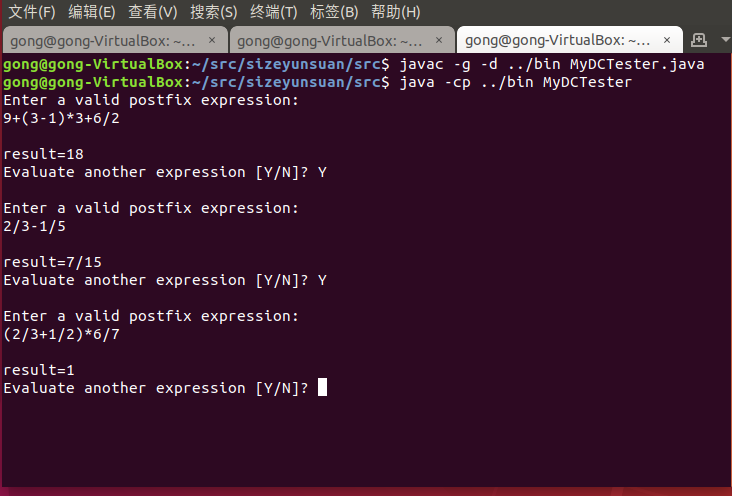
五、代码托管地址
六、遇到的困难及解决方法
到目前为止的困难主要在于实现中缀表达式转化为后缀表达式以及分数的转化,我将一些细节的问题写在了下面。
- 问题一:不知如何将字符串转化为字符数组
- 问题一解决办法:翻书时注意到书上第八章的toCharArray()方法可以实现该转化过程。
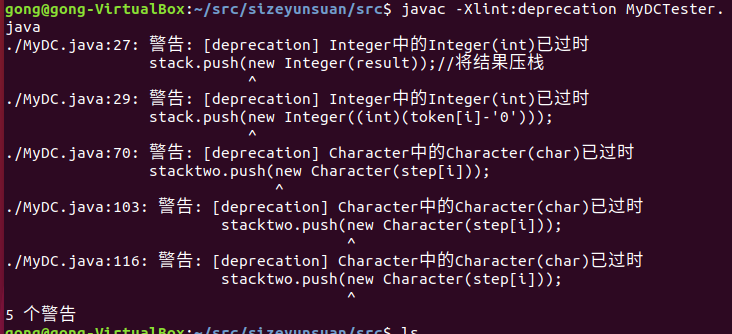
- 问题二:在命令行中编译程序时遇到如图所示的问题

- 问题二解决办法:使用
-Xlint:deprecation命令进行编译,找到问题并修改。
七、对结对的小伙伴做出评价
我的结对搭档是江野,在合作的过程中我是牵头人,他也积极响应我的号召,在编程过程中我们互相学习,在遇到困难时一起讨论解决办法。希望能在以后的任务中继续合作,也希望搭档能更加积极地参与到项目中。
八、PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 15 | 30 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 25 | 35 |
| · Design Spec | · 生成设计文档 | 30 | 30 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 20 | 30 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 35 | 45 |
| · Design | · 具体设计 | 60 | 80 |
| · Coding | · 具体编码 | 150 | 200 |
| · Code Review | · 代码复审 | 30 | 35 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 20 | 35 |
| Reporting | 报告 | 60 | 80 |
| · Size Measurement | · 计算工作量 | 10 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 20 | 20 |
| 合计 | 475 | 640 |


