复现-SHCTF2024-week4-Crypto

Crypto

复现参考文献：2024-SHCTF-week4-wp-crypto | 糖醋小鸡块的blog

鸡块师傅真的太强了（膜拜

*siDH

就讲一下这题遇到的问题，鸡块师傅说的可能不是很清楚。

这里先贴一下参考文献：

前几天源鲁杯有一题，翻到最后就是，里面有讲数据的构造，和攻击思想微信公众平台

（贴一下）

Castryck-Decru攻击

Castryck-Decru攻击是针对SIDH的一种爆破型攻击，旨在针对p比较小的椭圆曲线进行爆破攻击

攻击基于Kani的“可约性准则”，用于判断从两个椭圆曲线的乘积出发的同态是否再次回到椭圆曲线的乘积，或者到达一个二元曲线的雅可比矩阵

• 攻击首先猜测秘密同源的前几位三进制数字。
• 然后，不是逐个恢复剩余的数字，而是直接从(2,2)-同源链的结果计算秘密同源。
• 使用内射two_i和期望数据计算tauhatkernel_distort。
• 调用AuxiliaryIsogeny函数计算辅助同源和相关链。
• 使用Does22ChainSplit函数检查是否存在分裂链，这是攻击成功的关键条件。
• 计算Weil配对以恢复Bob的私钥。

项目地址：https://github.com/GiacomoPope/Castryck-Decru-SageMath

回到这题，我就当黑盒直接调用了，具体原理我也不懂

根据攻击需要的参数，我们就差a和b，我们有素数\(p=2^a*3^b-1\)，p可以在output里的EB最后拿到p的值，由于数值比较小我们可以对p加1然后去factordb查到a1和b1，a2和b2同理

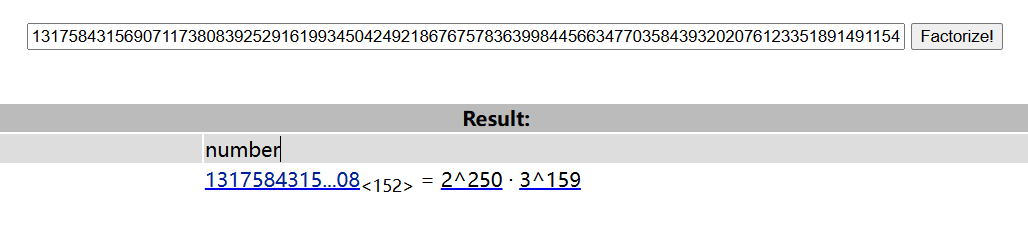
之后就是构造椭圆曲线，具体参考源鲁杯的构造方法。

（我不知道如何直接用数值构造椭圆曲线，那样运行会报错）

接下来看exp就好了，注意点就是要在项目文件夹内运行，然后求sk2时需要多加一个--sandwich(把断言去掉就好了)。

贴一下sk2的运行结果

exp

"""#!/usr/bin/env sage

from Crypto.Util.number import *
from Crypto.Cipher import AES
from hashlib import md5
from flag import flag

def gen_param(B):
 while True:
  a = randint(B >> 1, B)
  b = randint(B >> 2, B >> 1)
  p = 2**a * 3**b - 1
  if is_prime(p):
   return a, b

def gen_dmap(E):
 return E.isogeny(E.lift_x(ZZ(1)), codomain = E)

def gen_tpt(E, a, b):
 P, Q = [((p + 1) // 2**a) * _ for _ in E.gens()]
 R, S = [((p + 1) // 3**b) * _ for _ in E.gens()]
 return P, Q, R, S

def keygen(EC, b, P, Q, R, S):
 skey = randint(1, 3**b)
 T = R + skey * S
 phi = EC.isogeny(T, algorithm = "factored")
 _phi_dom, _phi_P, _phi_Q = phi.codomain(), phi(P), phi(Q)
 return skey, _phi_dom, _phi_P, _phi_Q


a1,b1 = gen_param(350)
p1 = 2**a1 * 3**b1 - 1
F1.<x> = GF(p1^2, modulus = x**2 + 1)
EC1 = EllipticCurve(F1, [0, 6, 0, 1, 0])
P1, Q1, R1, S1 = gen_tpt(EC, a1, b1)
print(f'P1={P1.xy()}')
print(f'Q1={Q1.xy()}')
print(f'R1={R1.xy()}')
print(f'S1={S1.xy()}')

sk1, _phi1_dom, _phi1_P, _phi1_Q = keygen(EC, b1, P1, Q1, R1, S1)
print(f'EC1:{_phi1_dom}')
print(f'PB1={_phi1_P.xy()}')
print(f'QB2={_phi1_Q.xy()}')

a2,b2 = gen_param(610)
p2 = 2**a2 * 3**b2 - 1
F2.<x> = GF(p2^2, modulus = x**2 + 1)
EC2 = EllipticCurve(F2, [0, 6, 0, 1, 0])
P2, Q2, R2, S2 = gen_tpt(EC, a2, b2)
print(f'P2={P2.xy()}')
print(f'Q2={Q2.xy()}')
print(f'R2={R2.xy()}')
print(f'S2={S2.xy()}')
sk2, _phi2_dom, _phi2_P, _phi2_Q = keygen(EC, b2, P2, Q2, R2, S2)
print(f'EC2:{_phi2_dom}')
print(f'PB2={_phi1_P.xy()}')
print(f'QB2={_phi1_Q.xy()}')

key = md5(long_to_bytes(sk1)).digest()
iv = md5(str(sk2).encode()).digest()

cipher = AES.new(key, AES.MODE_CFB, iv=iv)
enc = cipher.encrypt(flag)

print(f'enc = {enc.hex()}')
"""
#https://mp.weixin.qq.com/s/rzxJZT3AhJa8_y8Y0jLn6A
#https://github.com/GiacomoPope/Castryck-Decru-SageMath
"""# 求sk1

# 替换SIKEp434.sage从load后到attack前
a=250
b=159

p = 2^a*3^b - 1
public_values_aux.p = p
Fp2.<i> = GF(p^2, modulus=x^2+1)
R.<x> = PolynomialRing(Fp2)

E_start = EllipticCurve(Fp2, [0,6,0,1,0])
E_start.set_order((p+1)^2, num_checks=0) # Speeds things up in Sage

# Generation of the endomorphism 2i
two_i = generate_distortion_map(E_start)

# Generate public torsion points, for SIKE implementations
# these are fixed but to save loading in constants we can
# just generate them on the fly
P2, Q2, P3, Q3 = generate_torsion_points(E_start, a, b)
check_torsion_points(E_start, a, b, P2, Q2, P3, Q3)
A=Fp2(4189289089477997468544979453822695400500584265495091803346578638134562448932335970687326793676571649785862746844702037419185523428130990204162507604142*i+8453144899752979274082603184674998770084621842778345709593026085665609787243919407101520453085615209143595825360981888699031968367621444521989681207925)
C=Fp2(10876663327831437262436092946202594533286519870258843389665958485316202856443113411424811891669071467324995879309148604251803514827408043800152902428079*i+4101994484351838878118339435531362623951299298760741543454654959627592905764432016193446997841956209731202742983657859454109374390742351108699397540937)
EB = EllipticCurve(Fp2, [0, 6, 0, A, C])
EB.set_order((p + 1)^2, num_checks=0)

PB_x = Fp2(400743151686086340244873453949520840608574156208868642818110176396852951486095204394646889447695188912538995843668914636276137300969251924860731987594*i + 8066723303558125260716197269861828046216772084431033719257537396188532673015028142277860187197048570426361924628036485855109504692435989532466549892337)
PB_y = Fp2(7857822094787553865337300888116802881139911120764957076597259295643802343603595437056405429678918577452653990040253270552510408546662517341930347472071*i + 10256174272055348496449952390378894222811363081031264681923652307005325570743231607657784873505317820364596562401946711140198577008958311498216702686123)
PB_z = Fp2(1)

QB_x = Fp2(11265527532569587904111577151486645315441536837729457283471778056974474854267045024868622287870300007236540035625960216806930485893214503444708227243383*i + 11572347052548869297030219234396257199641564118601390459458935400217229709294039384097088201478090062341631595370187207194936531910796633969532025890187)
QB_y = Fp2(1238001162632333913423959416649793026045237600008578022715875560482397022195744581004778851687493893610142113162366180305156034033668836817430095906149*i + 9355808802624221590053977160056741459388657876928397271333623542173291286953283614788931011423156931539777202646167976404136542556319294668512474371234)
QB_z = Fp2(1)

PB = EB(PB_x, PB_y, PB_z)
QB = EB(QB_x, QB_y, QB_z)"""

"""
# 求sk2
# 同上替换数据
# 这个需要加参数进行爆破--sandwich(将内部断言去掉)
a=486
b=301

p = 2^a*3^b - 1
public_values_aux.p = p
Fp2.<i> = GF(p^2, modulus=x^2+1)
R.<x> = PolynomialRing(Fp2)

E_start = EllipticCurve(Fp2, [0,6,0,1,0])
E_start.set_order((p+1)^2, num_checks=0) # Speeds things up in Sage

# Generation of the endomorphism 2i
two_i = generate_distortion_map(E_start)

# Generate public torsion points, for SIKE implementations
# these are fixed but to save loading in constants we can
# just generate them on the fly
P2, Q2, P3, Q3 = generate_torsion_points(E_start, a, b)
check_torsion_points(E_start, a, b, P2, Q2, P3, Q3)
A=Fp2(59535702210902206632057724266122403485782121930269490904764357850731481931811358892291834226309250891450990328900036049280010419604141194291637296730727328703913164680567403783556426953678285004014585121686544887056773006148356101004676806983339649844157509652742849487058509475632164255987*i+64852232435177399443640158784531454040944394241934383260903245435876484235545723851033335774817478661385417394748201477353536461419931926490835275348734525706542632524107755972171394421922803412948624633078480838779833967459391738992623265735881364492275499237263259819337503800949666114300)
C=Fp2(61050690806389187934769383126786350986004548885068804715147802394614409167263078704960954888018441383310078678346054616498251041749628728818830924510356529523120808407048389377565446266649410216170097464816755297151018034985942268859099759375206161519933062527753348065060632492394513384086*i+8077074439258024172434168944099867368398890225954529153626574422394594541950204447361509876049948251527290252332533540126109187259353923004317852092303146292126930346834737856487032520566066787020590518347408517607586872466242304341998561230199735904938577495873392435708081679419091264767)
EB = EllipticCurve(Fp2, [0, 6, 0, A, C])
EB.set_order((p + 1)^2, num_checks=0)

PB_x = Fp2(416996386611953912381825671411217896862273056276393640633857992847371853210568257096183885552618362723081850781382485053310040111838223298831389037016745104797263137119258673015585863160793951306139520262051168484452018201607146541321879548245965120060708406056548188263109428770184470679*i + 20592158493675665198495392336832601510295492846540435551041621150757189812529173392073328659255009380759876334891966292009700608091292588069484836373960820208560629600373809653827704658519366030767296831927997226766001416180323174025471476178795433544546769173932191085724053540646639944729)
PB_y = Fp2(71934255319779473319456231037521357239577461842639834638995781561962276154205648471319881543016508220120521945006188958766711918515927736666300390531510013013219752222136876849357120821173182094753920757720079350217559660597480161836396311343966037676936442963053804573072914962152460674663*i + 79176415376881574459252426057416542844132750411766663750705407197328587941817178923562720329407116594864696212948749892818055154804078699130984677442760292980510087006005991843768472531019069389511942796903023273249068773581958501468457621161962887712050221461681839141585467402591793645894)
PB_z = Fp2(1)

QB_x = Fp2(81399207896220104838523199229123942836223942998672721447617471088799933546789833887166127001116791183009155784956302068892276943497990222792723633019021458579696541635684638373573953057978849292600240170943085361633813448722609135351165092224283296296707819206674751128093132678767574518299*i + 59565272697509141787703630456883972192553675699784211987893422193583642170431575906952477269198392298815160807657217599332116732898901549042831683061911999197598082798698793498902676161570298508553574866686598052406458954435987817164049241700002339342165193999242704894297418052166335638731)
QB_y = Fp2(21930351134214703951291759959503306221382335091685056420498342039206078305903361133512863350368812584471061688170029056369164678056492881926814997907481142982389978084439411052754236340914978327950474951824251797939798502875399920157660381059113442352137267881283959649753286318015289023163*i + 32177434323242823799795301005877693615760991886819458542076959058162762244773500905362804118528323187241784967539643917408903962138638896033673432863920521413676017199387780524917678271106039934571641676244524711655457465408480508716026824510901729812960266245895067755449573368867399411326)
QB_z = Fp2(1)

PB = EB(PB_x, PB_y)
QB = EB(QB_x, QB_y, QB_z)

"""

from Crypto.Util.number import *
from Crypto.Cipher import AES
from hashlib import md5
sk1=3599349351989826939257244168875987905412334469321466246296914822246846713144
sk2=265224889924040230352809890018188742288829460808797625767564487574491813646343173069577492003667305149036083853277964262066159526193356944364624
enc = "2ba4fd55c06bfcc9d253d3a60ec1eaaa82d482ff671d088b4f1354ebad2400d54a3bdd1dd1e38bf25a334f5fd3ec98ea89"
enc=bytes.fromhex(enc)
key = md5(long_to_bytes(sk1)).digest()
iv = md5(str(sk2).encode()).digest()

cipher = AES.new(key, AES.MODE_CFB, iv=iv)
enc = cipher.decrypt(enc)
print(enc)


"""
#这里放一下求sk2的例子
#需要放在那个项目文件夹下运行(即可直接覆盖SIKEp434.sage)

import public_values_aux
from public_values_aux import *

load('castryck_decru_shortcut.sage')
load('sandwich_attack.sage')

a=486
b=301

p = 2^a*3^b - 1
public_values_aux.p = p
Fp2.<i> = GF(p^2, modulus=x^2+1)
R.<x> = PolynomialRing(Fp2)

E_start = EllipticCurve(Fp2, [0,6,0,1,0])
E_start.set_order((p+1)^2, num_checks=0) # Speeds things up in Sage

# Generation of the endomorphism 2i
two_i = generate_distortion_map(E_start)

# Generate public torsion points, for SIKE implementations
# these are fixed but to save loading in constants we can
# just generate them on the fly
P2, Q2, P3, Q3 = generate_torsion_points(E_start, a, b)
check_torsion_points(E_start, a, b, P2, Q2, P3, Q3)
A=Fp2(59535702210902206632057724266122403485782121930269490904764357850731481931811358892291834226309250891450990328900036049280010419604141194291637296730727328703913164680567403783556426953678285004014585121686544887056773006148356101004676806983339649844157509652742849487058509475632164255987*i+64852232435177399443640158784531454040944394241934383260903245435876484235545723851033335774817478661385417394748201477353536461419931926490835275348734525706542632524107755972171394421922803412948624633078480838779833967459391738992623265735881364492275499237263259819337503800949666114300)
C=Fp2(61050690806389187934769383126786350986004548885068804715147802394614409167263078704960954888018441383310078678346054616498251041749628728818830924510356529523120808407048389377565446266649410216170097464816755297151018034985942268859099759375206161519933062527753348065060632492394513384086*i+8077074439258024172434168944099867368398890225954529153626574422394594541950204447361509876049948251527290252332533540126109187259353923004317852092303146292126930346834737856487032520566066787020590518347408517607586872466242304341998561230199735904938577495873392435708081679419091264767)
EB = EllipticCurve(Fp2, [0, 6, 0, A, C])
EB.set_order((p + 1)^2, num_checks=0)

PB_x = Fp2(416996386611953912381825671411217896862273056276393640633857992847371853210568257096183885552618362723081850781382485053310040111838223298831389037016745104797263137119258673015585863160793951306139520262051168484452018201607146541321879548245965120060708406056548188263109428770184470679*i + 20592158493675665198495392336832601510295492846540435551041621150757189812529173392073328659255009380759876334891966292009700608091292588069484836373960820208560629600373809653827704658519366030767296831927997226766001416180323174025471476178795433544546769173932191085724053540646639944729)
PB_y = Fp2(71934255319779473319456231037521357239577461842639834638995781561962276154205648471319881543016508220120521945006188958766711918515927736666300390531510013013219752222136876849357120821173182094753920757720079350217559660597480161836396311343966037676936442963053804573072914962152460674663*i + 79176415376881574459252426057416542844132750411766663750705407197328587941817178923562720329407116594864696212948749892818055154804078699130984677442760292980510087006005991843768472531019069389511942796903023273249068773581958501468457621161962887712050221461681839141585467402591793645894)
PB_z = Fp2(1)

QB_x = Fp2(81399207896220104838523199229123942836223942998672721447617471088799933546789833887166127001116791183009155784956302068892276943497990222792723633019021458579696541635684638373573953057978849292600240170943085361633813448722609135351165092224283296296707819206674751128093132678767574518299*i + 59565272697509141787703630456883972192553675699784211987893422193583642170431575906952477269198392298815160807657217599332116732898901549042831683061911999197598082798698793498902676161570298508553574866686598052406458954435987817164049241700002339342165193999242704894297418052166335638731)
QB_y = Fp2(21930351134214703951291759959503306221382335091685056420498342039206078305903361133512863350368812584471061688170029056369164678056492881926814997907481142982389978084439411052754236340914978327950474951824251797939798502875399920157660381059113442352137267881283959649753286318015289023163*i + 32177434323242823799795301005877693615760991886819458542076959058162762244773500905362804118528323187241784967539643917408903962138638896033673432863920521413676017199387780524917678271106039934571641676244524711655457465408480508716026824510901729812960266245895067755449573368867399411326)
QB_z = Fp2(1)

PB = EB(PB_x, PB_y)
QB = EB(QB_x, QB_y, QB_z)
# ===================================
# =====  ATTACK  ====================
# ===================================

def RunAttack(num_cores):
    return CastryckDecruAttack(E_start, P2, Q2, EB, PB, QB, two_i, num_cores=num_cores)

if __name__ == '__main__' and '__file__' in globals():
    if '--parallel' in sys.argv:
        # Set number of cores for parallel computation
        num_cores = os.cpu_count()
        print(f"Performing the attack in parallel using {num_cores} cores")
    else:
        num_cores = 1

    if '--sandwich' in sys.argv:
        recovered_key = SandwichAttack(E_start, P2, Q2, EB, PB, QB, two_i, k=5, alp=0)
    else:
        recovered_key = RunAttack(num_cores)


"""