网鼎杯2024-青龙官方资格赛
没必要看,只有最简单的题
哎,尽力了,简单的都做不出来
Crypto
crypto1
from Crypto.Util.number import *
from secret import flag
p = getPrime(512)
q = getPrime(512)
n = p * q
d = getPrime(299)
e = inverse(d,(p-1)*(q-1))
m = bytes_to_long(flag)
c = pow(m,e,n)
hint1 = p >> (512-70)
hint2 = q >> (512-70)
print(f"n = {n}")
print(f"e = {e}")
print(f"c = {c}")
print(f"hint1 = {hint1}")
print(f"hint2 = {hint2}")
参考1.3.3:2024-高校密码挑战赛赛题一-wp-crypto | 糖醋小鸡块的blog
boneh_durfee用的是别的模板,这题已经给了p和q的高位,就不需要我们爆破p和q的MSB了,直接修改example函数里的pM,s,delta这三个参数就好了,然后就是漫长的等待环节。
from Crypto.Util.number import *
from __future__ import print_function
import time
############################################
# Config
##########################################
"""
Setting debug to true will display more informations
about the lattice, the bounds, the vectors...
"""
debug = True
"""
Setting strict to true will stop the algorithm (and
return (-1, -1)) if we don't have a correct
upperbound on the determinant. Note that this
doesn't necesseraly mean that no solutions
will be found since the theoretical upperbound is
usualy far away from actual results. That is why
you should probably use `strict = False`
"""
strict = False
"""
This is experimental, but has provided remarkable results
so far. It tries to reduce the lattice as much as it can
while keeping its efficiency. I see no reason not to use
this option, but if things don't work, you should try
disabling it
"""
helpful_only = True
dimension_min = 7 # stop removing if lattice reaches that dimension
############################################
# Functions
##########################################
# display stats on helpful vectors
def helpful_vectors(BB, modulus):
nothelpful = 0
for ii in range(BB.dimensions()[0]):
if BB[ii,ii] >= modulus:
nothelpful += 1
print(nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")
# display matrix picture with 0 and X
def matrix_overview(BB, bound):
for ii in range(BB.dimensions()[0]):
a = ('%02d ' % ii)
for jj in range(BB.dimensions()[1]):
a += '0' if BB[ii,jj] == 0 else 'X'
if BB.dimensions()[0] < 60:
a += ' '
if BB[ii, ii] >= bound:
a += '~'
print(a)
# tries to remove unhelpful vectors
# we start at current = n-1 (last vector)
def remove_unhelpful(BB, monomials, bound, current):
# end of our recursive function
if current == -1 or BB.dimensions()[0] <= dimension_min:
return BB
# we start by checking from the end
for ii in range(current, -1, -1):
# if it is unhelpful:
if BB[ii, ii] >= bound:
affected_vectors = 0
affected_vector_index = 0
# let's check if it affects other vectors
for jj in range(ii + 1, BB.dimensions()[0]):
# if another vector is affected:
# we increase the count
if BB[jj, ii] != 0:
affected_vectors += 1
affected_vector_index = jj
# level:0
# if no other vectors end up affected
# we remove it
if affected_vectors == 0:
print("* removing unhelpful vector", ii)
BB = BB.delete_columns([ii])
BB = BB.delete_rows([ii])
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii-1)
return BB
# level:1
# if just one was affected we check
# if it is affecting someone else
elif affected_vectors == 1:
affected_deeper = True
for kk in range(affected_vector_index + 1, BB.dimensions()[0]):
# if it is affecting even one vector
# we give up on this one
if BB[kk, affected_vector_index] != 0:
affected_deeper = False
# remove both it if no other vector was affected and
# this helpful vector is not helpful enough
# compared to our unhelpful one
if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(bound - BB[ii, ii]):
print("* removing unhelpful vectors", ii, "and", affected_vector_index)
BB = BB.delete_columns([affected_vector_index, ii])
BB = BB.delete_rows([affected_vector_index, ii])
monomials.pop(affected_vector_index)
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii-1)
return BB
# nothing happened
return BB
"""
Returns:
* 0,0 if it fails
* -1,-1 if `strict=true`, and determinant doesn't bound
* x0,y0 the solutions of `pol`
"""
def boneh_durfee(pol, modulus, mm, tt, XX, YY):
"""
Boneh and Durfee revisited by Herrmann and May
finds a solution if:
* d < N^delta
* |x| < e^delta
* |y| < e^0.5
whenever delta < 1 - sqrt(2)/2 ~ 0.292
"""
# substitution (Herrman and May)
PR.<u, x, y> = PolynomialRing(ZZ)
Q = PR.quotient(x*y + 1 - u) # u = xy + 1
polZ = Q(pol).lift()
UU = XX*YY + 1
# x-shifts
gg = []
for kk in range(mm + 1):
for ii in range(mm - kk + 1):
xshift = x^ii * modulus^(mm - kk) * polZ(u, x, y)^kk
gg.append(xshift)
gg.sort()
# x-shifts list of monomials
monomials = []
for polynomial in gg:
for monomial in polynomial.monomials():
if monomial not in monomials:
monomials.append(monomial)
monomials.sort()
# y-shifts (selected by Herrman and May)
for jj in range(1, tt + 1):
for kk in range(floor(mm/tt) * jj, mm + 1):
yshift = y^jj * polZ(u, x, y)^kk * modulus^(mm - kk)
yshift = Q(yshift).lift()
gg.append(yshift) # substitution
# y-shifts list of monomials
for jj in range(1, tt + 1):
for kk in range(floor(mm/tt) * jj, mm + 1):
monomials.append(u^kk * y^jj)
# construct lattice B
nn = len(monomials)
BB = Matrix(ZZ, nn)
for ii in range(nn):
BB[ii, 0] = gg[ii](0, 0, 0)
for jj in range(1, ii + 1):
if monomials[jj] in gg[ii].monomials():
BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU,XX,YY)
# Prototype to reduce the lattice
if helpful_only:
# automatically remove
BB = remove_unhelpful(BB, monomials, modulus^mm, nn-1)
# reset dimension
nn = BB.dimensions()[0]
if nn == 0:
print("failure")
return 0,0
# check if vectors are helpful
if debug:
helpful_vectors(BB, modulus^mm)
# check if determinant is correctly bounded
det = BB.det()
bound = modulus^(mm*nn)
if det >= bound:
print("We do not have det < bound. Solutions might not be found.")
print("Try with highers m and t.")
if debug:
diff = (log(det) - log(bound)) / log(2)
print("size det(L) - size e^(m*n) = ", floor(diff))
if strict:
return -1, -1
else:
print("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")
# display the lattice basis
if debug:
matrix_overview(BB, modulus^mm)
# LLL
if debug:
print("optimizing basis of the lattice via LLL, this can take a long time")
BB = BB.LLL()
if debug:
print("LLL is done!")
# transform vector i & j -> polynomials 1 & 2
if debug:
print("looking for independent vectors in the lattice")
found_polynomials = False
for pol1_idx in range(nn - 1):
for pol2_idx in range(pol1_idx + 1, nn):
# for i and j, create the two polynomials
PR.<w,z> = PolynomialRing(ZZ)
pol1 = pol2 = 0
for jj in range(nn):
pol1 += monomials[jj](w*z+1,w,z) * BB[pol1_idx, jj] / monomials[jj](UU,XX,YY)
pol2 += monomials[jj](w*z+1,w,z) * BB[pol2_idx, jj] / monomials[jj](UU,XX,YY)
# resultant
PR.<q> = PolynomialRing(ZZ)
rr = pol1.resultant(pol2)
# are these good polynomials?
if rr.is_zero() or rr.monomials() == [1]:
continue
else:
print("found them, using vectors", pol1_idx, "and", pol2_idx)
found_polynomials = True
break
if found_polynomials:
break
if not found_polynomials:
print("no independant vectors could be found. This should very rarely happen...")
return 0, 0
rr = rr(q, q)
# solutions
soly = rr.roots()
if len(soly) == 0:
print("Your prediction (delta) is too small")
return 0, 0
soly = soly[0][0]
ss = pol1(q, soly)
solx = ss.roots()[0][0]
return solx, soly
def example():
t1 = time.time()
N = 104769059324906604819374246969389472089736482039584780304698351288134425847574721209477631552050746222528061242850563906415558000954816414452571907898376586538455570846715727736834959625908944488834642926192746728574287181536549647851644625185864257557629579686099455733892320222578364826099212655146530976379
e = 12337109880409970018293646110440488264982341274846829641219533345965373708872641944832903882339212178067485766669515688243675673212167726028183775964215646348775048640061665951311218967384639999950950042290221189659835294938061099700246737365693200129282703765155456889082133763568539014092220899267025682857
c = 31744736423783628269884009616541129531740686983212218114995065554639252322714403985771782435353721009653250709135160293375136413735234647281736871541268953447552855923299477737849706638177219571453513142214997506075291749228813720600113175989090030091204440975462838480365583907951185017109681679559591532826
hint1 = 864467081468962738290
hint2 = 939654974954806345061
#phih=(n-hint1-hint2+1)%(2^(512-70))
#dh=inverse_mod(e%(2^(512-70)),phih)
pM=hint1
size=512 #The size of p; size=1024 in Tables 10
length_N = 2*size
s=70; #s is the number of MSBs exhaustion, which can be chosen as we need.
nw=3 #2^nw windows
delta = 0.229
# The parameters (N, e) can be chosen as we need.
m = 12 # 格大小(越大越好/越慢)
#guess=100
# you need to be a lattice master to tweak these
t = round(((1-2*delta) * m)) # 来自 Herrmann 和 May 的优化
X = floor(N^delta) #
Y = 2*floor(N^(1/2)/2^s) # 如果 p、 q 大小相同,则正确
p0=pM*2^(size-s)+2^(size-s-1);
q0=N/p0;
qM=int(q0/2^(size-s))
A = N + 1-pM*2^(size-s)-qM*2^(size-s);
P.<x,y> = PolynomialRing(ZZ)
pol = 1 + x * (A + y) #构建的方程
if debug:
##print ("=== running algorithm ===")
start_time = time.time()
solx, soly = boneh_durfee(pol, e, m, t, X, Y)
if solx > 0:
#print ("=== solution found ===")
if False:
print ("x:", solx)
print ("y:", soly)
d_sol = int(pol(solx, soly) / e)
#print ("私钥d:", d)
#if(d_sol==d):
print ("=== solution found ===")
print ("p的高比特为:",pM)
print ("q的高比特为:",qM)
#print("p的真实高比特:",int(p/2^(512-s)))
#print("q的真实高比特:",int(q/2^(512-s)))
print ("d=",d_sol)
t2 = time.time()
print(t2-t1)
if 0:
example()
"""
=== solution found ===
p的高比特为: 864467081468962738290
q的高比特为: 939654974954806345061
d= 739638974439475993531255172202354119076210219461888654018566065491412925302888252209575273
2523.213582754135
"""
d= 739638974439475993531255172202354119076210219461888654018566065491412925302888252209575273
N = 104769059324906604819374246969389472089736482039584780304698351288134425847574721209477631552050746222528061242850563906415558000954816414452571907898376586538455570846715727736834959625908944488834642926192746728574287181536549647851644625185864257557629579686099455733892320222578364826099212655146530976379
c = 31744736423783628269884009616541129531740686983212218114995065554639252322714403985771782435353721009653250709135160293375136413735234647281736871541268953447552855923299477737849706638177219571453513142214997506075291749228813720600113175989090030091204440975462838480365583907951185017109681679559591532826
print(long_to_bytes(int(pow(c,d,N))))
#b'wdflag{c8546072-924f-46b6-a548-1a21bf67bcfc}'
crypto2
# coding: utf-8
#!/usr/bin/env python2
import gmpy2
import random
import binascii
from hashlib import sha256
from sympy import nextprime
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.number import long_to_bytes
from FLAG import flag
#flag = 'wdflag{123}'
def victory_encrypt(plaintext, key):
key = key.upper()
key_length = len(key)
plaintext = plaintext.upper()
ciphertext = ''
for i, char in enumerate(plaintext):
if char.isalpha():
shift = ord(key[i % key_length]) - ord('A')
encrypted_char = chr((ord(char) - ord('A') + shift) % 26 + ord('A'))
ciphertext += encrypted_char
else:
ciphertext += char
return ciphertext
victory_key = "WANGDINGCUP"
victory_encrypted_flag = victory_encrypt(flag, victory_key)
p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
a = 0
b = 7
xG = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
yG = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
G = (xG, yG)
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
h = 1
zero = (0,0)
dA = nextprime(random.randint(0, n))
if dA > n:
print("warning!!")
def addition(t1, t2):
if t1 == zero:
return t2
if t2 == zero:
return t2
(m1, n1) = t1
(m2, n2) = t2
if m1 == m2:
if n1 == 0 or n1 != n2:
return zero
else:
k = (3 * m1 * m1 + a) % p * gmpy2.invert(2 * n1 , p) % p
else:
k = (n2 - n1 + p) % p * gmpy2.invert((m2 - m1 + p) % p, p) % p
m3 = (k * k % p - m1 - m2 + p * 2) % p
n3 = (k * (m1 - m3) % p - n1 + p) % p
return (int(m3),int(n3))
def multiplication(x, k):
ans = zero
t = 1
while(t <= k):
if (k &t )>0:
ans = addition(ans, x)
x = addition(x, x)
t <<= 1
return ans
def getrs(z, k):
(xp, yp) = P
r = xp
s = (z + r * dA % n) % n * gmpy2.invert(k, n) % n
return r,s
z1 = random.randint(0, p)
z2 = random.randint(0, p)
k = random.randint(0, n)
P = multiplication(G, k)
hA = multiplication(G, dA)
r1, s1 = getrs(z1, k)
r2, s2 = getrs(z2, k)
print("r1 = {}".format(r1))
print("r2 = {}".format(r2))
print("s1 = {}".format(s1))
print("s2 = {}".format(s2))
print("z1 = {}".format(z1))
print("z2 = {}".format(z2))
key = sha256(long_to_bytes(dA)).digest()
cipher = AES.new(key, AES.MODE_CBC)
iv = cipher.iv
encrypted_flag = cipher.encrypt(pad(victory_encrypted_flag.encode(), AES.block_size))
encrypted_flag_hex = binascii.hexlify(iv + encrypted_flag).decode('utf-8')
print("Encrypted flag (AES in CBC mode, hex):", encrypted_flag_hex)
# output
# r1 = 86806104739558095745988469033305523200538774705708894815836887970976487278764
# r2 = 86806104739558095745988469033305523200538774705708894815836887970976487278764
# s1 = 93400851884262731807098055393482657423555590196362184363643455285862566867372
# s2 = 58741027521216057788923508334695668250013849866589902683641825341545919891746
# z1 = 47591695289461307212638536234394543297527537576682980326526736956079807805586
# z2 = 97911075901954715147720917205165523174582665086645698292621371632896283314804
# ('Encrypted flag (AES in CBC mode, hex):', u'86cd24e2914c0c4d9b87bea34005a98bd8587d14cae71909b917679d3328304e7915e6ba4cad1096faa4a85bc52f8056d3f21ef09516be8a5160f1b338a6b936')
\[s_1=(z_1+r_1*d)*k^{-1}\mod n\\
s_2=(z_2+r_2*d)*k^{-1}\mod n\\
s_1*k=z_1+r_1*d\mod n\\
s_2*k=z_2+r_2*d\mod n\\
r_1==r_2==P_x\\
两式相减得(s_1-s_2)*k=(z_1-z_2)\mod n\\
k=(z_1-z_2)*(s_1-s_2)^{-1}\mod n\\
d=(s_1*k-z_1)*z_1^{-1}\mod n
之后直接AES解密,然后移位回去就好了
\]
from hashlib import sha256
from Crypto.Cipher import AES
from Crypto.Util.number import *
from Crypto.Util.Padding import unpad
p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
a = 0
b = 7
xG = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
yG = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
G = (xG, yG)
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
r1 = 86806104739558095745988469033305523200538774705708894815836887970976487278764
r2 = 86806104739558095745988469033305523200538774705708894815836887970976487278764
s1 = 93400851884262731807098055393482657423555590196362184363643455285862566867372
s2 = 58741027521216057788923508334695668250013849866589902683641825341545919891746
z1 = 47591695289461307212638536234394543297527537576682980326526736956079807805586
z2 = 97911075901954715147720917205165523174582665086645698292621371632896283314804
E = EllipticCurve(GF(p), [a, b])
G=E(G)
Px=r1
P = E.lift_x(Px)
s=(s1-s2)%n
z=(z1-z2)%n
k=inverse_mod(s,n)*z%n
assert k*G==P
dA=(s1*k-z1)*inverse_mod(r1,n)%n
c="86cd24e2914c0c4d9b87bea34005a98bd8587d14cae71909b917679d3328304e7915e6ba4cad1096faa4a85bc52f8056d3f21ef09516be8a5160f1b338a6b936"
c=bytes.fromhex(c)
iv=c[:16]
c=c[16:]
key = sha256(long_to_bytes(int(dA))).digest()
cipher = AES.new(key, AES.MODE_CBC,iv)
m=unpad(cipher.decrypt(c),AES.block_size)
def victory_decrypt(plaintext, key):
key = key.upper()
key_length = len(key)
plaintext = plaintext.upper()
ciphertext = ''
for i, char in enumerate(plaintext):
if char.isalpha():
shift = ord(key[i % key_length]) - ord('A')
decrypted_char = chr((ord(char) - ord('A') - shift) % 26 + ord('A'))
ciphertext += decrypted_char
else:
ciphertext += char
return ciphertext.lower()
victory_key = "WANGDINGCUP"
print(victory_decrypt(m.decode(),victory_key))
#wdflag{8e4966caba96f59430cb235dbfb341e1}
Reverse
reverse1
直接看lib里面的.so文件
通过搜索关键词0xA3B1BAC6,发现是SM4加密
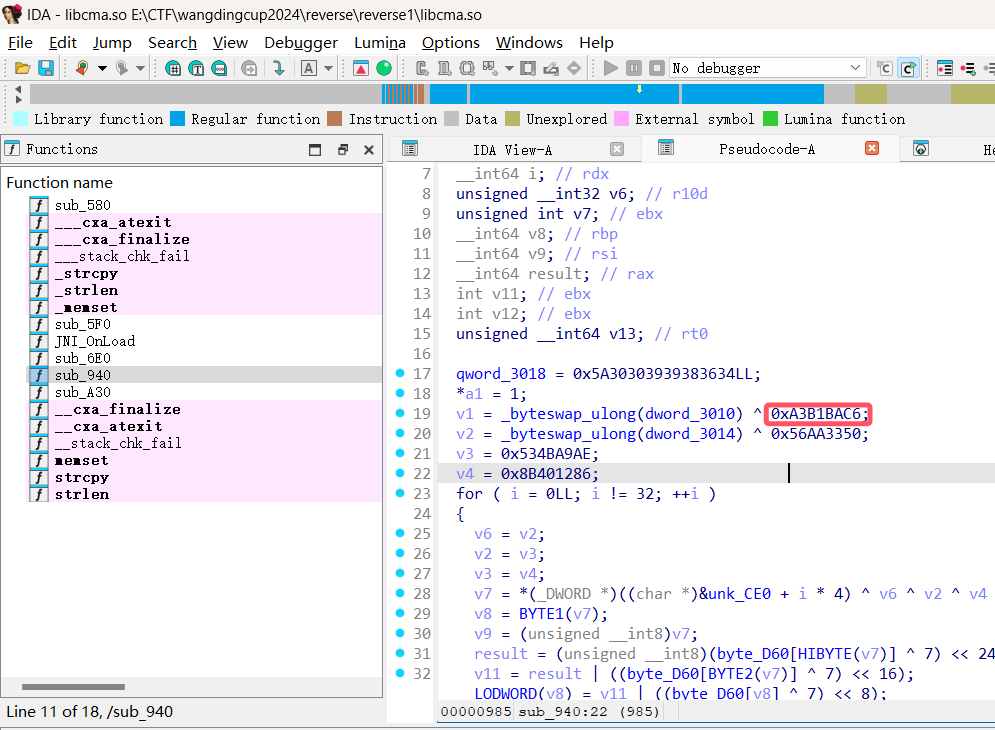
这是对密钥的异或的操作
接下来就是找密钥的环节
通过对v3,v4直接异或上fk后两位可以得到上面qword_3018的结果,所以这就是密钥的后半部分。
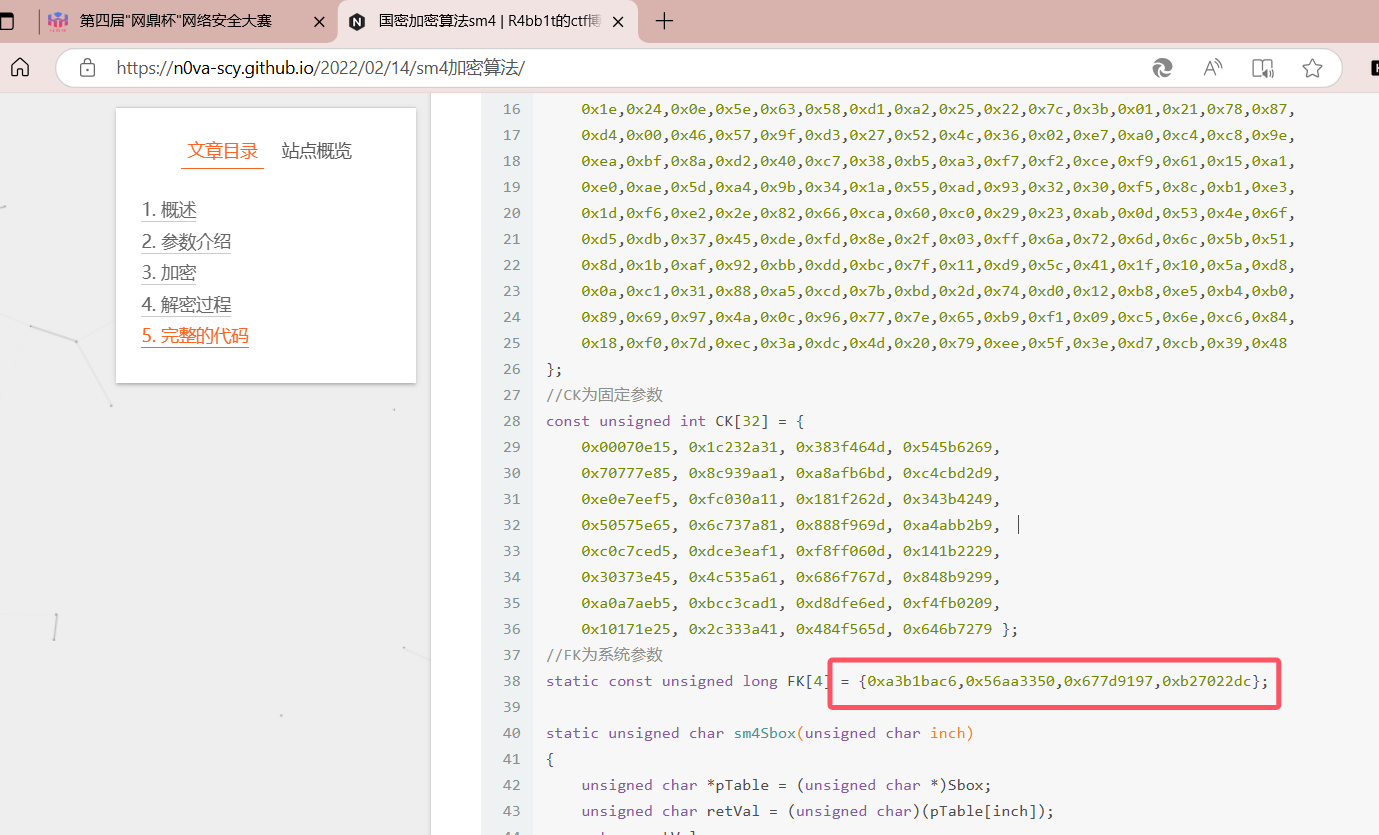
fk=[0xa3b1bac6,0x56aa3350,0x677d9197,0xb27022dc]
k3=0x534BA9AE
k4=0x8B401286
print(hex(k3^fk[2]))
print(hex(k4^fk[3]))
#0x34363839
#0x3930305a
接下来显而易见,密钥的前半部分就是dword_3010和dword_3014
可以直接查看到。
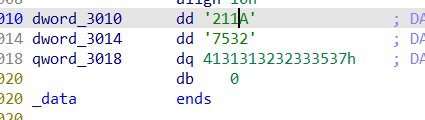
直接用cyberchef解密就好了
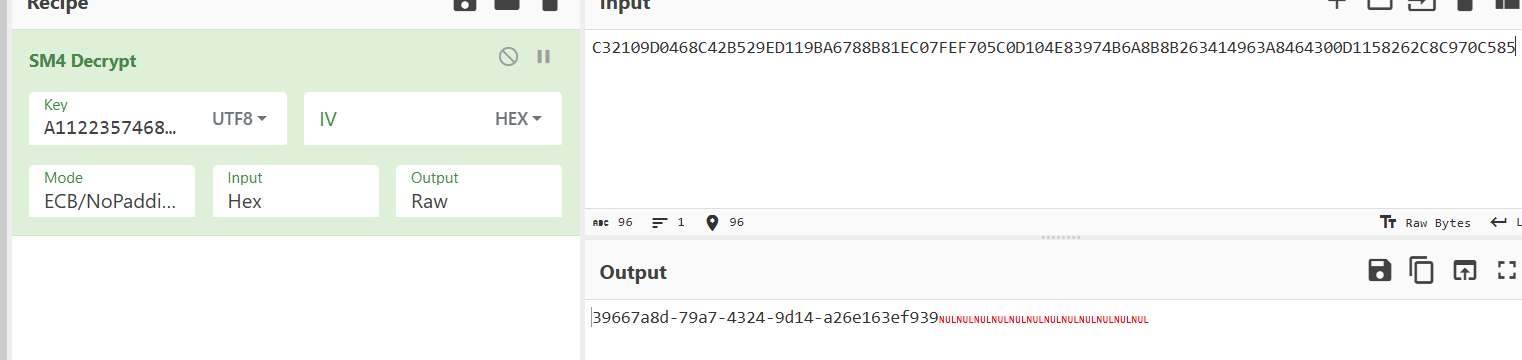
reverse2
将flag拆成了四份,都是很简单的逻辑,提取十六进制数据的时候看汇编比较好
1.无法对2求逆元,直接逐字节爆破
2.异或逆运算回去就好了
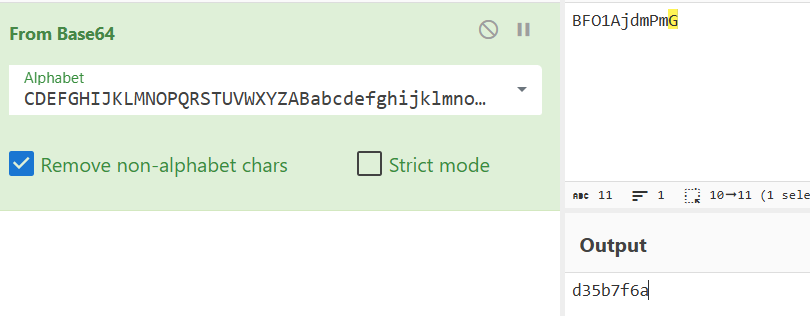
3.换表base64,程序里的表我看的时候没有C,就照过滤填在最前面就可以出了
4.AES,给了key直接解密就好了
from base64 import *
s2=[0x6a,0xc4,0xcc,0x62,0xc2,0x6e,0xca,0xca]
x=''
for i in s2:
for j in range(256):
if j*2==i:
x+=chr(j)
break
v22='XorrLord'
v11=[0x60,0x58,0x16,0x47,0x7d,0x5c,0x44,0x5d]
for i in range(len(v11)):
x+=chr(v11[i]^ord(v22[i]))
#看图1
x+='d35b7f6a'
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
c=b'\x0f\xe3\x2f\xe6\x58\x20\x9b\x3a\xd6\xe4\x18\x3f\xa7\x78\xa5\x82'
key=b'AesMasterAesMast'
cipher=AES.new(key,AES.MODE_ECB)
m=unpad(cipher.decrypt(c),AES.block_size)
x+=m.decode()
print("wdflag{"+x+"}")
Misc
misc3
将http中所有文件提取出来,发现hacker.php木马
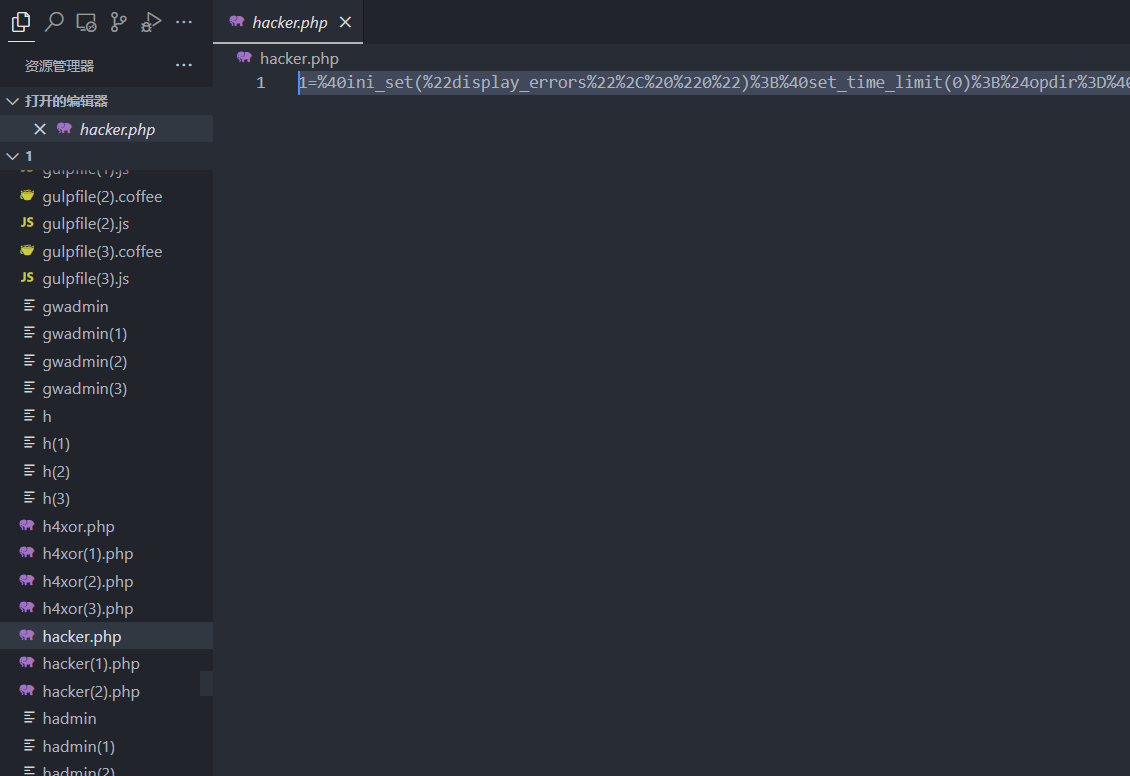
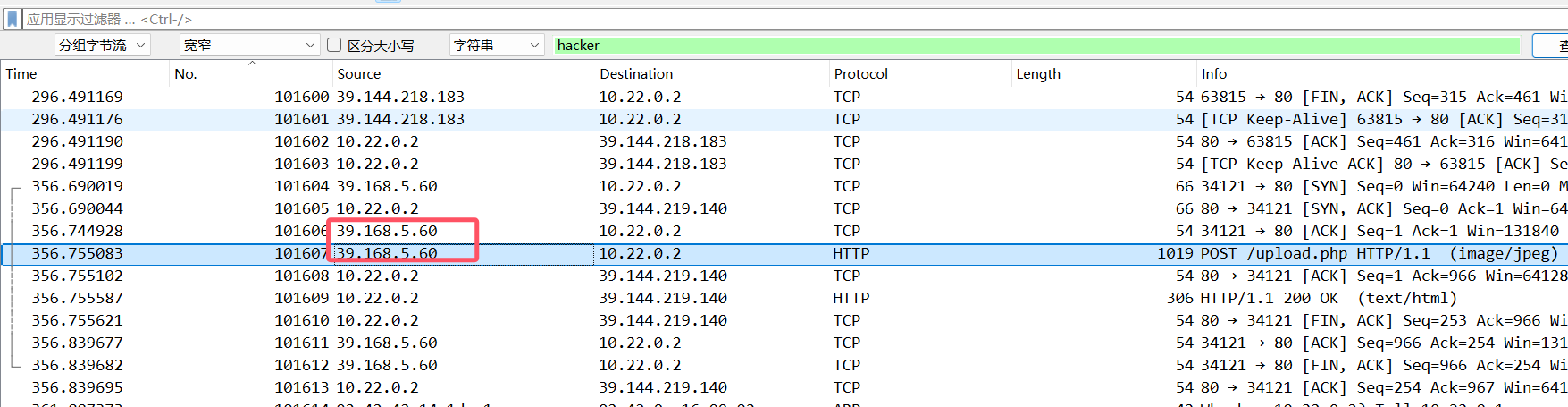
回到wireshark里搜hacker就有了


 浙公网安备 33010602011771号
浙公网安备 33010602011771号