0xGame2024-week1-crypto

Crypto

Caesar Cipher

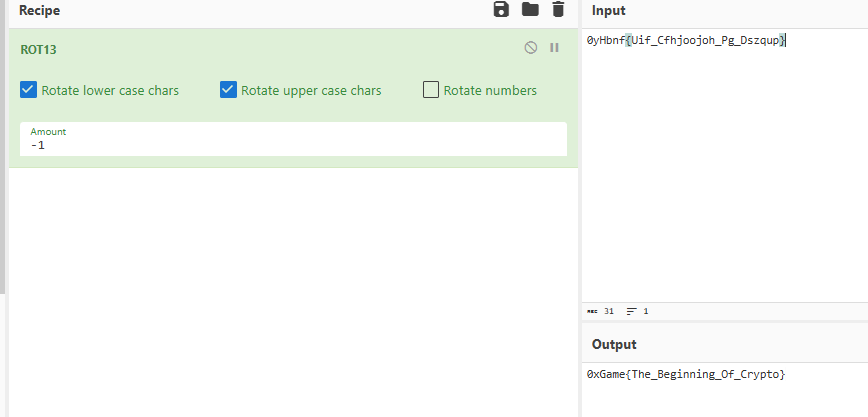
密文：0yHbnf{Uif_Cfhjoojoh_Pg_Dszqup}

提示：凯撒加密。

改成-1就好了

RSA_Easy

from Crypto.Util.number import bytes_to_long, getPrime
from hashlib import md5
from random import randint
from gmpy2 import invert,gcd

#Hash Functi
on:
def MD5(m):return md5(str(m).encode()).hexdigest()

#RSA AlgorithmParameter Generation Function:
def KeyGen():
	Factor_BitLength = 30
	q = getPrime(Factor_BitLength)
	p = getPrime(Factor_BitLength)
	N = p * q
	#Euler's totient function:
	phi = (p-1) * (q-1)

	#Generate Keys:
	while True:
		e = randint(1,phi)
		if gcd(e,phi) == 1:
			break

	#Generate Result:
	Pub_Key = (N,e)
	return Pub_Key

Pub = KeyGen()

N = Pub[0]
e = Pub[1]

#RSA Encrypt:
m = randint(1,N)
c = pow(m,e,N)

print(f'Pub_Key = {Pub}')
print(f'Encrypt_msg = {c}')

直接网站分解就行了

from Crypto.Util.number import *
from hashlib import md5

def MD5(m):return md5(str(m).encode()).hexdigest()

Pub_Key = (689802261604270193, 620245111658678815)
Encrypt_msg = 289281498571087475

# factordb
p=823642439
q=837502087
m=pow(Encrypt_msg,inverse(Pub_Key[1],(p-1)*(q-1)),p*q)

flag = '0xGame{'+ MD5(m) +'}'
print(flag)
# 0xGame{5aa4603855d01ffdc5dcf92e0e604f31}

RSA-Baby

from Crypto.Util.number import bytes_to_long, getPrime
from hashlib import md5
from random import randint
from gmpy2 import invert,gcd

#Hash Function:
def MD5(m):return md5(str(m).encode()).hexdigest()

#RSA AlgorithmParameter Generation Function:
def KeyGen():
	Factor_BitLength = 30
	q = getPrime(Factor_BitLength)
	p = getPrime(Factor_BitLength)
	N = p * q
	#Euler's totient function:
	phi = (p-1) * (q-1)

	#Generate Keys:
	while True:
		e = randint(1,phi)
		if gcd(e,phi) == 1:
			d = int(invert(e,phi))
			break

	#Generate Result:
	Pub_Key = (N,e)
	Prv_Key = (N,d)
	return Pub_Key,Prv_Key

Pub,Prv = KeyGen()

N = Pub[0]
e = Pub[1]
d = Prv[1]

#RSA Encrypt:
m = randint(1,N)
c = pow(m,e,N)

print(f'Pub_Key = {Pub}')
print(f'Prv_Key = {Prv}')
print(f'Encrypt_msg = {c}')

给了私钥直接用就好了

from Crypto.Util.number import bytes_to_long, getPrime
from hashlib import md5

def MD5(m):return md5(str(m).encode()).hexdigest()


Pub_Key = (547938466798424179, 80644065229241095)
Prv_Key = (547938466798424179, 488474228706714247)
Encrypt_msg = 344136655393256706

m=pow(Encrypt_msg,Prv_Key[1],Pub_Key[0])

flag = '0xGame{'+ MD5(m) +'}'
print(flag)

Code

"""#How to use mathematics to represent information?
from Crypto.Util.number import bytes_to_long
from base64 import b64encode
from secret import flag

msg = flag.encode()
length = len(msg)

assert length%4 == 0
block = length//4
m = [ msg[ block*(i) : block*(i+1) ] for i in range(4) ]

m0 = m[0]
m1 = bytes_to_long(m[1])
m2 = m[2].hex()
m3 = b64encode(m[3])

print(f'm0 = {m0}\nm1 = {m1}\nm2 = {m2}\nm3 = {m3}')"""

照着敲就好了

from Crypto.Util.number import long_to_bytes
from base64 import b64decode
m0 = b'0xGame{73d7'
m1 = 60928972245886112747629873
m2 = "3165662d393339332d3034"
m3 = b'N2YwZTdjNGRlMX0='

print(m0+long_to_bytes(m1)+bytes.fromhex(m2)+b64decode(m3))
# b'0xGame{73d72f64-7656-11ef-9393-047f0e7c4de1}'

Code-Vigenere

from secret import flag
from os import urandom
from base64 import b64encode

def Encrypt(msg, key):
    Lenth = len(key)
    result = ''

    upper_base = ord('A')
    lower_base = ord('a')
    KEY = [ord(key.upper()[_]) - upper_base for _ in range(Lenth)]

    index = 0
    for m in msg:
        tmp_key = KEY[index%Lenth] 
        if not m.isalpha():
            result += m
            continue

        if m.isupper(): 
            result += chr(upper_base + (ord(m) - upper_base + tmp_key) % 26)
        else: 
            result += chr(lower_base + (ord(m) - lower_base + tmp_key) % 26)
        index += 1
    return result

key = b64encode(urandom(6))[:5].decode()
print(Encrypt(flag,key))

利用密文前5个字母，配合已知flag头为0xGame可以猜测出密钥

因为最后加密模了26，所以只要在26的范围内爆破一下就好了。

后面解密就把+tmp_key改成-tmp_key就好了。

c="0lCcop{oyd94092-g8mq-4963-88b6-4helrxdhm6q7}"

m="0xGame"
key=[]
upper_base = ord('A')
lower_base = ord('a')
for i in range(1,len(m)):
    for tmp_key in range(26):
        if m[i].isupper(): 
            ci = upper_base + (ord(m[i]) - upper_base + tmp_key) % 26
        else: 
            ci = lower_base + (ord(m[i]) - lower_base + tmp_key) % 26
        if ci==ord(c[i]):
            key.append(tmp_key)
            break
print(key)

index=0
flag=""
for m in c:
    tmp_key=key[index%len(key)]
    if not m.isalpha():
        flag += m
        continue

    if m.isupper(): 
        flag += chr(upper_base + (ord(m) - upper_base - tmp_key) % 26)
    else: 
        flag += chr(lower_base + (ord(m) - lower_base - tmp_key) % 26)
    index += 1
print(flag)
# 0xGame{acb94092-e8bc-4963-88f6-4fcadbbfb6c7}

Number-Theory-CRT

from Crypto.Util.number import bytes_to_long, getPrime
from hashlib import md5
from random import randint
from gmpy2 import invert,gcd

#Hash Function:
def MD5(m):return md5(str(m).encode()).hexdigest()

#RSA AlgorithmParameter Generation Function:
def KeyGen():
	Factor_BitLength = 30
	q = getPrime(Factor_BitLength)
	p = getPrime(Factor_BitLength)
	N = p * q
	#Euler's totient function:
	phi = (p-1) * (q-1)

	#Generate Keys:
	e = randint(1,phi)

	#Generate Result:
	Pub_Key = (N,e)
	return Pub_Key

Pub = KeyGen()

N = Pub[0]
e = Pub[1]

#RSA Encrypt:
m = randint(1,N)
c = pow(m,e,N)

print(f'Pub_Key = {Pub}')
print(f'Encrypt_msg = {c}')

网站分解出p,q

发现e和phi不互素，gcd为2，可以直接求出\(m^2\mod n\)

之后发现p%4=3,q%4=1

对\(m^2\mod p\)使用rabin解密

然后\(m^2\mod q\)使用cipoll算法

之后枚举crt一下就好了

cipoll算法我参考的是：

https://blog.csdn.net/doyouseeman/article/details/52033204
https://unborracho.github.io/2023/04/20/二次剩余/index.html#:~:text=cipoll

from Crypto.Util.number import *
from hashlib import md5
from gmpy2 import *
from sympy.ntheory.modular import crt

def MD5(m):return md5(str(m).encode()).hexdigest()

Pub_Key = (1022053332886345327, 294200073186305890)
Encrypt_msg = 107033510346108389

# factordb
p=970868179
q=1052721013
phi=(p-1)*(q-1)
g=gcd(Pub_Key[1],phi)
gd=invert(Pub_Key[1]//g,phi)

mg=pow(Encrypt_msg,gd,Pub_Key[0])

#rabin
m1 = pow(mg, (p + 1) // 4, p)
m2 = p-pow(mg, (p + 1) // 4, p)
mp=[m1,m2]

#cipoll
def square_root_of_quadratic_residue(n, modulo):
    """Square root of quadratic residue

    Solve the square root of quadratic residue using Cipolla's algorithm with Legendre symbol
    Returns:
        int -- if n is a quadratic residue,
                   return x, such that x^{2} = n (mod modulo)
               otherwise, return -1
    """
    if modulo == 2:
        return 1
    if n % modulo == 0:
        return 0
    Legendre = lambda n: pow(n, modulo - 1 >> 1, modulo)
    if Legendre(n) == modulo - 1:
        return -1
    t = 0
    while Legendre(t ** 2 - n) != modulo - 1:
        t += 1
    w = (t ** 2 - n) % modulo
    return (generate_quadratic_field(w, modulo)(t, 1) ** (modulo + 1 >> 1)).x

def generate_quadratic_field(d, modulo=0):
    """Generate quadratic field number class

    Returns:
        class -- quadratic field number class
    """
    assert (isinstance(modulo, int) and modulo >= 0)

    class QuadraticFieldNumber:
        def __init__(self, x, y):
            self.x = x % modulo
            self.y = y % modulo

        def __mul__(self, another):
            x = self.x * another.x + d * self.y * another.y
            y = self.x * another.y + self.y * another.x
            return self.__class__(x, y)

        def __pow__(self, exponent):
            result = self.__class__(1, 0)
            if exponent:
                temporary = self.__class__(self.x, self.y)
                while exponent:
                    if exponent & 1:
                        result *= temporary
                    temporary *= temporary
                    exponent >>= 1
            return result

        def __str__(self):
            return '({}, {} \\sqrt({}))'.format(self.x, self.y, d)

    return QuadraticFieldNumber

mq=(square_root_of_quadratic_residue(mg,q))
mq=[mq,q-mq]

for i in mp:
	for j in mq:
		m=int(crt([p,q],[i,j])[0])
		flag = '0xGame{'+ MD5(m) +'}'
		print(m,flag)
#759871216848924391 0xGame{127016d0be858ef48a99723710ad4d49}