DragonKnightCTF 2024
misc
签到
用stegsolve发现二维码,扫码关注 中学生CTF 发送 Dragon Knight 2024 即可获得flag
神秘文字
一开始想着埃及文,找了半天发现很多都没有对应的字符,都开始摆了。
但是,当我发给gpt后,发现是js混淆类的
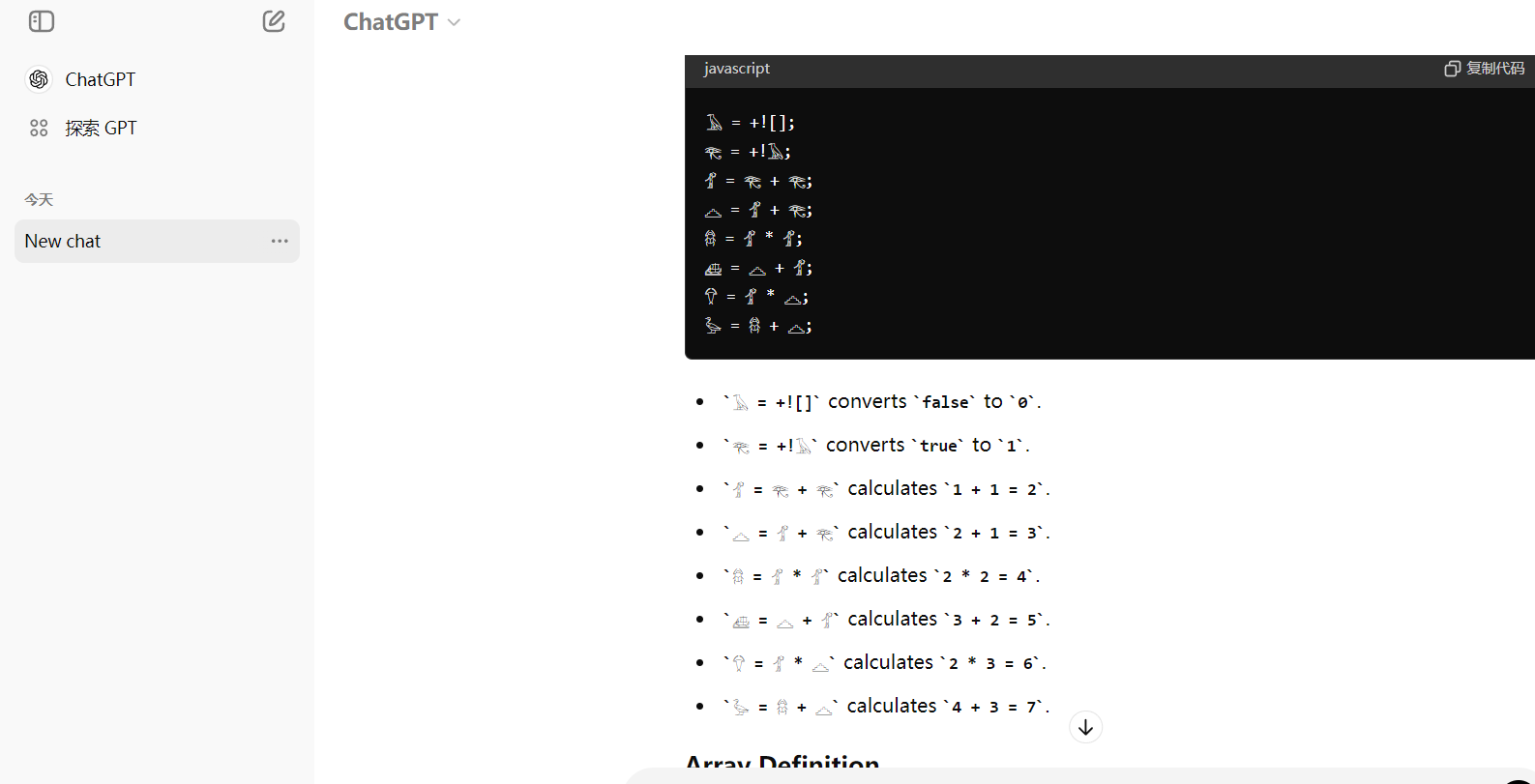
直接运行就拿到了压缩包密码了,然后解压就是flag
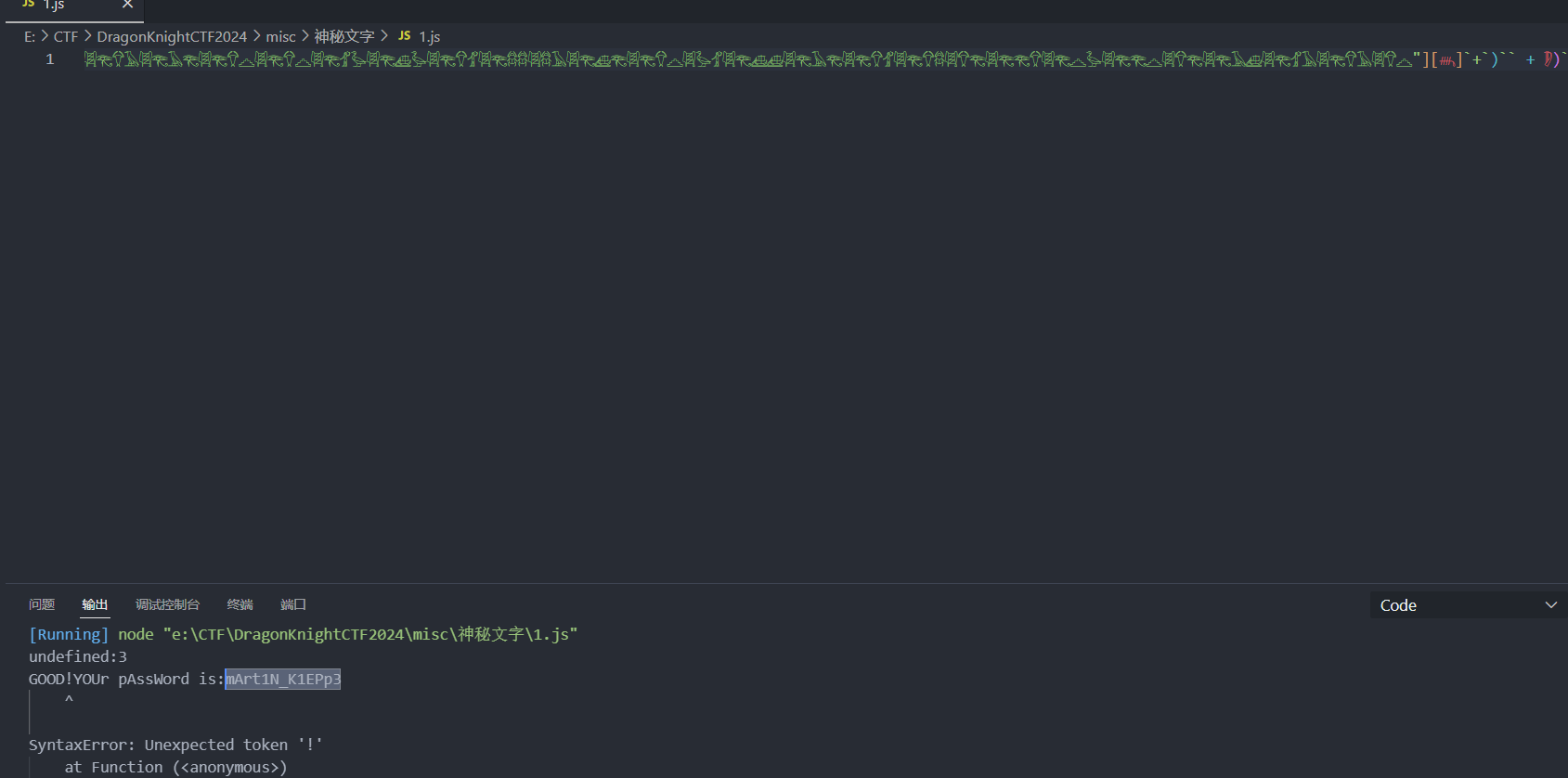
crypto
签到
分析之后是每次进行了两次普通的LCG,但其实没有影响
Xn+1=a2*Xn+a*b+b mod m
还是把每个部分当成一个整体计算就可以了
from Crypto.Util.number import *
"""m = b'flag{********}'
a = getPrime(247)
b = getPrime(247)
n = getPrime(247)
seed = bytes_to_long(m)
class LCG:
def __init__(self, seed, a, b, m):
self.seed = seed
self.a = a
self.b = b
self.m = m
def generate(self):
self.seed = (self.a * self.seed + self.b) % self.m
self.seed = (self.a * self.seed + self.b) % self.m
return self.seed
seed = bytes_to_long(m)
output = LCG(seed,a,b,n)
for i in range(getPrime(16)):
output.generate()
print(output.generate())
print(output.generate())
print(output.generate())
print(output.generate())
print(output.generate())"""
'''
5944442525761903973219225838876172353829065175803203250803344015146870499
141002272698398325287408425994092371191022957387708398440724215884974524650
42216026849704835847606250691811468183437263898865832489347515649912153042
67696624031762373831757634064133996220332196053248058707361437259689848885
19724224939085795542564952999993739673429585489399516522926780014664745253
'''
from gmpy2 import *
s = [5944442525761903973219225838876172353829065175803203250803344015146870499,141002272698398325287408425994092371191022957387708398440724215884974524650,42216026849704835847606250691811468183437263898865832489347515649912153042,67696624031762373831757634064133996220332196053248058707361437259689848885,19724224939085795542564952999993739673429585489399516522926780014664745253]
t = []
l=len(s)
for i in range(1,l):
t.append(s[i]-s[i-1])
all_n = []
for i in range(1,l-3):
all_n.append(gcd((t[i+1]*t[i-1]-t[i]*t[i]), (t[i+2]*t[i]-t[i+1]*t[i+1])))
for n in all_n:
n=abs(n)
if n==1:
continue
a=(s[2]-s[1])*invert((s[1]-s[0]),n)%n
ani=invert(a,n)
b=(s[1]-a*s[0])%n
seed = (ani*(s[0]-b))%n
for i in range(2**16):
if b'flag' in long_to_bytes(seed):
print(long_to_bytes(seed))
seed = (ani*(seed-b))%n
#b'flag{Hello_CTF}'
MatrixRSA_Revenge
之前H&NCTF中有一题一样的,具体步骤跟求RSA相同
只有求phin时不同,下面是参考论文
关于phin的问题,之前H&NCTF中 糖醋小鸡块师傅有解答一部分
具体是对于求phin其实并没有那么严格
因此,该题可以用上面那题的代码也可以实现
EXP:
#sagemath
from Crypto.Util.number import *
import os
from gmpy2 import *
"""flag = b"DRKCTF{??????????????}" + os.urandom(212)
p = getPrime(120)
q = getPrime(120)
print(f"p = {p}")
print(f"q = {q}")
part = [bytes_to_long(flag[16*i:16*(i+1)]) for i in range(16)]
M = Matrix(Zmod(n),[
[part[4*i+j] for j in range(4)] for i in range(4)
])
e = 65537
C = M ** e
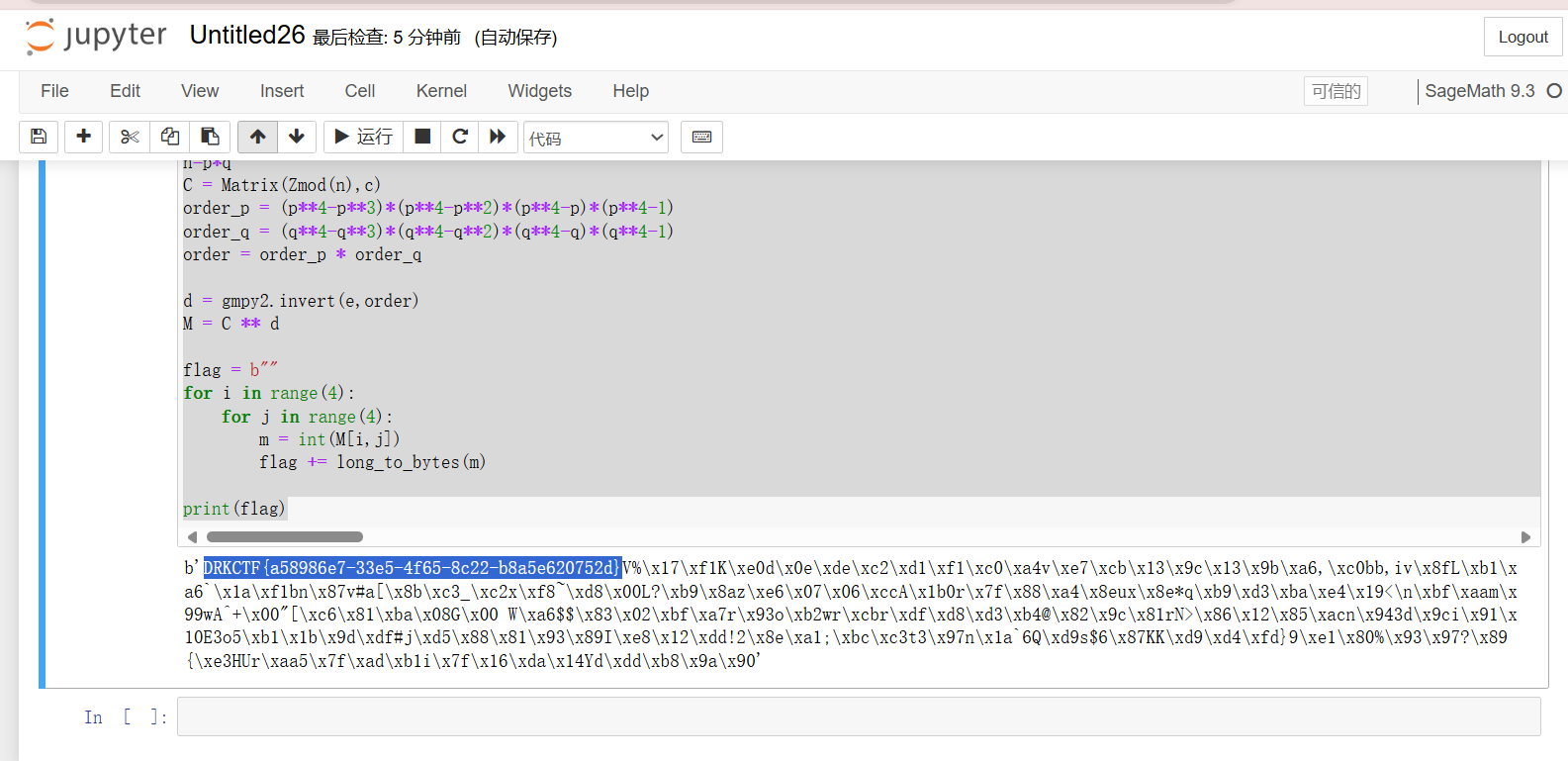
print(f"C = {list(C)}")"""
p = 724011645798721468405549293573288113
q = 712853480230590736297703668944546433
c = [(354904294318305224658454053059339790915904962123902870614765704810196137, 307912599668649689143528844269686459695648563337814923172488152872006235, 143644686443811064172873392982322248654471792394264352463341325181752577, 22995887787365556743279529792687264972121816670422146768160153217903088), (111349308911096779758451570594323566987628804920420784718347230085486245, 370237591900013263581099395076767089468466012835217658851568690263421449, 305451886364184428434479088589515273362629589399867618474106045683764897, 454103583344277343974714791669312753685583930212748198341578178464249150), (168497521640129742759262423369385500102664740971338844248603058993335309, 228941893018899960301839898935872289351667488000643221589230804176281482, 340080333594340128998141220817079770261711483018587969623825086357581002, 122922413789905368029659916865893297311475500951645918611759627764993518), (10332477229415731242316540110058798318207430965033579181240340751539101, 238172263316130590821973648893483382211906906298557131324791759298887701, 487586702165464601760230182019344052665496627253691596871783460314632260, 12238020921585443139790088280608644406695242899000592355653073240122626)]
e = 65537
n=p*q
C = Matrix(Zmod(n),c)
order_p = (p**4-p**3)*(p**4-p**2)*(p**4-p)*(p**4-1)
order_q = (q**4-q**3)*(q**4-q**2)*(q**4-q)*(q**4-1)
order = order_p * order_q
d = gmpy2.invert(e,order)
M = C ** d
flag = b""
for i in range(4):
for j in range(4):
m = int(M[i,j])
flag += long_to_bytes(m)
print(flag)
EzDES
不是哥们,我都没想到能出来
太抽象了把
from Crypto.Cipher import DES
from Crypto.Util.Padding import pad
from Crypto.Util.number import *
"""from secret import flag,key
key = bytes.fromhex(key)
des = DES.new(key, DES.MODE_ECB)
enc = des.encrypt(pad(flag,64))
print(enc)
"""
a=b't\xe4f\x19\xc6\xef\xaaL\xc3R}\x08;K\xc9\x88\xa6|\nF\xc3\x12h\xcd\xd3x\xc3(\x91\x08\x841\xca\x8b\xc1\x94\xb5\x9f[\xcd\xc6\x9f\xf9\xf6\xca\xf5\x1a\xda\x16\xcf\x89\x154\xa1\xfe\xc5\x16\xcf\x89\x154\xa1\xfe\xc5'
i=1<<56
while 1:
key=long_to_bytes(i)
des = DES.new(key, DES.MODE_ECB)
dec = des.decrypt(a)
if b'DRKCTF' in dec:
print(dec)
break
i=i+1
if i>=(1<<64):
print("no")
break
#b'DRKCTF{We4k_K3y_1s_V3ry_D4nger0us_In_DES}\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17\x17'
MyEncrypto
首先利用z3解方程求出r,然后就是简单的RSA求出P
from Crypto.Util.number import *
import random
"""def getMyPrime():
while True:
r = random.getrandbits(64)
_p = r**6 -3*r**5 - r**4 + r**2 - r - 6
_q = r**7 + 2*r**6 + r**5 + 4*r**4 + 7*r**2 + r + 4653
if isPrime(_p) and isPrime(_q):
return _p, _q
def enc(m, n):
return pow(m, 65537, n)
def LCG(s,a,b,n):
return (a*s + b) % n
flag=b'DRKCTF{******}'
seed = bytes_to_long(flag)
P = getPrime(512)
a = random.randrange(0,P)
b = random.randrange(0,P)
def Roll():
global seed
seed = LCG(seed,a,b,P)
return seed % 2**16
p, q = getMyPrime()
n = p * q
enc_P = enc(P, n)
print(f"n = {n}")
print(f"enc_P = {enc_P}")
out = []
for _ in range(40):
out.append(Roll())
print(f"a = {a}")
print(f"b = {b}")
print(f"out = {out}")"""
n = 17959692613208124553115435318871530105762927141420294800783695207170608966804977782615874404539156257549097962410144332053383210075663138848832474791712256427111304125146378883542387121684653496644116081809328796925343393644118376497507
enc_P = 17215745298239635988196009014709535403293865406390546681749129213899045156482782458937447412919331336842808052179915132663427715069134196783415529688715962754860563850858056507148936427379551986735103284388996678146580229028006898491552
a = 2759277675743644814124420138047586760905070650864591936190199977578763421196999718749092450720072564786874114432179104175692800471519816376692104515142375
b = 8111240578821759579875175166986910195923820191652867334412871591814076020421468033017946066268237980082938735686222173713853299600396887041341974719819186
out = [39566, 15295, 19818, 55685, 49100, 6517, 2675, 9567, 37243, 40312, 42906, 35874, 44178, 1256, 40298, 29149, 35721, 19886, 63020, 50116, 6844, 39897, 16134, 50218, 44609, 46188, 52712, 49903, 20933, 5441, 19411, 8330, 6904, 39350, 60853, 43446, 35910, 43728, 61533, 13757]
"""from z3 import *
r=Int('r')
s=Solver()
s.add(r<2**64,(r**6 -3*r**5 - r**4 + r**2 - r - 6)*(r**7 + 2*r**6 + r**5 + 4*r**4 + 7*r**2 + r + 4653)==n)
s.check()
m=s.model()
print(m[m.decls()[0]])"""
from gmpy2 import *
r=1248775963213848425
p = r**6 -3*r**5 - r**4 + r**2 - r - 6
q = r**7 + 2*r**6 + r**5 + 4*r**4 + 7*r**2 + r + 4653
e=65537
P=pow(enc_P,invert(e,(p-1)*(q-1)),n)
#10679387699123200522776360035184725927822172255453595568464894884736102462568579313264894449779104030120028056158023524486966766295648236135714849745610937
格密码我是一点没看懂,慢慢来学,但是找了类似的题
把这个例子EXP中的100换成2**16即可
#sagemath
from sage.all import *
from Crypto.Util.number import bytes_to_long, long_to_bytes
a = 2759277675743644814124420138047586760905070650864591936190199977578763421196999718749092450720072564786874114432179104175692800471519816376692104515142375
b = 8111240578821759579875175166986910195923820191652867334412871591814076020421468033017946066268237980082938735686222173713853299600396887041341974719819186
m = 10679387699123200522776360035184725927822172255453595568464894884736102462568579313264894449779104030120028056158023524486966766295648236135714849745610937
l = [0,39566, 15295, 19818, 55685, 49100, 6517, 2675, 9567, 37243, 40312, 42906, 35874, 44178, 1256, 40298, 29149, 35721, 19886, 63020, 50116, 6844, 39897, 16134, 50218, 44609, 46188, 52712, 49903, 20933, 5441, 19411, 8330, 6904, 39350, 60853, 43446, 35910, 43728, 61533, 13757]
A = [1]
B = [0]
for i in range(1, len(l)-1):
A.append(a*A[i-1] % m)
B.append((a*B[i-1]+(a*l[i]+b-l[i+1])*inverse_mod(2**16,m)) % m)
A = A[1:]
B = B[1:]
dim = len(l)
M = matrix(ZZ, dim, dim)
for i in range(dim-2):
M[i, i] = m
M[-2, i] = A[i]
M[-1, i] = B[i]
M[i, -2] = M[i, -1] = 0
M[-2,-2] = 1
M[-1,-1] = m//(2**16)
ll = M.LLL()[0]
l1 = ll[-2]
h1 = l[1]
s1 = l1*2**16+h1
#for s1=a*seed+b%m
seed = ((s1-b)*inverse_mod(a,m))%m
print(seed)
print(long_to_bytes(seed))
#2448362126058501250353008578968898134742331314317704567359511706590811819124428162365725464780212201207933
#b'DRKCTF{a57b63a6-ecf5-46d3-a501-2d359a4fd168}'
OSINT
羡慕群友每一天
谷歌识图,每个点进去看看,最后发现有个视频很像
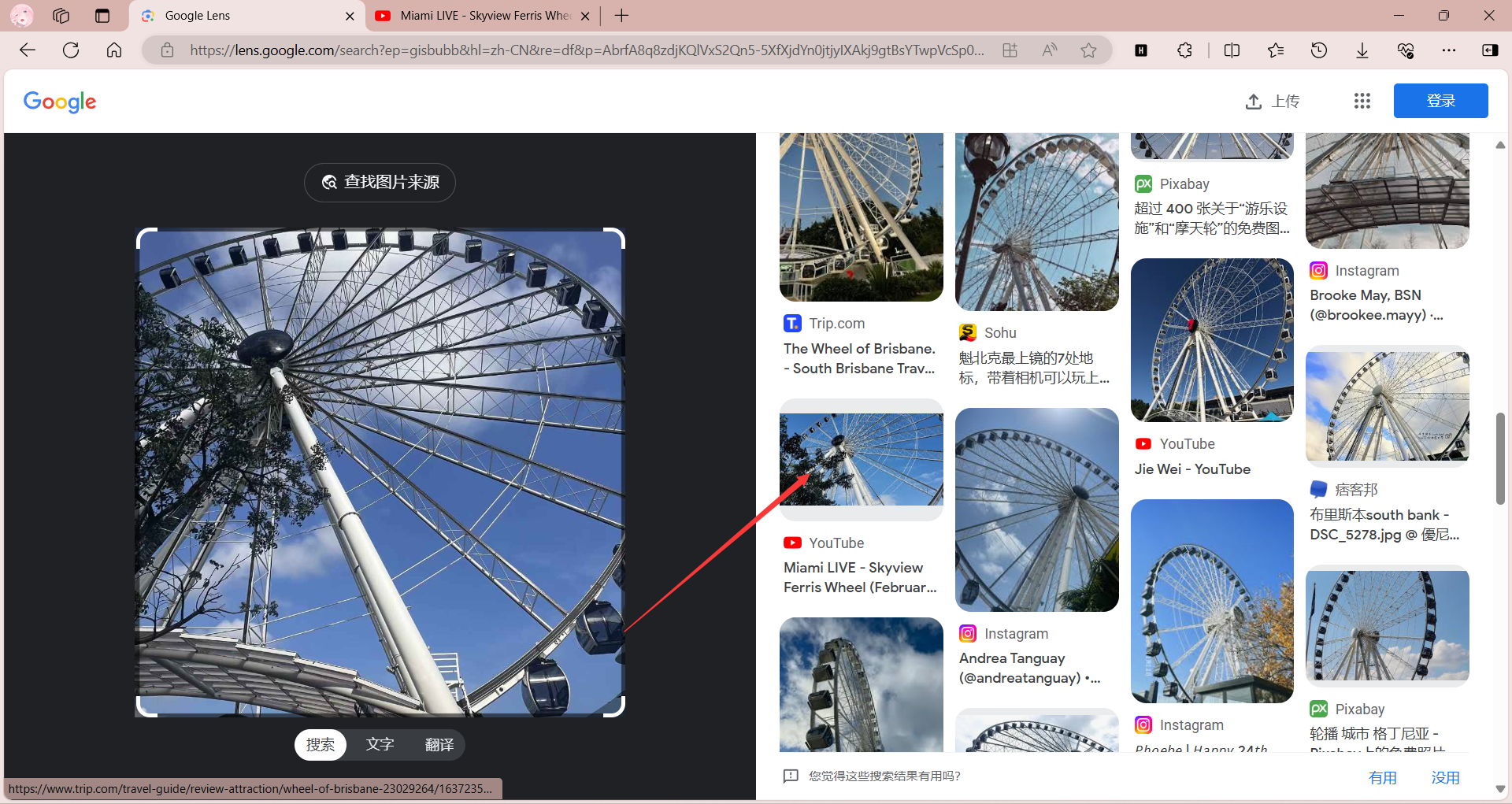
这里可以发现低下有一个锯齿状,旁边还有树
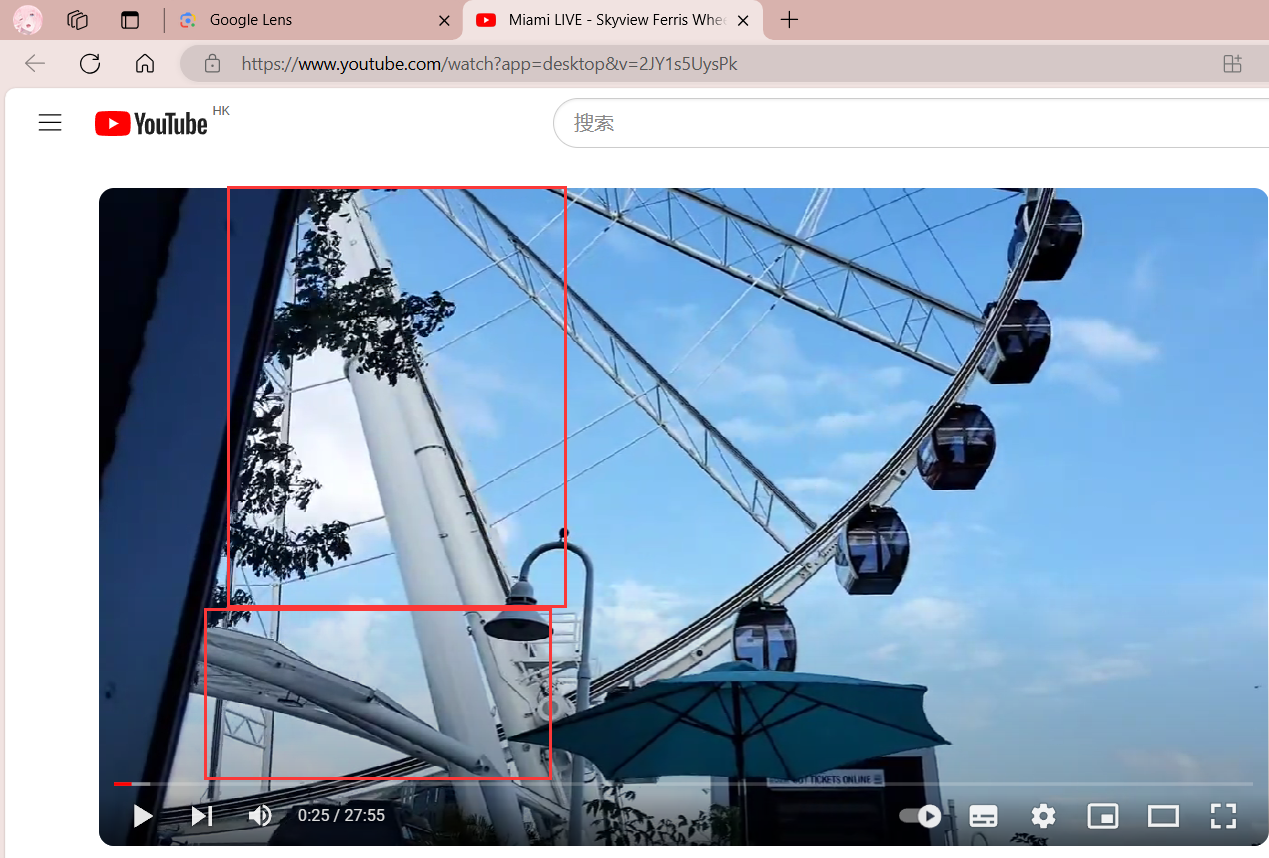
最后查找摩天轮的英文有点坑了
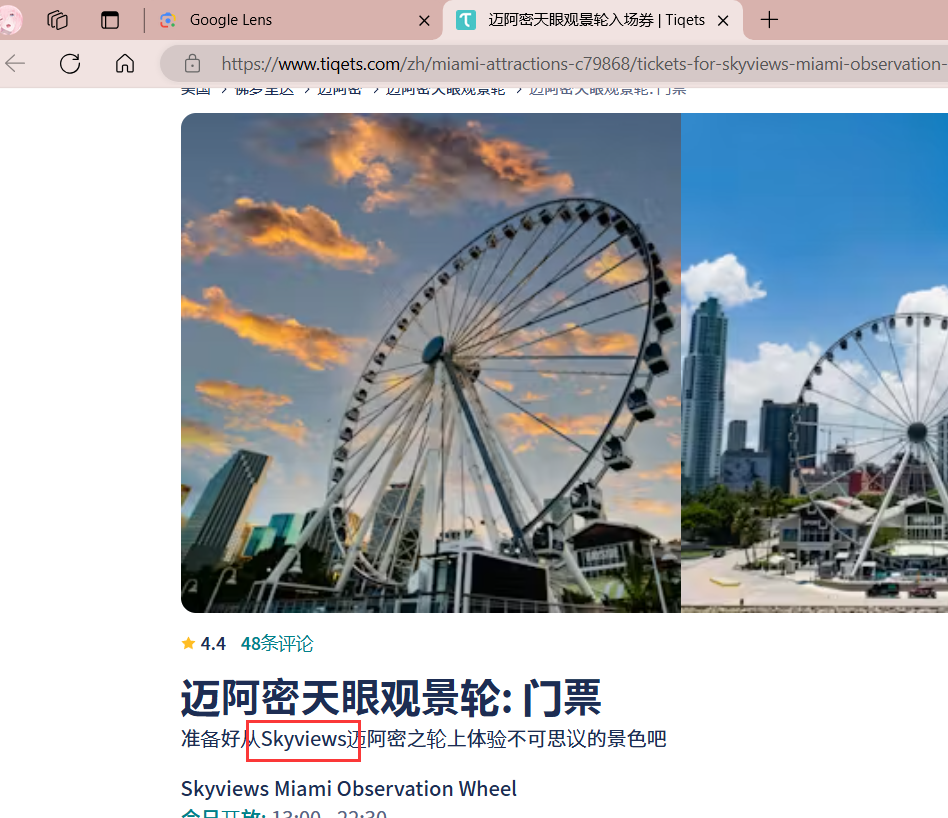
DRKCTF{美国-佛罗里达州-迈阿密市-Skyviews}



