在 Prim 算法中使用 pb_ds 堆优化

在 Prim 算法中使用 pb_ds 堆优化

Prim 算法用于求最小生成树（Minimum Spanning Tree，简称 MST），其本质是一种贪心的加点法。对于一个各点相互连通的无向图而言，Prim 算法的具体步骤如下：

令 \(G=(V,E)\) 表示原图，\(G'=(V',E')\) 表示 \(G\) 的最小生成树，\(dis_u\) 表示节点 \(u\) 到任意 \(v \in V'\) 的最小距离（初始化为 \(+\infty\)）。

1. 任取节点\(s \in V\)，令 \(dis_s=0\)；
2. 找到一个节点 \(u \in \complement_V V'\)，使得 \(dis_u\) 最小；
3. 将 \(u\) 加入 \(V'\)，\(dis_u\) 所代表的边加入 \(E'\)；
4. 对于任意边 \((u,v)\in \complement_E E'\)，令 \(dis_v=\min \{dis_v,w\}\)，其中 \(w\) 为边 \((u,v)\) 的权值；
5. 重复过程 2 到 过程 4，直到 \(V'=V\)。

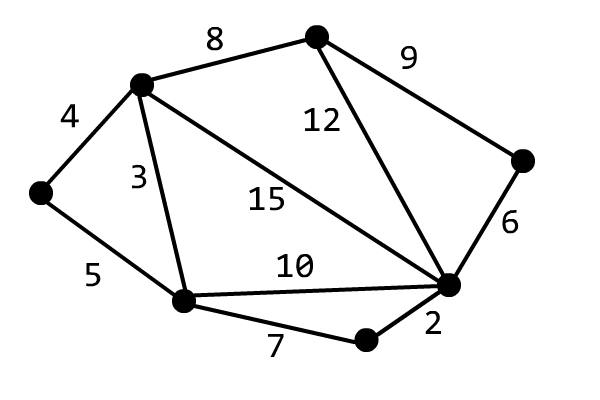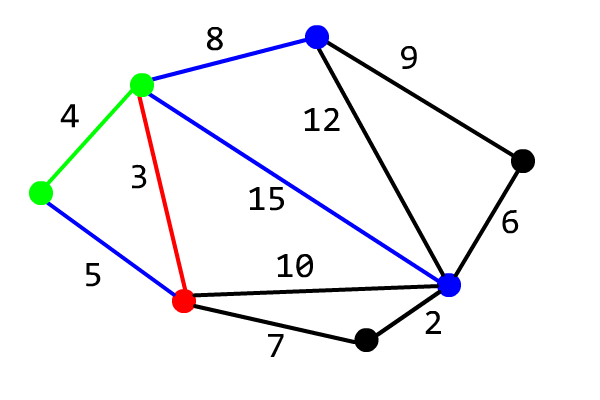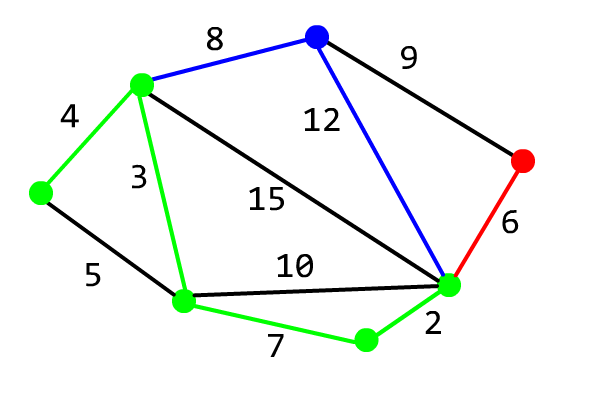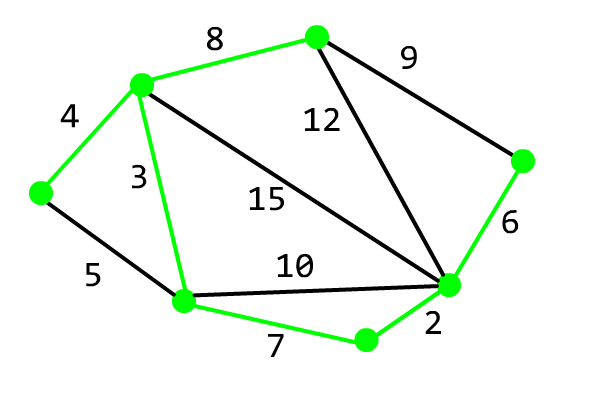
该算法的正确性证明可以参考 OI Wiki。

朴素的 Prim 算法时间复杂度为 \(O(n^2+m)\)，其中大部分时间都消耗在操作 2 上，可以考虑利用堆对其进行优化。用二叉堆等不支持 \(O(1)\) decrease-key 操作的堆优化后时间复杂度为 \(O((n+m)\log n)\)，用 Fibonacci 堆优化后的时间复杂度为 \(O(n \log n+m)\)（参考 OI Wiki）。相较于 Kruskal 算法，Prim 算法在 稠密图 上的效率更高。

Prim 算法中大量使用到 decrease-key 操作。在 OI 竞赛中，为节约时间，可以使用 C++ 标准库中封装好的数据结构代替手写堆。由于 std::priority_queue 不支持 decrease-key 操作，常常用 std::map 代替。实际上，std::set 内部实现是一棵常数较大的红黑树，这种用法显然会影响运行效率。鉴于当前 OI 竞赛中几乎全部采用 GNU 编译器，且 CCF 已经明确允许使用 pb_ds，我们可以使用 __gnu_pbds::priority_queue 作为堆来优化 Prim 算法，可以选择不同种类的堆作为内部实现，其中最快也是默认的是 配对堆（Pairing Heap）。具体使用方式见代码模板（P3366 【模板】最小生成树 - 洛谷，需要 C++14 标准）：

#include <bits/extc++.h>

using namespace std;
const int maxn = 5005;
const int inf = 0x3f3f3f3f;
int n, m;
vector<pair<int, int>> g[maxn];
__gnu_pbds::priority_queue<pair<int, int>, greater<>> heap;
__gnu_pbds::priority_queue<pair<int, int>, greater<>>::point_iterator p[maxn];  // dis[i] and iterator for decrease-key

int prim() {
    int ans = 0;
    p[1] = heap.push(make_pair(0, 1));
    for (int i = 2; i <= n; ++i)
        p[i] = heap.push(make_pair(inf, i));
    while (!heap.empty()) {
        if (heap.top().first == inf)
            return -1;
        int u = heap.top().second;
        ans += heap.top().first;
        heap.pop();
        p[u] = heap.end();
        for (auto& i : g[u])
            if (p[i.first] != heap.end() && i.second < p[i.first]->first)
                heap.modify(p[i.first], make_pair(i.second, i.first));
    }
    return ans;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> m;
    for (int i = 1; i <= m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        g[u].emplace_back(v, w);
        g[v].emplace_back(u, w);
    }
    int ans = prim();
    if (ans != -1)
        cout << ans << endl;
    else
        cout << "orz" << endl;
    return 0;
}

---

转载请注明出处。原文地址：https://www.cnblogs.com/na-sr/p/prim-pbds.html