Cryptohack的Adrien's Signs解题思路

题目如下：

 

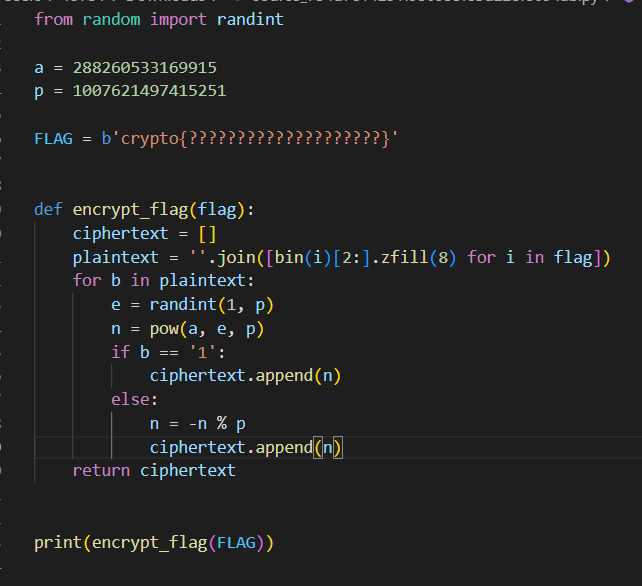
输出的结果：

 

 

 题目分析：

在原题的题目描述中并没有什么有用的消息，更多的信息是通过代码审计出来的。大致意思是，先把字节flag转换为二进制形式的字符串，然后判断字符串中每个字符，如果为1，则直接添加到cipertext列表中，否则对n 取负再求余，得到结果添加到cipertext列表中。

源码中给了a和p，根据前面知识，先计算一下勒让德符号(Legendre's Symbol)：(a / p) ≡ a(p-1)/2 mod p

 

a_p = pow(a, (p - 1) // 2, p)
print(a_p)

 

返回结果为：1

说明a 是二次剩余，a的幂也是二次剩余，原因由二次剩余性质得到，如下：

 

 

 Quadratic Residue，简称QR，中文称作二次剩余，则QNR 称作二次非剩余

所以 a^e 可看成 e 个 a 相乘，则  a^e 也是二次剩余

因为 b == ‘1’ 时是直接把 n 添加到 cipertext 列表中的，所以我们对 n 求勒让德符号，结果为 1 则说明 a^e 为二次剩余，满足上述条件，则 b = 1

勒让德符号服从如下关系：

<img src="https://img2022.cnblogs.com/blog/2842002/202207/2842002-20220707133427893-962023011.png" alt="" loading="lazy">

 

 否则 我们断言 n 不是二次剩余，返回的是 p - 1。原因是勒让德符号等于 -1 ，而pow函数是不会返回负数，则返回的是 p - 1

解题代码：

#coding:utf-8
result_list = [67594220461269, 501237540280788, 718316769824518, 296304224247167, 48290626940198, 30829701196032, 521453693392074, 840985324383794, 770420008897119, 745131486581197, 729163531979577, 334563813238599, 289746215495432, 538664937794468, 894085795317163, 983410189487558, 863330928724430, 996272871140947, 352175210511707, 306237700811584, 631393408838583, 589243747914057, 538776819034934, 365364592128161, 454970171810424, 986711310037393, 657756453404881, 388329936724352, 90991447679370, 714742162831112, 62293519842555, 653941126489711, 448552658212336, 970169071154259, 339472870407614, 406225588145372, 205721593331090, 926225022409823, 904451547059845, 789074084078342, 886420071481685, 796827329208633, 433047156347276, 21271315846750, 719248860593631, 534059295222748, 879864647580512, 918055794962142, 635545050939893, 319549343320339, 93008646178282, 926080110625306, 385476640825005, 483740420173050, 866208659796189, 883359067574584, 913405110264883, 898864873510337, 208598541987988, 23412800024088, 911541450703474, 57446699305445, 513296484586451, 180356843554043, 756391301483653, 823695939808936, 452898981558365, 383286682802447, 381394258915860, 385482809649632, 357950424436020, 212891024562585, 906036654538589, 706766032862393, 500658491083279, 134746243085697, 240386541491998, 850341345692155, 826490944132718, 329513332018620, 41046816597282, 396581286424992, 488863267297267, 92023040998362, 529684488438507, 925328511390026, 524897846090435, 413156582909097, 840524616502482, 325719016994120, 402494835113608, 145033960690364, 43932113323388, 683561775499473, 434510534220939, 92584300328516, 763767269974656, 289837041593468, 11468527450938, 628247946152943, 8844724571683, 813851806959975, 72001988637120, 875394575395153, 70667866716476, 75304931994100, 226809172374264, 767059176444181, 45462007920789, 472607315695803, 325973946551448, 64200767729194, 534886246409921, 950408390792175, 492288777130394, 226746605380806, 944479111810431, 776057001143579, 658971626589122, 231918349590349, 699710172246548, 122457405264610, 643115611310737, 999072890586878, 203230862786955, 348112034218733, 240143417330886, 927148962961842, 661569511006072, 190334725550806, 763365444730995, 516228913786395, 846501182194443, 741210200995504, 511935604454925, 687689993302203, 631038090127480, 961606522916414, 138550017953034, 932105540686829, 215285284639233, 772628158955819, 496858298527292, 730971468815108, 896733219370353, 967083685727881, 607660822695530, 650953466617730, 133773994258132, 623283311953090, 436380836970128, 237114930094468, 115451711811481, 674593269112948, 140400921371770, 659335660634071, 536749311958781, 854645598266824, 303305169095255, 91430489108219, 573739385205188, 400604977158702, 728593782212529, 807432219147040, 893541884126828, 183964371201281, 422680633277230, 218817645778789, 313025293025224, 657253930848472, 747562211812373, 83456701182914, 470417289614736, 641146659305859, 468130225316006, 46960547227850, 875638267674897, 662661765336441, 186533085001285, 743250648436106, 451414956181714, 527954145201673, 922589993405001, 242119479617901, 865476357142231, 988987578447349, 430198555146088, 477890180119931, 844464003254807, 503374203275928, 775374254241792, 346653210679737, 789242808338116, 48503976498612, 604300186163323, 475930096252359, 860836853339514, 994513691290102, 591343659366796, 944852018048514, 82396968629164, 152776642436549, 916070996204621, 305574094667054, 981194179562189, 126174175810273, 55636640522694, 44670495393401, 74724541586529, 988608465654705, 870533906709633, 374564052429787, 486493568142979, 469485372072295, 221153171135022, 289713227465073, 952450431038075, 107298466441025, 938262809228861, 253919870663003, 835790485199226, 655456538877798, 595464842927075, 191621819564547]
a = 288260533169915
p = 1007621497415251

#计算勒让德符号
a_p = pow(a, (p - 1) // 2, p)
print(a_p)

# print(len(result_list))  224
plaintext = ''
for m in result_list:
    L = pow(m, (p - 1) // 2, p)
    # print(L)
    if L == 1:
        plaintext += '1'
    else:
        assert L == p - 1
        plaintext += '0'
print(plaintext)

flag = ''
for i in range(0, len(plaintext), 8):
    flag += chr(int(plaintext[i: i+8], 2))
print(flag)

总结：

勒让德符号可以用来快速判断一个数是不是二次剩余，当模数p 满足 模 4 余 3 时，还可以推出 (a^(p+1)/4 )²  ≡ a mod p 然后计算出 x² ≡ a mod p 中的x。