使用初中数学知识解RSA中两个素数存在线性关系

　　题目如下：

 

 

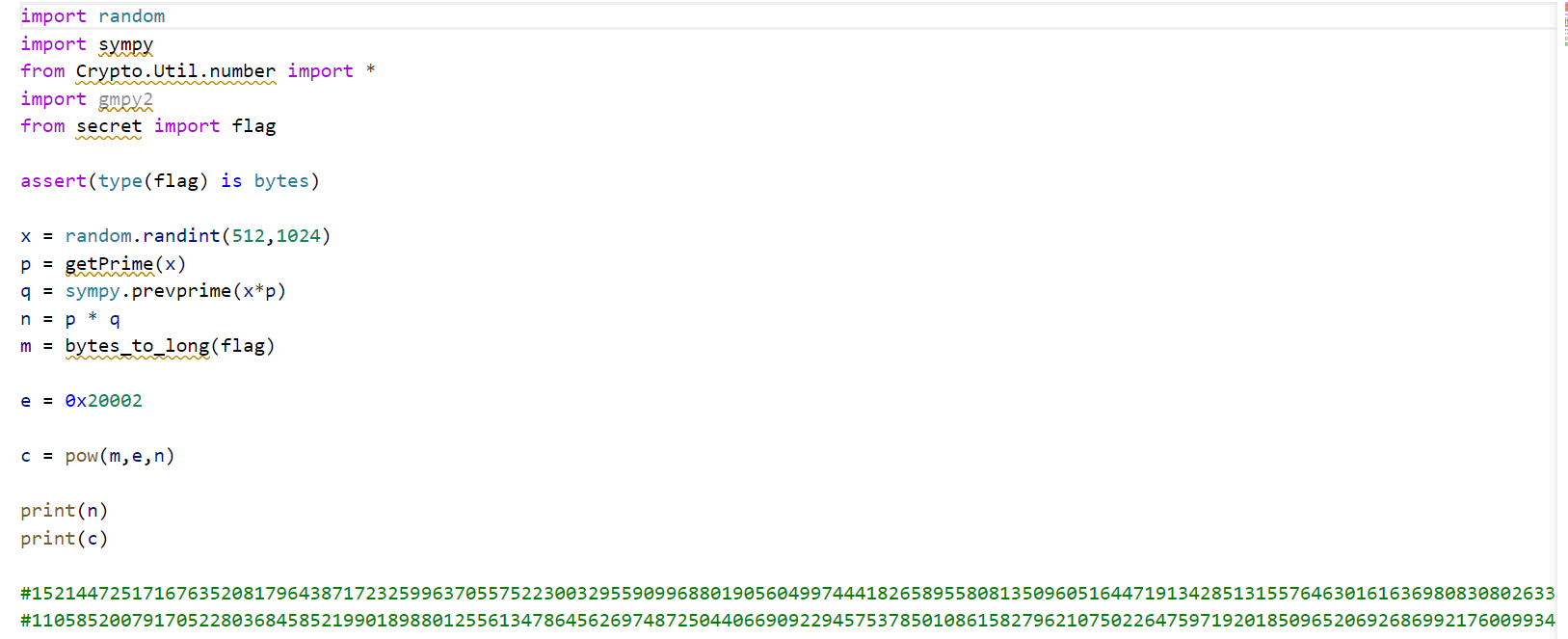
 题目中给了

n=

15214472517167635208179643871723259963705575223003295590996880190560499744418265895580813509605164471913428513155764630161636980830802633813663336583213161569538178508437359943631196481047739347775324187472085993738794470299908710911049348940248532805473566951285681866468589043457843762688499849012440295414493451692467370543822040652333188332816025075165979672831581290945925240985893490532001382605626325382054628858274579650347717335461976163004389030535919832078653634505987851574185666635841464028165894065757887647087214520446546500620861128042817428764084656276550191632918086102769087568522630555195097

c=

11058520079170522803684585219901898801255613478645626974872504406690922945753785010861582796210750226475971920185096520692686992176009934573619610958733046237941697968314511032451851585467734569392407182980753533348751810814013718365754750869633257153873276933960267067855974698884842720285929150910465894787273762026450256965090665900254208885227595964548981953518254550953773629567607146974719685702329042657032685765607803435883527947475703743642842955033421775334843375224801155478219009956642226332623779306451050115135524258410411580785604692272741152498796424309784159909128642849761091942473987146661728

e = 0x20002

解题思路：

题目给了n，c，e。已知密文解明文，解明文需要知道私钥，私钥由n和d组成，所以要知道d，解出d需要知道phi，而phi = (p -1) * (q -1 )，所以需要知道p和q，而p *q =n。所以直接暴力破解p和q，结果跑了一下午工具yafu，没出来，这不G了？分析py文件：x值的范围为512到1024，而p是等于2的x次方前的素数，q等于x*p的前一个素数，这里就假设一个k（为什么要假设k后面总结会说），使得p + k = x *p。所以思路就来了，先写解出p和q，根据题目的hint（两个素数总是很接近），我们知道k的范围比较小。所以脚本编写如下：

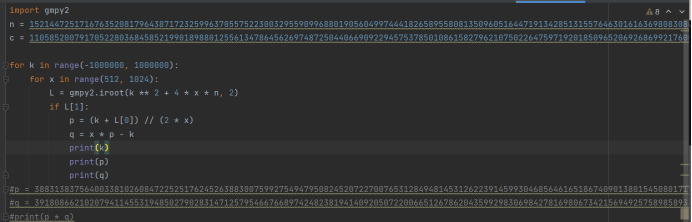
解出p和q，于是就可以解出d，然后就能知道明文，脚本如下：

 

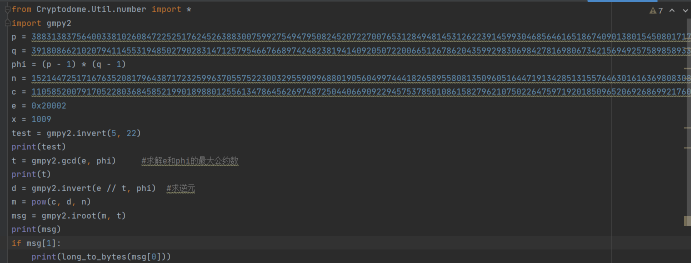
得到flag

 

一开始按照rsa正常解法得不出答案，后来发现e和phi的最大公约数为2，和rsa中规定不一样，于是需要用e除于t

　　总结：

如果在很大的情况下，无法直接对n分解出p和q，可根据题目找出p和q的线性关系，然后和p*q=n联立，可推出一元二次方程，根据求根公式即可解出p和q。如果存在不确定的情况，如题中x，for循环暴力破解即可。在标准rsa加密中，取的e要与phi互素（即两者最大公约数为1），题中进行了变形，两者最大公约数变成了2，所以在求d时需要e除于t。invert方法，就是对公式：ed ≡ 1(mod phi)求解d。还有一个求逆元的方法gcdext，它返回类型为元组，元组有3个值。它是对公式：ed ≡ 1(mod phi)  变形得到：ex + phi y = gcd（1）求解， 返回的3个值分别对应gcd，x，y。